基于Python程序設計的PMSM氣隙磁密分析

杜曉彬，黃開勝，蔡黎明

(1.廣東工業大學，廣州 510006;2.寧波供電局，寧波 315000)

0 引 言

隨著永磁材料性能的提高，以及電機設計和控制技術的提升，永磁電機應用范圍逐漸廣泛。其中，永磁同步電動機(以下簡稱PMSM)具有體積小、結構簡單、功率密度高的特點，被大量應用于生產實踐中[1]。ANSYS有限元仿真采用有限元離散形式，將電磁場計算轉化為矩陣求解，保證了計算的準確性和快捷性，通常采用ANSYS有限元仿真軟件對電機進行仿真計算以及設計[2]。它提供的快速傅里葉分解工具可以對PMSM氣隙磁密徑向分布進行快速分析，為用戶提供了方便。然而，進行快速傅里葉分解分析的結果可能會出現低次的諧波幅值比基波幅值大的情況，影響直觀判斷[3-4]，因此有必要開發設計軟件對FFT分析數據進行后處理，以直觀的圖表形式展現傅里葉分析的結果。

Python語言是一種功能強大的開源編程語言，相對于C語言和Java，VB等其他編程語言，Python可以通過錄入、調試更加少的代碼來實現相同的功能，而且具有其他語言沒有的強大的可移植性，可以實現在各個平臺直接復制使用[5]。本文的程序開發直接基于Python，以實現更加廣泛的使用。

本文以一臺48槽8極表貼式磁鋼的PMSM為例，應用Python語言進行程序設計，驗證了程序的正確性，研究了極弧系數對電機氣隙徑向磁密諧波畸變率的影響。

1 PMSM的氣隙磁場諧波分析

根據PMSM的原理，當電機通以對稱的m相交流電流，定子在氣隙中產生基波磁動勢以及一系列不同次數、幅值以及轉速的諧波磁動勢[6-8]。轉子磁鋼則在氣隙中產生基波磁動勢和一系列的諧波磁動勢。當定子上開槽，轉子磁鋼為表貼式時，氣隙磁導除了平均磁導，還有一系列的磁導諧波分量，定轉子磁動勢以及氣隙磁導相互作用產生了氣隙磁場。

PMSM氣隙中基波磁動勢與平均氣隙磁導相互作用，產生基波磁場bp=Bpcos(pθ1-ω1t)，p為電機極對數，ω1為電流的角頻率，θ1為定子空間的圓周角坐標。可以看出，基波的極對數為p。

2 有限元仿真和Python程序設計

2.1 ANSYS-Maxwell 2D分析氣隙磁場諧波

在PMSM中，電機的徑向氣隙磁場Br(θ,t)是沿著氣隙圓周分布的，它是時間與位置的函數，可以在電機氣隙中取一個固定時間點，并取沿著氣隙一周的路徑進行計算。

ANSYS-Maxwell 2D仿真軟件計算中，氣隙徑向磁密表達式：

Br=BXcosθ+BYsinθ

(1)

式中:BX為磁密沿著x軸的分量;BY為磁密沿著y軸的分量。根據式(1)，沿著該圓周可以繪制出橫坐標為空間位置，縱坐標為徑向磁密的波形圖。一般在工程技術上取該圓周半徑為定子內徑與轉子外徑的均值的一半，即：

(2)

由ANSYS-Maxwell 2D提供了對波形圖進行快速傅里葉分解的工具FFT，可以將Br波形圖分解為各次諧波以及對應的磁密諧波幅值大小，并表示為橫坐標為空間位置d，縱坐標為諧波幅值的傅里葉分解圖。其中，空間位置所對應的諧波極對數以及次數分別是：

(3)

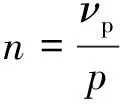
(4)

式中:vp為諧波極對數;n為諧波次數。當v為分數時，諧波為間諧波；當n為整數時，諧波為整數次諧波。

2.2 Python程序設計

為了簡化對ANSYS-Maxwell 2D快速傅里葉分析的數據處理，以直觀方便的形式從快速傅里葉分解的數據中篩選出用戶想要的結果，開發了本程序。程序基于語言簡潔的Python語言，以圖表的形式直觀地表示出各次諧波以及對應的諧波幅值，并快速計算出該波形的諧波畸變率，節省了對波形數據處理的時間。

2.2.1 Python程序設計內部流程

本程序設計的主要模塊如圖1所示。

圖1 Python設計程序的模塊示意圖

Python程序分析流程主要有3個模塊。第一模塊是對電機參數包括電機極對數p、定子內徑D1、轉子外徑D2的讀取和對氣隙徑向磁密快速傅里葉分解數據Data.csv的讀取。該模塊是程序分析的前提。第二模塊是將數據Data.csv中的D換算成諧波的次數 。通過用戶給出的諧波次數以及幅值的篩選條件，在大量的諧波中篩選出次數比較小、幅值比較大的諧波。該模塊是程序分析的主要部分。第三模塊是對處理完成的結果進行輸出，輸出內容為隙磁密諧波畸變率THD值以及諧波幅值柱狀圖。其中，程序的各個模塊具體流程敘述如下：。

(1)變量定義部分

程序包含了8個變量的定義，包括電機極對數p、定子內徑D1、轉子外徑D2、圓周半徑R、諧波極對數vp、諧波次數n、篩選諧波次數限定值nc、篩選諧波幅值限定值nm。其中，為了計算結果有較高的精度，將定子內外徑、圓周半徑、篩選諧波幅值限定值設定為float數據類型，而其他參數則設置為int數據類型。

(2)讀取Data.csv數據文件部分

該部分主要對應第一模塊第一步，對傅里葉分解的數據進行讀取工作，是程序分析的前提。由于從ANSYS-Maxwell 2D導出的原始數據文件Data.csv是以列表格式展現的，即第一列為空間位置數據，第二列為諧波幅值數據，故需要對數據文件進行讀取并對數據表格執行按列拆分功能。在程序中使用with open(file, 'r') as stream命令實現以上功能。

(3)讀取電機參數部分

該部分主要對應第一模塊第二步驟。主要讀取輸入的電機極對數p、定子內徑D1、轉子外徑D2。

(4)計算部分

該部分對應第二模塊的第一步驟。首先按照公式(2)計算該電機模型的氣隙圓周半徑R，其次按照式(3)與式(4)將讀取的空間位置數據依次換算成氣隙磁密諧波極對數和諧波次數。其中，對諧波極對數的次數取值為Fraction分數類型，以適用于分數槽集中繞組單相電機等其他機型運行過程中產生的間諧波。

(5)篩選諧波部分

該部分對應第二模塊的第二步驟。由用戶手動輸入篩選諧波的限制條件，即篩選諧波次數限定值nc和篩選諧波幅值限定值nm兩個條件，利用Python中filter函數，根據用戶需求按照諧波幅值以及諧波次數條件進行篩選。

(6)繪制諧波圖部分由以上第(4)部分的計算結果以及第(5)部分用戶的篩選結果，調用Matplotlib繪圖庫進行繪制bar圖，并以諧波次數為橫坐標，各次諧波幅值為縱坐標。

(7)計算THD部分

該部分對應第三模塊的第二步驟。在該部分定義函數THD(G)進行計算氣隙磁密諧波畸變率，其中，參數G為由第(5)篩選的諧波次數所對應的諧波幅值數組，并調用sqrt函數與sum函數完成計算功能。

為了進一步清晰地說明本程序的算法流程，給出程序流程圖如圖2所示，并包含了以上說明的三部分模塊的功能。

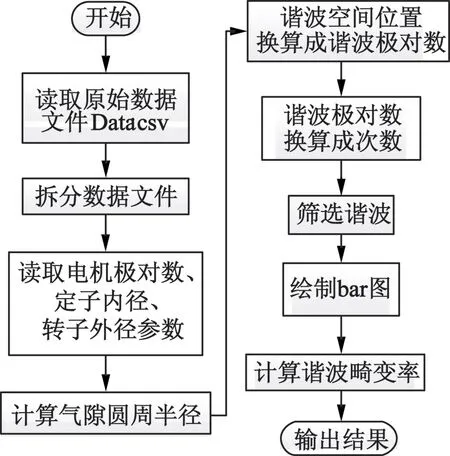
圖2 設計程序流程圖

2.2.2 ANSYS-Maxwell 2D與Python數據交互

本程序擁有友善的HCI界面，使用者可以在完全不考慮程序內部結構和內部特性的情況下，而直接使用它對數據進行分析處理，直接得出想要的結果。該程序與ANSYS-Maxwell 2D的交互過程如圖3所示。

圖3 數據交互傳遞過程

在ANSYS-Maxwell 2D仿真軟件建立PMSM有限元模型，進行仿真分析計算。計算完成后通過Draw circle命令繪制半徑為R的圓周，再通過Creat Transient Report命令繪制氣隙徑向磁場波形圖。完成之后通過Perform FFT on Report對波形圖傅里葉分解，得到關于空間位置和諧波幅值的傅里葉分解數據Data.csv。

打開Python分析程序Analyze.py，將Data.csv數據導入到分析程序中，輸入篩選的限制條件：諧波次數條件以及諧波幅值條件。該程序可以進行單一條件篩選或者兩個條件同時篩選，以滿足用戶的多種需求。對數據進行分析篩選完成以后，分析結果以橫坐標為篩選諧波的次數，縱坐標為篩選諧波的幅值的Bar Plot圖形呈現，并計算出該徑向諧波的畸變率THD。

3 有限元仿真分析與程序應用

以一臺8極48槽表貼式磁鋼的PMSM為例，仿真分析其額定負載時電樞磁場的徑向磁場以及額定負載時氣隙磁場的徑向磁場。

3.1 額定負載時電樞磁場徑向磁場諧波分析

鑒于需要分析定子繞組產生的徑向磁場磁密，故刪去ANSYS-Maxwell 2D電機模型中轉子上的磁鋼，然后進行仿真計算，單獨分析定子繞組在氣隙中產生的磁場。建立電機模型如圖4所示。

圖4 PMSM電樞磁場仿真模型

仿真結果通過ANSYS-Maxwell 2D自帶的FFT工具進行傅里葉分解，將分解結果數據保存為Data.csv文件。再通過Python程序分析，輸入篩選的限制條件：諧波次數為25及以下，諧波幅值大于0.005 T。并由Python程序直接繪出諧波圖如圖5所示，并計算出氣隙徑向磁密諧波畸變率的大小。

圖5 額定負載電樞磁場諧波

通過圖5可以看出，對定子繞組額定負載情況進行仿真，基波幅值最大為0.614T，諧波包含有5，7，11，13，17，19、25等次數。由于11，13次為一階齒諧波，諧波含量比較大。通過Python程序分析直接得出諧波此時畸變率為26.99%。符合上述關于PMSM的定子繞組磁場諧波的原理。

3.2 額定負載時氣隙徑向磁場諧波分析

在ANSYS-Maxwell 2D電機模型中，保留轉子上的磁鋼以及定子上的繞組，對氣隙中磁密進行仿真計算仍由Python設計程序進行分析，結果如圖6所示。

圖6 額定負載氣隙磁場諧波

由圖6可知，氣隙中的徑向磁密主要以奇數次磁密為主，其中，基波的幅值最大為0.957 T，諧波幅值以3，11，13次諧波幅值為主。諧波畸變率為16.56%。

通過以上仿真計算以及基于Python程序的對于數據的處理，驗證了程序的可靠性與實用性。

3.3 極弧系數對徑向磁密THD的影響

利用Python程序能快速地計算出諧波畸變率的特點，通過ANSYS-Maxwell 2D的參數化分析工具以及Python程序來進行仿真，分析極弧系數對徑向磁密THD的影響。仿真結果如圖7所示。

圖7 極弧系數對氣隙徑向磁密THD的影響

由圖7可知，當選擇不同的極弧系數時，諧波畸變率有不同的數值，且曲線呈現先下降后上升的趨勢，當選擇極弧系數為0.78時，THD有最小值14.81%。

由于當徑向氣隙磁密波形中的諧波含量越小，諧波畸變率會越小，諧波幅值越小。所以，在諧波磁場次數一定時，通過改變磁鋼的極弧系數來降低諧波幅值[9-11]。

由此可見，通過選擇恰當的極弧系數可以抑制諧波畸變率，使諧波更加趨近于正弦。

4 結 語

本文設計了一個基于Python的程序，用于對ANSYS-Maxwell 2D進行徑向磁密分析的數據進行后處理，它能準確快速地繪制出諧波圖形和計算出氣隙磁密THD值，節省了用戶的時間。通過仿真一臺48槽8極PMSM，驗證了程序的實用性和準確性。鑒于該程序能快速計算THD，利用該程序分析了不同極弧系數對徑向磁密諧波畸變率的影響。通過該方法，得出極弧系數對磁密諧波畸變率的影響規律。本文的程序設計思路以及方法為分析旋轉電機的氣隙徑向磁密提供了參考。

[1] 蔡黎明.永磁同步電動機電磁振動與噪聲的研究[D].廣州：廣東工業大學,2016.

[2] 趙博.Ansoft 12在工程電磁場中的應用[M].中國水利水電出版社,2010.

[3] 譚建成.永磁無刷直流電機技術[M].機械工業出版社,2011.

[4] 段世英.分數槽集中繞組永磁同步電機的若干問題研究[D].武漢：華中科技大學,2014.

[5] Python核心編程[M].機械工業出版社,2001.

[6] 黃國治,傅豐禮.中小旋轉電機設計手冊[M].中國電力出版社,2007.陳仲才.

[7] 王秀和.永磁電機[M].中國電力出版社,2011.

[8] 許實章.交流電機的繞組理論[M].北京.機械工業出版社,1985

[9] 肖慶優,黃開勝,陳文敏,等.一種確定永磁同步電動機最佳磁極偏移角度的方法[J].微特電機,2015,43(12):14-16.

[10] ZHENG P,ZHAO J,HAN J,et al.Optimization of the magnetic pole shape of a permanent-magnet synchronous motor[J].IEEE Transactions on Magnetics,2007,43(6):2531-2533.

[11] LI Y,XING J,WANG T,et al.Programmable design of magnet shape for permanent-magnet synchronous motors with sinusoidal back EMF waveforms[J].IEEE Transactions on Magnetics,2008,44(9):2163-2167.