例談幾種常用的整體性教學策略

蔣旭凱

摘要：數學知識的整體結構教學是指改變由局部到整體，將數學知識列為一個個知識點進行教學，依據數學知識之間的本質聯系和內在結構，以知識理解和存儲結構的特點進行數學知識的結構教學，在數學知識結構內部進行操作，強化通過一個既定的認知發展階段吸收新的知識的過程，使學生熟悉這些結構，并更好地掌握它們的復雜性，反過來又促進新知識的獲得，如此循環往復直至學習者的認知結構與知識結構取得一致。在此，筆者歸納了幾種常見的教學策略。

關鍵詞：數學教學；整體性教學；策略

中圖分類號：G633.6 文獻標識碼：A 文章編號：1992-7711（2017）03-0101

數學學習是建立和完善個體數學認知結構的過程，數學認知結構是由數學知識結構轉化而來的。如何通過數學識識結構的深度加工和數學教學內容的整體結構教學來改變教學內容點狀割裂狀態，揭示數學知識內在本質聯系與結構，構建數學知識網絡，通過整體結構教學引導學生發現結構，發展能力，靈活運用結構，形成結構化思維，從而促進學生形成合理的認知結構，培育主動建構數學知識的心向，提高自主建構數學知識的能力。數學知識的整體結構教學是指改變由局部到整體，將數學知識列為一個個知識點進行教學，依據數學知識之間的本質聯系和內在結構，以知識理解和存儲結構的特點進行數學知識的結構教學，在數學知識結構內部進行操作，強化通過既定的認知發展階段吸收新的知識的過程，使學生熟悉這些結構，并更好地掌握它們的復雜性，反過來又促進新知識的獲得，如此循環往復直至學習者的認知結構與知識結構取得一致。在此，筆者歸納了以下幾種常見的教學策略：

一、“結構遷移”的教學策略

“結構遷移”是指將數學知識的學習分為“結構”的認識與“結構”的應用兩個階段，這兩個階段不僅體現在不同單元知識的學習。也體現在同一單元知識學習以及同一節課內知識的學習。在“結構”認識階段，要讓學生在學習過程中發現結構的存在，充分感悟和體驗知識之間關聯的結構。在“結構”運用階段，要引導學生靈活運用“結構”主動學習結構類似的相關知識，在結構運用過程中進一步完善對結構的理解和修正。例如，在函數知識模塊中，一次函數的學習是“結構”認識階段，反比例函數與二次函數的學習是“結構”應用階段，在一次函數學學習中，要讓學生在學習中形成函數解析式與函數圖像“數與形”兩個維度之間的相互依存的方法結構（如右上圖），在后繼函數知識的學習中就可運用這一結構主動也進行類似研究活動。以二次函數為例作進一步說明，二次函數教材是按認識二次函數解析式，再認識二次函數圖像編排，而圖像又是按頂點在原點，頂點在y軸上，頂點在x軸上，再按一般二次函數圖像的順序安排，教學中若教師缺乏對各知識點之間關系的關注意識，易造成學生如“盲人摸象”式被動地學習，如果引導學生運用一次函數圖像與解析式相互依存這一結構關系進行學習，學生就能想到二次函數圖像與其解析式相互依存，明確研究二次函數圖像的具體思路：

二、“自上而下”的教學策略

基于基本的簡單技能能被逐步組合為更加復雜的技能的立場，傳統教學將知識進行分割，以從局部入手累積為整體的自下而上的方式進行學習。“自上而下”教學策略是指按照人類認識事物由整體到局部的自然順序開展教學，使知識的獲得與知識的組織與儲存相吻合，促進高層次思維水平的形成。自上而下的教學策略與自下而上的教學策略是相反的，但不應視它們為兩種對立沖突的教學策略，而應當看做是在不同的時期為了不同的目的所運用的互補策略，前者著眼于技能的掌握，而后者適合于高層次思維的形成。“自上而下”教學策略的操作方式：

從整體背景入手到局部知識的結構教學

從整體背景入手到局部知識的結構教學適用于單元知識起始的教學，可在單元之間學習一周前在教室公布單元知識的概念地圖（知識結構圖），讓學生整體認知單元知識背景，并作必要的背景知識準備，下面以旋轉的引入為例：

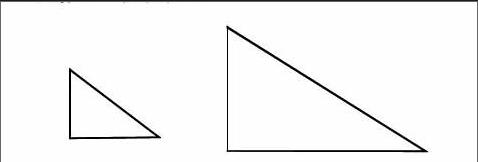
問題1：你能將下列的兩個全等三角形按運動類型分類嗎？

問題2：說說你分類的標準是什么？

問題3：各種運動類型有什么特征？

設計意圖分析：圖形按運動類型分類讓學生對圖形的常見運動有整體的感知，學生已經學習了圖形的平移、軸對稱（即翻折），就更加自然地將旋轉的學習與原有的圖形運動相結合起來，對學習的內容整體感知后能整體把握，充分感悟和體驗知識之間關聯的結構。這樣，學生容易將原有的學習經驗遷移到新的學習知識上來，進而促進學生的認知結構發展。

三、“自下而上”的教學策略

該教學策略是指下位學習的結構教學，下位學習是指學生認知結構中原有的知識在包攝性和概括水平上高于新學習的知識，下位學習比上位學習更容易實現知識的同位與遷移。因此，在教學中先呈現最一般的、包攝性最廣的概念，然后逐漸呈現越來越具體的概念。

例如，在學習了相似圖形的基礎上學習相似三角形的定義時：

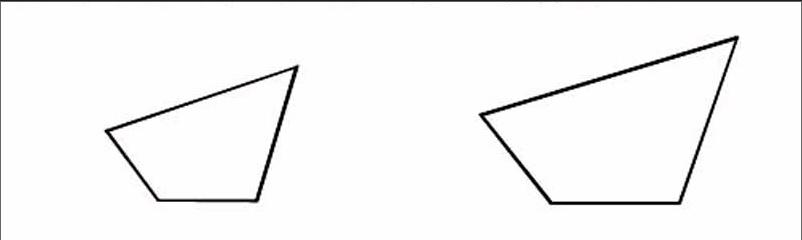
問題1：請結合右圖說說什么是相似圖形？

問題2：在相似多邊形中，最簡單的就是相似三角形，請結合下圖說說什么是相似三角形？

設計意圖分析：學生認知結構中原有的知識相似圖形的概念，在包攝性和概括水平上高于新學習的知識相似三角形的概念，在學習時學生容易實現原有知識向新知識的同位與遷移。因此，教學中先呈現最一般的、包攝性最廣的概念，然后呈現具體的概念。這樣，既有利于相似三角形概念的掌握，也有利于知識結構的發展。

四、“復合結構”的教學策略

“復合結構”是從復雜問題解決中發現技能的結構教學，讓學生首先從復雜的問題入手，借助高級思維活動來學習，通過獨立探索（包括同伴互助和教師幫助）找到或發現所需要的基本技能。

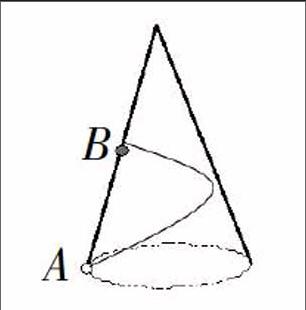
下面以圓錐側面積公式教學作簡要說明：傳統圓錐側面積公式的教學，學生先由教師的簡單講解獲得公式，然后在反復練習中運用公式。我們以從復雜問題入手發現技能的結構教學作如下改進：

問題1：我們已經知道圓柱的側面積公式為（其中r是底面半徑，h是母線長），今天我們探討如何計算圓錐的側面積（提供圓錐模型），這次由你們自己去做，你們可獨立探索，也可互助研究，你們不僅要得到圓錐的側面積公式，還要準確解釋公式是如何推導出來的。

問題2：如何制作一個與它相同的圓錐（出示圓錐模型）。

問題3：若位于A點的小蟲沿圓錐（母線長為6，底面半徑為3）的

側面爬行一周到A點，求爬行路線的長。

設計意圖分析：問題1以類比思想提出研究圓錐側面積計算公式，讓學生從解決復雜問題入手，在解決問題中獲得圓錐的側面積算公式，在公式的獲取中發展了學生高層次思維能力。問題2以逆向思維提出富有現實意義的問題——制作圓錐，讓學生在解決問題過程中發現圓錐側面展開扇形與圓錐底面半徑和母線長的關系。問題三是綜合運用前面獲得的數學知識和解題策略，進一步提高學生的思維水平。通過這樣的學習活動，學生獲得的不只是孤立的認知和對圓錐側面積公式簡單運用的技能，而是把握住了解決問題的核心策略，也就是平面圖形與立體圖形之間的相互轉化以及轉換中數量的不變性，促進學生形成良好的問題解決認知結構。

數學認知結構的發展既關系到學生能否順利完成后續學習，也關系到學生能否牢固掌握和深度理解原有知識。揭示知識的本質和知識間的內在聯系，用知識結構來發展認知結構，用認知結構進一步鞏固知識結構，使數學的學習變得更加輕松、更加美妙。

參考文獻：

[1] 吳亞萍.“新基礎教育”數學教學改革指導綱要[M].桂林：廣西師范大學出版社，2009.

（作者單位：浙江省仙居縣新生中學 317300）