巧用“錯誤”資源，營造高效課堂

曹素燕

[摘 要] 初中階段的學生，仍然懷揣著小學時的童真，對待學習不能全身心地投入，尤其是在課堂上，常常會犯下很多的錯誤. 因此，要想讓學生們在課堂上能夠聚精會神，營造出高效的學習課堂，教師們就應該從學生的本身出發(fā)，去發(fā)現(xiàn)學生的問題，引導學生解決問題，方能在成績上有所突破. 其中，巧用學生們犯下的“錯誤”，將這種“錯誤”當作一種資源，反饋給學生們，將是提升課堂品質的有效選擇.

[關鍵詞] 初中數(shù)學；錯誤資源；高效課堂

在學生階段，伴隨著自己成長的不僅僅是周圍的同學，“錯誤”也在伴隨著我們的成長. 作為學生，出現(xiàn)各種各樣的“錯誤”是十分正常的，也只有學生犯錯誤了，教師才能發(fā)現(xiàn)學生的不足. 但是，在實際的教學中，筆者發(fā)現(xiàn)許多教師不知道如何對待學生們的錯誤. 而筆者認為，教師在遵循“以人為本”教學理念的同時，更應該關注每一位學生的實際情況，讓學生正視自己的“錯誤”，在改錯中反思和總結、領悟方法，拓展自己的思維. 也只有教師巧用學生們的這種“錯誤”資源，使學生正視了自己的“錯誤”，才能打造一番高效課堂的景象.

巧用“錯誤”資源，激發(fā)學習興趣

初中生學習中最能夠活躍課堂的因素就是興趣. 因此，在教學的過程中，筆者尊重且理解那些出錯的學生，并用學生自己犯下的錯誤作為教學資源去激發(fā)學生的學習興趣和學習熱情，讓學生們在錯誤中積極思考與總結，不斷地完善自己.

例如，筆者在課上給學生們出了這樣的一道題：某種電腦病毒傳播得非常快，如果有一臺電腦被感染，那么經(jīng)過兩輪感染后就會有81臺電腦被感染. 請學生們用學過的知識分析每輪感染中平均一臺電腦會感染幾臺電腦？倘若病毒得不到有效的控制，3輪感染后，被感染的電腦會不會超過700臺？

大部分的學生在做此題時，首先會設在每輪感染中平均一臺電腦感染x臺電腦，列方程x2=81，然后解出方程. 這時筆者會針對學生的錯誤解答，讓學生們自己去分析解答是否正確，并自由討論. 當討論結束后，有學生說“第一輪感染后應該有（x+1）臺電腦被感染病毒”時，筆者沒有立即評判對錯. 在這位學生提出自己的想法時，其余的學生也會自然而然地去活躍自己的思維，去考慮這位學生的敘述. 通過學生間的討論，他們發(fā)現(xiàn)了在第二輪感染之后，新感染的電腦就會有x（x+1）臺，同時加上第一輪感染的（x+1）臺，就會得出（x+1）2=81，然后解出正確答案. 就這樣通過學生們犯下的錯誤，再一次用錯誤去引導學生思考，激發(fā)他們的學習興趣和探究欲望.

興趣是學生們求知的內(nèi)動力. 筆者在給學生出題目時，讓學生們先思考，先自主解答，之后從學生們身上發(fā)現(xiàn)普遍存在的錯誤，利用這樣的錯誤資源，引發(fā)學生們學習的興趣，有了興趣，學生會主動地探究，有利于高效課堂的形成.

巧用“錯誤”資源，激發(fā)探究欲望

如果說解題是數(shù)學的第一陣地，那么“錯誤”就是數(shù)學的第二陣地. 學生在解題過程中必然會出現(xiàn)錯題，而這種錯題恰恰是一筆巨大的資源，這種資源也只有學生自己才能享受到. 但是往往大多數(shù)的學生忽視了這種資源，這就要求教師們要在今后的教學過程中不斷地引導，而不是當學生做錯時，直接告訴學生正確答案，這樣反而會限制學生主動性和創(chuàng)造性思維的發(fā)展，只會得到事倍功半的效果. 教師如果對學生們的這些錯誤進行巧妙利用，將會使學生自主發(fā)現(xiàn)錯誤，從而提高學習的積極性，激發(fā)學生們自主探究的學習欲望，日積月累，將培養(yǎng)學生們的探究能力，能得到事半功倍的效果！

例如：在學習“圓”這一節(jié)時，筆者給學生設計了這樣的一道題：一個鈍角三角形，用圓去完全覆蓋，怎么樣能使得圓最小？

有學生回答最小的圓就是這個鈍角三角形的外接圓，而大部分的學生都同意這位學生的說法. 這時候，筆者意識到學生們這樣的錯誤極具代表性，于是為了解決這個問題，筆者反問學生：“難道外接圓就是覆蓋住這個鈍角三角形的最小圓了嗎？”面對問題，學生會對自己剛才的想法產(chǎn)生疑惑. 于是，筆者再讓學生自己動手畫出這樣的圓，看看最小的圓是什么. 然后讓學生們互相討論，總結組內(nèi)每位學生的觀點，并進行反思. 學生們從而否決了自己原先的觀點，用假設的方法得出了鈍角三角形的最小覆蓋圓是以其最長邊為直徑的圓. 于是全班同學恍然大悟，通過對自己觀點的再次研究，重新獲得了解題的信心，增強了探究的欲望.

以往的教學中，當學生犯錯誤時，教師僅僅是直接指出學生的錯誤. 而在新課改的標準下，教師們應該引導學生合理地面對自己的錯題. 教師有效利用學生的錯題，因勢利導，使得學生發(fā)現(xiàn)自己的錯誤，在初步感受數(shù)學思想的同時，學生的思維能力與探究能力得到了極大的提升. 由此可見，巧用“錯題”資源，將是打造高效課堂的一把金鑰匙！

巧用“錯誤”資源，培養(yǎng)發(fā)現(xiàn)意識

數(shù)學是一門探究性學科，這種探究性要求學生們要具有發(fā)現(xiàn)的意識. 學生們要知道，數(shù)學的方法、知識以及思想不是單純地依賴教師的傳授，更多的是自己在學習生活中，不斷地積累，不斷地發(fā)現(xiàn)，用自己的發(fā)現(xiàn)意識，將別人的東西轉化成自己的東西. 在實際的教學過程中，筆者根據(jù)每位學生的不同，從每位學生的“錯誤”入手，挖掘錯誤中潛在的智力因素，根據(jù)學生們的錯誤提出具有啟發(fā)性的問題，引導學生在改錯的過程中，培養(yǎng)自己的發(fā)現(xiàn)意識.

例如，在教學“圓錐的側面積與全面積”這一節(jié)時，筆者給學生設計了這樣的一道題：圓錐的底面半徑為1，母線長為3，一只螞蟻要從底面圓周上一點B出發(fā)，沿圓錐側面爬到過母線AB的軸截面上另一母線AC的中點D上，求螞蟻爬行的最短路程是多少？

在給出這道題時，首先筆者讓學生自己獨立尋找螞蟻從B到D爬行的最短路線，學生們思考一番后，認為連接B，D兩點即可. 從教師的角度出發(fā)，筆者想學生們肯定把平面內(nèi)“兩點之間線段最短”與立體圖形中的定義混淆了，于是筆者再次追問學生們螞蟻真的能從大家規(guī)定的路線爬行到D點嗎？讓學生們再次討論，筆者告訴學生要仔細讀題，既然題目已經(jīng)規(guī)定螞蟻只能沿圓錐側面爬行到D點，那么螞蟻就不能直接從圓錐的內(nèi)部通過. 當給出這樣的點撥，學生們恍然大悟，將圓錐展開成扇形，方能運用“兩點之間線段最短”的定義，正確地解出答案. 本題中，筆者就是將學生的“錯誤”當作一種資源，引導學生們?nèi)ヌ骄浚囵B(yǎng)學生的發(fā)現(xiàn)意識.

通過本題，相信大家可以看出，學生們很天真地將平面幾何的知識與立體幾何的知識混為一談，導致了錯誤的發(fā)生，但是通過筆者在學生思維活動過程中的引導，學生們再次拾起錯題，通過探討發(fā)現(xiàn)了錯誤的原因，然后不斷地總結與反思，大大加強了學生們的探究意識. 由此可見，巧用“錯誤”資源，讓學生對所學的知識有了更深的理解，同時也無意間培養(yǎng)了學生的發(fā)現(xiàn)意識.

巧用“錯誤”資源，開展創(chuàng)新思維

學生在解題的過程中，常常因為沒有思路而無從下手，導致解題失敗. 學生們遇到這樣的問題往往是因為自身沒有養(yǎng)成良好的思維習慣，再加上沒有過多數(shù)學思想的支撐，在解題中會遇到瓶頸. 因此，教師在教學的過程中，如果有學生遇到問題，教師就需要適時給予學生點撥，幫助學生們打開思路，并且不斷地鼓勵. 日積月累，學生們就會突破思維障礙，達到創(chuàng)新的新境界！

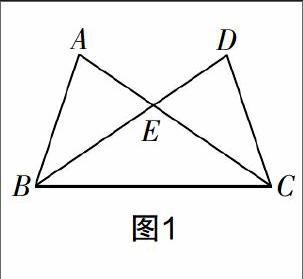
例如，在教學“等腰三角形的性質和判定”這一節(jié)時，筆者給學生設計了這樣的一道題：如圖1所示，有如下四個條件：①AB=DC；②∠ABE=∠DCE；③AE=DE；④∠A=∠D. 任取其中兩個作為條件，不能得到△BEC是等腰三角形的是（ ）

A. ①與② B. ②與③

C. ①與④ D. ①與③

此題的前三個選項學生們都能準確地證明△BEC是等腰三角形，而第四個選項因為條件的原因，學生們無法證明△BEC是等腰三角形，因此學生覺得第四個選項不能證明△BEC是等腰三角形. 但是在學生們都不說話的時候，有位學生說第四個選項也能證明，就是分別過A，D兩點作垂線，先根據(jù)“AAS”，再根據(jù)“HL”方能證明△BEC是等腰三角形. 聽了這位學生的思路，筆者不禁為他的創(chuàng)新思維帶來的精彩演講所折服，看來這道題還需重新編寫. 同時，也正因為這位學生的創(chuàng)新思路，讓學生在不斷質疑、反思的道路上越走越遠，使得創(chuàng)新的思維越用越活.

可見，創(chuàng)新思維意識的培養(yǎng)也是十分重要的. 教師們要讓學生大膽地構思，大膽地創(chuàng)新，不管對與錯，學生們都會在創(chuàng)新中收獲不同的感悟，長期訓練，巧用“錯題”，將幫助學生達到一個新的學習高度，營造高效的課堂.

總之，教師要時刻謹記新課程標準下學生的主體地位，打造以學生為主體的課堂. 師生間不斷地交流，將學生的“錯誤”資源轉化成一筆巨大的財富，好好利用，培養(yǎng)學生的思維能力，養(yǎng)成良好的思維習慣. “錯誤”資源不僅會幫助學生反思自己，獲得成長，也是打造高效課堂的有效方法.