小學數學作業錯例分析與資源化利用摭淡

何瓊瑛

學生作業中的錯例是普遍存在的，仔細分析錯例產生的原因卻發現其中存在差異。從實踐中我們發現，很多學生的錯例是我們教師始料未及的，有些想法甚至很“天真”。因此，教師遇到作業中的錯誤，不能簡單地概括為“粗心”“沒看清題目”等，而要與學生溝通，架設讓學生走出錯誤思維的階梯。

一、錯例歸類整理及成因分析

錯例分析應基于學生的基礎與現狀、學習心理和非智力因素三方面展開，鏈接教師的課堂教學行為和教材編排合理性。錯例分析也應從根本上尋找錯例產生的緣由，挖掘錯例中蘊涵的教學價值，為教師教學提供建議，以減少學生錯例的發生概率。我們在實踐中總結、提煉了八大錯例及相應的教學策略（案例選自人教版教材及配套練習）。

1.知識性錯誤——對照矯正

在六年級下學期學習完“正反比例的意義”后，學生對于正反比例的判斷存在很大的困難，尤其若題目涉及圓形的周長、面積和體積則更難于區分。

如：圓的周長和它的直徑（ ）；圓的面積和它的半徑（）。

六年級備課組通過學生錯例分析后一致認為：學生存在此類知識性錯誤的原因是學生初涉正反比例，對于抽象的無數據支撐的圖形類判斷缺乏有效的解答策略。提出增加一課時專項訓練、對照矯正的教學建議，設計以下主要教學環節：

（1）討論：圓的周長和它的直徑成（ ）比例，說明理由。

（2）引導學生小結方法，可以利用假設法，列表解答，觀察兩個對應量的商或積是否一定。

（3）討論：圓的（ ）和它的（ ），（ ）比例，說明理由。

（4）引導歸納有關圓的正反比例關系。

（5）獨立研究：__（圖形）的__和__，（ ）比例。

2.方法性錯誤——重點矯正

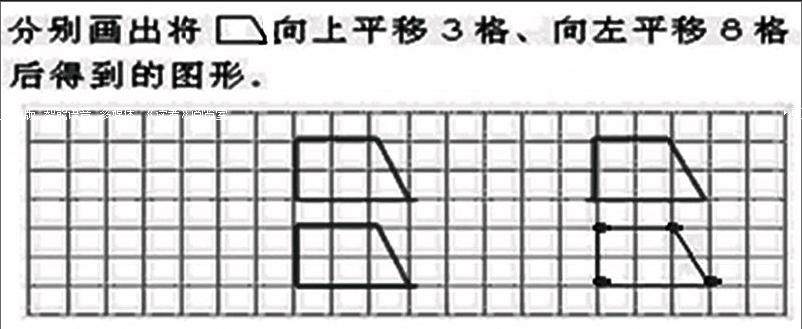
二年級下冊教科書43頁有這么一道練習題。

一教師統計了授課班級，并結合年級其他班的答題情況，反映有大部分學生無法正確理解中“分別”一詞。認為題目的要求就是“畫出將圖形先向上平移3格，再向左平移8格后得到的圖形”。該教師認為：學生是混淆了“先A再B”與“分別A，B”兩種題型，產生混淆的原因是學生語言理解能力發展不完善。提出了以下矯正建議：

（1）在課堂教學設計中增加兩種題型的對比，注重學生語言表達能力的訓練。

（2）教學時設計提問：什么是“分別”？把“分別”一詞去掉該怎么說？

（3）類似“分別”、“各”等字詞，往往“隱蔽”在語句中，要善于發現、更要善于去掉。

3.習慣性錯誤——變式矯正

一年級上冊“10以內加減法”單元，配套《課堂作業本》第36頁第4題。

一教師統計發現本題錯誤率高達83%，認為學生受“熟題”的干擾而發生“習慣性錯誤”。學生在學習中，通過聽老師講、做練習等形式，積累了一定量的“經驗題”，學生一旦遇到類似問題，便不假思索，以偏概全地分析問題，按原來形成的思路解答和得出答案。該教師提出以下教學建議：

（1）變式矯正，防止負遷移

根據學生的認知水平，選擇具有針對性的題目，組織學生進行觀察與思考。

-2 -3 -1 +6

8→口→口→口→口

8-2=口-3=口+1=口+6=口

（2）巧用比喻，杜絕負遷移

師生共同為題目起名字，把第1題命名為“算式接龍”，把第2題命名為“算式天平”。

4.普遍性錯誤——集中矯正

一年級第2冊配套《課堂作業本》第18頁上有一道題：

畫一畫，數一數。墻上缺了（）塊磚。

圖形本來是很直觀的，但利用它的直觀特點解題時，要發現其中蘊含的規律就不是簡單能畫出來的。教師提出教學建議：

（1）解答方法：截取的長度相等，每層磚頭數目均為7塊；每層缺少的磚塊=7一已知的磚塊；計算得出每層缺少的磚頭數，總共缺少的塊數。

（2）根據計算得數畫出直觀圖，重點研究畫的規律。

（3）幾何直觀，通過畫圖的方式來理解；邏輯思考，通過數形結合的方式來理解。

5.結構性錯誤——完善認知

五年級學生在學習方程單元后，遇到諸如未知數是減數、除數時，利用等式的性質解答就比較麻煩。教科書為了避免這個“麻煩”，從教材上刪除了此類方程，但在方程的實際應用中，是無法避免的，如用方程解答：

一堆煤炭0.8噸，用了兩天后，還剩下0.5噸。平均每天用多少噸？（0.8-2x=0.5）

學生對于兩種解法有各自的想法：

解法一：0.8-2x=0.5

0.8-2x+0.8=0.5+0.8（兩邊同時加上0.8，就把左邊的0.8去掉了）

2x=1.3

2x÷2=1.3÷2

x=0.65

解法二：0.8-2x=0.5

2x=0.8-0.5（一共0.8噸，最后剩下0.5噸，所以兩天是用0.3噸）

2x=0.3

2x÷2=0.3÷2

x=0.15

教師在診斷分析學生的想法后，提出以下觀點：

（1）如果避免未知數是減數、除數的方程，對于學生的認知結構是不完整的。

（2）學生的解法二給教學這類方程提供了思路，四則混合運算順序的教學可以與情境結合，方程何嘗不可，先結合情境研究解法，再總結解法、舉一反三。

（3）完善學生的認知結構，才更有利于學生掌握知識之間的邏輯關系。

6.意料錯誤——設計矯正

六年級下冊配套《作業本》第42頁有這樣一題：為慶祝元旦，三（1）班同學做小紅旗（如圖）。現在有一張長1.4米，寬0.9米的長方形卡紙，最多可以做這樣的小紅旗多少面？

學生可能有兩種解答方法：

方法一：1.4米=14分米，0.9米=9分米

（14×9）÷（2×2÷2）=63（面）

方法：1.4米=14分米，0.9米=9分米

14÷2=7（面）9÷2=4（面）7×4×2=56（面）

教師在訪談后發現：學生已經較好地掌握了圖形分割問題的解答方法，能說清楚其中的緣由，能將等腰直角三角形轉化成正方形再解答。但，正確答案是60面（如下圖），此類錯例的產生是教師預料之中的，標準答案的解法需要利用“勾股定理”計算，而六年級的學生根本沒有這個基礎，本題出題不當。

重新定位本題的功能后，六年級備課組提出以下教學建議：

（1）本題改為思維拓展，不要求人人掌握，標準答案可供學生參考。

（2）組織學生討論兩種方法，各自稱述理由，重點掌握。

（3）提示換角度思考：四個等腰直角三角形也能拼成正方形，了解畫法。

（4）畫一畫、量一量、算一算。

二、錯例資源化利用

在研究過程中，我們感到這些錯例資源的重要作用與對現實教學的重大指導意義，如果只是將其收集、整理，那么對錯例的利用是不充分的。如何將這些分門別類，具有年級特點的錯例資源化呢？帶著這樣的思考，我們進行了探索：

1.錯例資源的傳承制

教師記載的錯例絕不能用完就扔，可成為檔案資料。新學年任教教師傳承上屆教師記錄《錯例記載本》，作為二度備課的主要參考資料，在備課過程中繼承、分析記載的錯例。這樣的傳承方式首先能使教師的二度備課更有方向性。學生在哪些地方容易出錯，學生對這類問題的認識起點在哪里……這些思考都能從上屆教師的記載與分析中得到一定的科學回答，同時也避免了重復、低效勞動，讓教師有更多的精力繼續深入地看待錯例，進行補充，使得我們的錯例資源更加完整。

2.錯例資源的網絡化

隨著網絡的不斷進步，網絡資源共享錯例成為了可能。教研組可將教師撰寫的錯例分析進行整理，統一上傳學校網站FTP和教研組文件，進行網絡的共享與合作，讓錯例資源在分享中被反思、被質疑、被充實，從而使之更合理。

3.練習題庫建設

我們建立了人教版全十二冊練習題庫。題庫的建設基于對錯例研究的成果，基于教師對學生的起點進行科學定位，基于對教學內容重難點的有效把握，將練習有層次、有實效地排布。教師執教時可以自主地選擇適合本班學生的題目，進行針對性的練習；學生、家長也可以利用班級QQ群資源共享，有針對性地進預習、復習。