一道中考題的解法分析與教學思考

廈門市海滄中學(361028) 藍文英

一道中考題的解法分析與教學思考

廈門市海滄中學(361028) 藍文英

1 試題呈現

(廈門卷第 25題)如圖,在平面直角坐標系xOy中,已知 點A(1,m+1),B(a,m+ 1),C(3,m+3),D(1,m+a),m＞0,1＜a＜3,點P(n?m,n)是四邊形ABCD內的一點,且△PAD與△PBC的面積相等,求n?m的值．

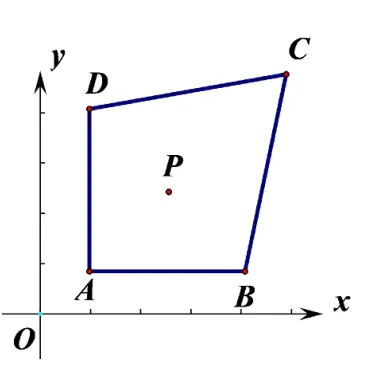
圖1

2 優點解讀

2.1 能力立意,數形結合

本題立足能力,涵蓋知識點多,綜合性強,具有較高的思維含量,考察學生的觀察能力和基本經驗與技能.以圖形為載體,要求學生有較強的數感,能夠借助圖形,透過現象看本質,利用幾何直觀進行知識遷移.既檢測學生的推理判斷能力,又考查數學的數形結合與轉化思想,試題具有很深的立意與延展性功能.

2.2 圖形簡潔,凸顯思維

本題以四邊形為背景,文字簡約,圖形簡潔,但卻蘊含著數學的核心思維.能否通過四邊形四個頂點的坐標建立四邊形邊與邊、邊與坐標軸以及點P與四邊形的頂點、邊、對角線的聯系,能否借助面積相等構造方程模型,能否通過幾何直觀、空間想象、圖形變換聯想箏形ABCD是軸對稱圖形而AC恰巧是對稱軸,能否通過輔助線的添加探索點P的位置,能否透過驗證發現點P在直線AC上,建立函數模型.這無疑對考生有較高的思維要求以及借助已有知識經驗解決問題的能力.

2.3 形式創新,解法多樣

在平面直角坐標系中研究圖形變換是本題的一大特色,整個圖形蘊藏著大量的數量關系,為學生解決問題提供了豐富的思維源泉.借助坐標系無疑打通了幾何與代數的橋梁,由形推數,由數及形,相得益彰.從位置關系、圖形關系的探究到數量關系的探究,從而衍生的解決問題的方法不僅多樣而且新穎,精巧.一題多解、一法多用,豐富精彩的解法最終以不變應萬變,充分發展學生的思維能力.

3 試題多解

結合圖形分析題目條件,不難發現本題的突破口是應用數形結合思想及方程、函數思想,下面從“幾何直觀”這一核心素養建立不同的形與數的關系以及利用數形關系深入探析多種解法.

3.1 構建模型意識,立足常規解法

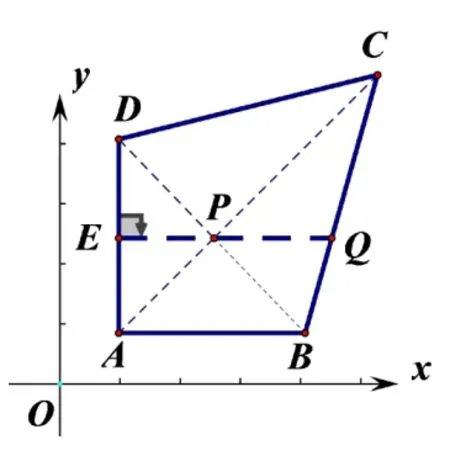
圖2

解法1: 如圖 2,過點P作PQ//AB交BC于點Q,延長QP交AD于點E,則依題意得PE⊥AD,∵A(1,m+ 1)、B(a,m+1)、C(3,m+3),D(1,m+a),P(n?m,m),m＞0,1＜a＜3,∴AB//x軸,AD//y軸,E(1,n),AB=AD=a?1,AB⊥AD,∴PE=n?m?1,∴

又∵S△PAD=S△PBC,∴①式和②式相等,比較分子即可.又∵1＜a＜3∴a?1/=0,∴?(n?m?3)=n?m?1.∴n?m=2.本法屬于常規解法,借助三角形面積相等,構建方程以及函數模型,學生利用已有知識經驗,立足通性通法,把未知量轉化為已知量,充分考察學生的識圖能力和數學的轉化思想.

3.2 借助數學結合,搭數形數橋梁

妙法簡析: 如圖3,過點C作CF⊥AB交AB的延長線于點F,過點C作CE⊥AD交AD的延長線于點E,則CE=xC?xD=3?1=2,CF=yC?y?B=(m+3)?(m+1)=2,∴CE=CF,同理ED=BF=3?a,∴Rt△CDE～=Rt△CFB(SAS),從而CB=CD.又∵AB//x軸,AD//y軸,∴AB⊥AD,又∵A(1,m+1)B(a,m+1)、D(1,m+a),∴AB=AD=a?1.因此,四邊形ABCD是軸對稱圖形,AC是對稱軸,且AC是BD的垂直平分線.不難發現,四邊形ABCD也是箏形ABCD.接下來,確定點P的位置,通過挖掘點P與頂點A、B、C、D的關聯(即點坐標的特征),挖掘點P與四邊形ABCD邊的關聯(即邊的特征),挖掘點P與四邊形對角線AC、BD的關聯(即形的特征)可衍生三種巧妙解法.

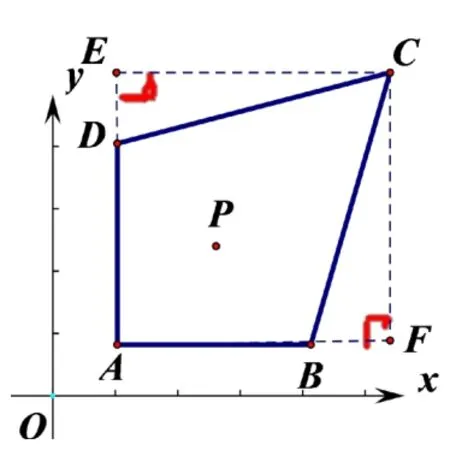
圖3

解法2:如圖4,∵A(1,m+ 1),C(3,m+3),P(n?m,m),觀察發現這三點的坐標有個共同特點:縱坐標=橫坐標+m,這就說明點P在直線AC上,并且直線AC的解析式為y=x+m(或利用待定系數法驗證求得).又∵1＜a＜3∴a?1/=0,∴n?m?1=1,∴n?m=2.

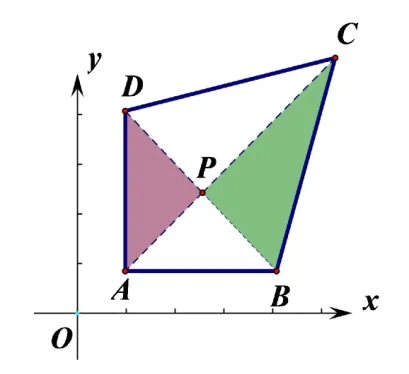
圖4

解法3:如圖5,過點P作PM⊥DA,PN⊥AB,垂足分別為點M和點N.∵P(n?m,m),∴點P到邊AD的距離PM=?m?1,點P到邊AB的距離PN=n?m?1,∴PM=PN,∴點P在的角∠DAB平分線上,即點P在對稱軸AC上.由對稱性進一步得到S△PAD=S△PAB,又由已知條件S△PAD=S△PBC,∴S△PAD=S△PAB=S△PBC=S△PDC,∴點P在AC的中點上.根據中點坐標公式:

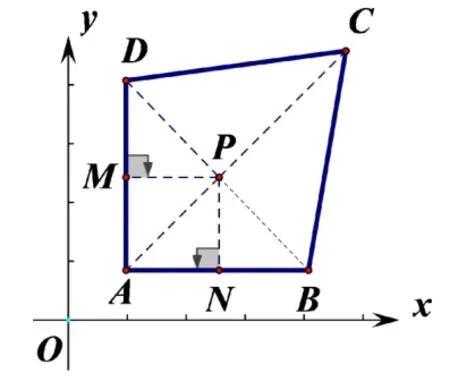
圖5

解法4:如圖5,觀察點P與對角線的關聯,點P是否在AC、BD上,進而轉化為判定點P是否在直線上的函數問題.設直線AC的解析式為y=kx+b(k/=0),∵A(1,m+1)、C(3,m+3),根據待定系數法,求得直線AC的解析式為y=x+m,又∵P(n?m,m),顯然點P的坐標滿足直線AC的解析式為y=x+m,因此判定點P必然在AC上.故而,過點P作PM⊥DA,PN⊥AB,垂足分別為點M和點N.∵P(n?m,m),∴點P到邊AD的距離PM=n?m?1,點P到邊AB的距離PN=n?m?1,∴PM=PN=n?m?1,又∵AB=AD,同底等高所以有S△PAD=S△PAB,又由已知條件即

解法5:觀察點P與對角線的關聯,點P是否在AC、BD上,進而轉化為判定點P是否在直線上的函數問題.設直線AC的解析式為y=kx+b(k/=0),∵A(1,m+1)、C(3,m+3),根據待定系數法,求得直線AC的解析式為y=x+m,又∵P(n?m,m),顯然點P的坐標滿足直線AC的解析式為y=x+m,因此判定點P必然在AC上.由于一三象限的角平分線為直線y=x,因為m＞0,將直線y=x向上平移m個單位就得到直線AC∶y=x+m,顯然兩條直線平行,因此AC平分∠DAB,無需作輔助線PM、PN.根據軸對稱的性質和已知條件S△PAD=S△PBC,

解法2至5屬于個性解法中的妙解,觀察分析四邊形ABCD頂點坐標的特點,從“點坐標的特征”探究出四邊形“邊的特征”,進而獲得整個四邊形“形的特征”,層層遞進,思維螺旋上升.正如著名數學家徐利治教授所言:“幾何直觀是借助見到或者想到的幾何圖形的形象關系產生對數量關系的直覺感知.”即借助幾何直觀:“用坐標去還原圖形,搭建形和數的橋梁”.以上巧解要求學生擁有較強的數感和空間觀念、直觀想象以及扎實的數學基本知識和基本經驗,不同的切入點體現不同的思維層次,也充分體現命題者借助幾何直觀利用圖形描述、理解和解決數學問題的考察意圖.

4 教學思考

4.1 滲透幾何直觀,提高數學素養

著名數學家華羅庚是這樣描述數和形的關系:“數形本是相倚依,焉能分作兩邊飛;數缺形時少直觀,形少數時難入微;數形結合百般好,隔離分家萬事休”,真可謂一語中的.的確,解題的過程不僅是演繹推理的過程,更是發現和創造的過程,理性的邏輯分析固然重要,但那靈光一閃般的數感或直覺更加難能可貴.數感扎根于幾何直觀、基本經驗、基本思想.一道題最容易想到什么,結合圖形獲得猜想,靠直覺或數感“識骨尋蹤”,從而找到解決問題的突破口.在直觀想象和空間觀念的推動下,經歷觀察、猜想、探究、驗證,思維呈梯度上升,直擊問題核心.比如本題就是看到四邊形ABCD的形狀立馬聯想到邊AB=AD、CD=CB,進而驗證發現四邊形ABCD果然是軸對稱圖形,點P的位置確定則呼之欲出.因此,“直觀想象后的理性分析”顯得尤為重要,是直達學生最近發展區的最短路徑,所以在實際教學中,教師應有意識的滲透幾何直觀,創造數學活動讓學生個體親身經歷,在創造體會中積累數學經驗,提高幾何素養.

4.2 突破思維僵局,觸及幾何本質

盲目的“刷題”無疑會阻礙學生思維的發展,只有建立在多角度、多方位、多元化思維的基礎上的“觸類旁通式”解題才能激發學生濃厚的學習興趣,并促進思維更深層次發展.一題多解、一題多變、一法多用正是幾何題的魅力.無論是自然解法還是個性解法,都立足于扎實的幾何基本知識與識圖能力.本題就是一個很好的詮釋,比如觀察四邊形ABCD頂點的坐標的特點,得到AB//x軸,AD//y軸并且AB=AD;而觀察C、B、D三點的坐標,通過不規則四邊形補形為正方形或作垂直構造Rt△、證全等得到CD=CB,進而獲得“四邊形邊的特征”,這便是解這道題的基石.在直角坐標系中研究圖形的數量特征,用坐標還原圖形,如果解法1是常規解法,那么解法2至5則開始打破常規思維,不僅思考問題的角度多元化,思維更是得到發散與延展.因此,教師在平時的解題教學中,不僅要引導學生開闊思路,強化幾何直觀意識,積累基本經驗和技能,拔高思維層次,實現解題最優化.

5 結語

幾何直觀是《義務教育數學課程標準》(2011年版)提出的一個核心概念,它是借助圖形和空間觀念描述與分析問題的輔助手段,可以使復雜的數學問題簡單化,是代表圖形與幾何的核心素養.與知識技能的學習不同,它是通過學生在不斷解決問題的過程中慢慢“感悟與滋養”而來.因此,教師在實際教學中,需要為學生提供一片沃土讓其生根、發芽.

[1]義務教育數學課程標準修訂組.義烏教育數學課程標準(2011年版)解讀[M].北京:北京師范大學出版社,2012

[2]章建躍,薛彬.義務教育教科書.數學(八年級下冊)[M].人民教育出版社,2015

[3]王忠剛,王志進.一題多法的產生力求自然[J].中學數學教學參考:中旬,2016(3):40-41

[4]黃祥勇,榮彬.基于“直觀想像”核心素養的教學啟示[J].中學數學教學參考:中旬,2016(9):55-58