談談解題后的再反思

廣州市從化區鰲頭中學(510940) 薛喜雙

談談解題后的再反思

廣州市從化區鰲頭中學(510940) 薛喜雙

數學教學是以解題為中心展開的,要培養和提高學生的解題能力,除了做好審清題意、制定解題計劃、實施解題方案等工作之外,解題后的再反思也是一個不可缺少的重要環節.

所謂解題后的再反思是指在解決了數學問題后,通過從問題特征、解題思路、解題途徑、解題過程、題目結論等方面進行反思以進一步摸清數學解題所經歷的前因后果的思維過程.如果學生在每一次解題以后都能對自己的解題思路、過程、策略總結歸納作自我評價,探討成功的經驗和失敗的教訓,對解題過程中反映的數學思想、方法進行總結、概括,就一定能達到提高解題能力和優化思維品質的目的.

下面是筆者在教學過程中引導學生進行反思的幾點具體做法.

一、反思錯誤原因,及時反饋糾正

學生在學習基礎知識時,不求甚解,滿足于一知半解,加之做作業時粗心大意,考慮問題不全面,這是造成錯誤的主要原因;比如,在求幾何線段的最大最小值問題中,在沒有理解點的運動本質的前提下,隨意利用三角形邊長和差定理,就比較容易出錯.如下例:

例一如圖1,Rt△ACB中,∠ACB=90°,AC= 8,BC=6,E是斜邊上的一個動點,BD⊥BC于B,F為BD上的一個動點,當AE=BF時,求CE+CF的最小值.

圖1

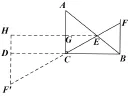
圖2

分析與解:如圖2,作點F′與F關于點C對稱,連接EF′,顯然有CE+CF′≥EF′,所以當C、E、F′共線時,CE+CF′=EF′最小,此時,BC=CD=6,AB=10,設AE=BF=x,

通過上述的再反思,學生不僅發現了自己思維過程中的不足之處,從而完善了解題過程,同時也提高了他們發現問題的能力,訓練了思維的嚴密性和批判性,有利于養成嚴謹細致的學習習慣.

二、反思題目特征,理清條件與結論的關系

解完一道題后,通過反思題目特征,研究條件與結論之間的必要性或充分性,或借變式探究更一般性的結論,可以加深對題目本質的領悟,從而獲得一系列的思維結果,有助于培養學生思維的深刻性和廣闊性.

例二如圖3,梯形ABCD中,AB//CD,∠ABC=90°,AB=BC=5,DE=4,∠EAD=45°.求△AED的面積.

圖3

圖4

解:構造正方形ABCF,將△AFD繞點A旋轉90°到△ABG的位置,如圖4,易證G、B、C三點共線,且△AEG～=△AED,EG=ED=4,所以,△AED的面積等于△AEG的面積,等于

事實上,這是一道錯題,設DF=x,由DE=BE+DF知,BE=4?x,EC=x+1,DC=5?x,在Rt△DCE中,(5?x)2+(x+1)2=42,化簡,得x2?4x+5=0,顯然Δ＜0由知,題目中所給數據矛盾,題目出錯.

以上類似的錯誤,在教學過程中,其實很常見,而出現這樣錯漏的原因也很復雜,有客觀、主觀原因,或由時間環境導致,更有教學水平高低因素等.如下例:

例三已知△ABC中,A(3,6)、B(?2,1)、C(1,4),求BC邊中線AD的長及∠A平分線AE的長.

再反思:∵kAB=kAC,∴A、B、C三點共線,它們不能構成三角形.誤解中用代數計算的方法掩蓋了三角形不存在的事實,這也是一個錯題.

三、反思解題方法,尋求最佳方案

解題是學生往往滿足于做出解答,而對自己解題方法的優劣卻不加分析,作業中經常出現解題方法單一,思路狹窄,過程繁瑣,缺乏靈活性的情況.因此教師必須引導學生評價自己的解題方法,努力尋找解決問題的最佳方案.

例四已知拋物線C1∶y=2x2?3x?5與拋物線C2∶y=?x2?x+4交于點A、B,求直線AB的解析式.

解:先分別求出A、B點坐標,消去y,得

以上求解直線方程的過程,計算顯然比較繁瑣;有沒有較好的方法呢?我們作進一步的研究,下面的方法顯然能夠避免繁瑣的計算,通過巧妙設置經過交點A、B的“函數圖像系”,即可輕松求得正確的結果.設所求直線AB的解析式為:

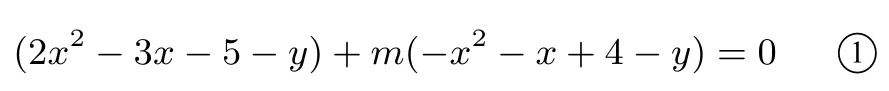
當2?m=0時,m=2,①式變為直線AB的解析式:

四、反思問題本質,及時進行推廣

解決問題以后再重新剖析其實質,可使學生比較容易地抓住問題的實質,在解決了一個或幾個問題以后,啟發學生進行聯想、類比,揭示問題的一般規律.

例五.如圖5,已知AD是△ABC的高,∠BAC=45°,BD=2,DC=3.求AD的長.

略解與反思:如圖6,原題是將△ADB、△ADC分別沿直線AB、AC翻折到△ABE、△AGC的位置,得到正方形AEFG,最后利用勾股定理可求得AD=6.

再探索的問題是,如果將∠BAC=45°改為60°或75°或120°或150°呢?能否改為更一般的角度呢?其實答案是肯定的.

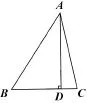
圖5

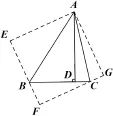
圖6

事實上,按原題輔助線的作法,解決變更角度后的問題,也是可行的,只不過要用到余弦定理等超綱內容,如果換一個思路探索,我們可以得出更一般化的結論.設∠BAC=α, 0°＜α＜90°.

圖7

以上從四個方面,簡單介紹了解題后再反思的點滴做法.這種再反思顯然能提高課堂教學效果,發展學生數學能力,我們在教學中要堅持讓學生獨立思考,培養學生在解題后對解題思維過程進行再反思的學習習慣.