追根溯源 生成概念
——HPM視角下的初中函數(shù)概念的教學

廣州市二中蘇元實驗學校(510000) 王碧瑩

追根溯源 生成概念
——HPM視角下的初中函數(shù)概念的教學

廣州市二中蘇元實驗學校(510000) 王碧瑩

函數(shù)是描述千變?nèi)f化的現(xiàn)實世界的數(shù)量關系中最基本、最重要的數(shù)學模型,函數(shù)概念是中學數(shù)學的中心概念之一．但是,由于函數(shù)是人類對客觀事物的認識由相對靜態(tài)上升到動態(tài)的飛躍,比較抽象,而八年級學生的認知水平還處于具體運算和形式運算的過渡發(fā)展階段,因此,函數(shù)概念是初中學生學習過程中最困難的概念之一,初中函數(shù)概念的教學是一線老師關注的熱點．

HPM,即History and Pedagogy of Mathematics,是數(shù)學史與數(shù)學教育的簡稱．數(shù)學史融入數(shù)學教育的研究是HPM領域的重要方向之一,是為滿足提高數(shù)學效率而運用數(shù)學知識的一種教學理念[1]．最近,筆者觀摩了林俊偉老師執(zhí)教的人教版《數(shù)學》八年級下冊“函數(shù)與變量”(第1課時)[2],引發(fā)筆者對初中數(shù)學概念教學的進一步思考,與同行交流．

1 活動設計

1.1 聯(lián)系實際,問題引入

問題1.票房收入問題:每張電影票的售價為50元．(1)若一場售出150張電影票,則該場的票房收入是____元;

(2)若一場售出205張電影票,則該場的票房收入是____元;

(3)若一場售出x張電影票,則該場的票房收入y元,則y=___.

思考:

(1)票房收入隨售出的電影票變化而變化,即y隨___的變化而變化;

(2)當售出票數(shù)x取定一個確定的值時,對應的票房收入y的取值是否唯一確定?

(例如,當x=150時,y的取值是唯一、還是有多個值?)答:_______．

問題2.路程問題:汽車以60km/h的速度勻速行駛,行駛路程為skm,行駛時間為th,填寫下表:(表1)

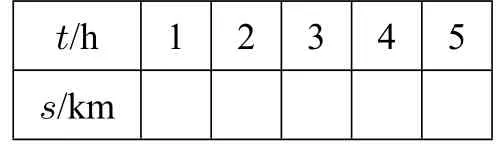
表1

思考: (1)行駛路程隨行駛時間變化而變化,即s隨____的變化而變化;

(2)若汽車行駛th,行駛的路程為skm,則s=____.

(3)當行駛時間t取定一個確定的值時,對應的行駛路程s的取值是否唯一確定?

(例如,當t=10時,s的取值是唯一、還是有多個值?)答:________．

問題3. 圖形問題:你見過水的漣漪嗎?如圖1,圓形水波慢慢地擴大,在這一過程中,當圓的半徑r分別為10cm,20cm,30cm時,圓的面積S分別為多少?

圖1

思考:

(1)圓的面積隨半徑變化而變化,即S隨的變化而變化;

(2)若半徑為rcm,圓的面積為S,則S=____.

(3)當半徑r取定一個確定的值時,對應圓的面積S的取值是否唯一確定?(例如,當t=10時,s的取值是唯一、還是有多個值?)答:________．

設計意圖: 挖掘和利用實際生活中與變量有關的問題情境,讓學生經(jīng)歷探索具體情境中兩個變量關系的過程,直接獲得探索變量關系的體驗.

1.2 交流探索,初步感知函數(shù)

問題1. 上述三個問題中,分別涉及哪些量的關系?通過哪一個量可以確定另一個量?

問題2. 請具體指出上面這些問題中,哪些量是變量,哪些量是常量.

問題3. 在前面的每個問題中,有幾個變量?同一個問題中的變量之間有什么聯(lián)系?

在學生充分發(fā)表自己意見的基礎上師生歸納:上面的每個問題中的兩個變量互相聯(lián)系,當其中一個變量取定一個值時,另一個變量就有唯一確定的值.并給出函數(shù)概念.

(結合函數(shù)概念的形成,老師同步PPT展示函數(shù)的史料)

數(shù)學史料1——函數(shù)的萌芽階段

公元前4000年左右就有了函數(shù)最原始的形態(tài)．14世紀法國數(shù)學家奧雷姆在表示隨時間t而變化的變數(shù)x時畫出圖形,其中心思想就是用圖形來表示一個變量的本質(zhì),它依賴于另一個量．17世紀,這種方法被天文學家開普勒和伽利略應用于天體運行方面的研究,伽利略關于自由落體等的研究始終包含著兩個量同時變化的思想,這些語言被視為早期函數(shù)的雛形．函數(shù)一詞最初出現(xiàn)在萊布尼茨寫于1673年的手稿中,它用來表示任何一個隨著曲線上的點變動而變動的幾何量．1714年,萊布尼茨在《微分學的起源與歷史》中,用“函數(shù)”一詞來表示依賴于一個變量的量．1748年,大數(shù)學家歐拉在《無窮分析引論》中下的函數(shù)定義為:“一個變量的函數(shù)是由該變量和一些數(shù)或常量以任何方式組成的解析式[3]．

設計意圖:在數(shù)學史上,數(shù)學家們對函數(shù)的最初認識就是從兩個相互依賴的量開始,認為函數(shù)就是由一個變量依賴于另一個變量的解析式,而我們學生在初中所學的函數(shù)概念就是這樣一個變量說,因此學生對這3個例子是完全熟悉的,也是能理解的．選材既貼近學生的生活,符合學生的認知發(fā)展,降低理解難度,又遵循了人類歷史上對函數(shù)的認識過程,即數(shù)學家最先認識到的是兩個變量的函數(shù)關系．數(shù)學史的引入使學生的認知更豐盈．

1.3 動手實驗,加深體驗

問題1. 如圖2,是撫順春季某一天的氣溫T隨時間t變化的圖象,看圖回答:

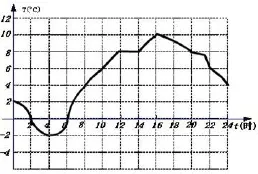
圖2

(1)這天的 8時的氣溫是____℃,14時的氣溫是______℃,22時的氣溫是___℃;

(2)這一天中,最高氣溫是____℃,最低氣溫是____℃;

(3)這一天中,在4時～12時,氣溫( ),在12時～14時氣溫( ),在16時～24時,氣溫( ).

A.持續(xù)升高 B.持續(xù)降低 C.持續(xù)不變

思考:

(1)天氣溫度隨的變化而變化,即T隨____的變化而變化;

(2)當時間t取定一個確定的值時,對應的溫度T的取值是否唯一確定?

(例如,當t=12時,所得溫度T的取值是唯一、還是有多個值?)答:_______．

問題2.表2,我國人口數(shù)統(tǒng)計表中,年份與人口數(shù)可以分別記作兩個變量x與y,對于表中每一個確定的年份x,都對應著一個確定的人口數(shù)y嗎?

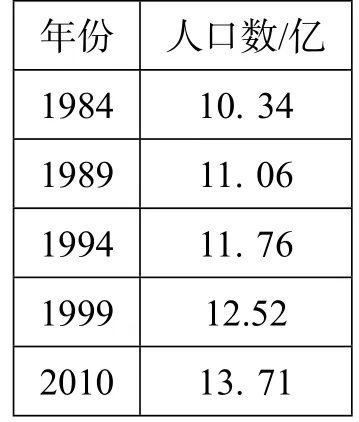
表2

問題3.用10米長的繩子圍成一個矩形,當矩形的一邊長x分別為3米,3.5米,4米時,它的鄰邊長y分別為多少?y的值隨x的值的變化而變化嗎?對于x的每一個確定的值,y都有唯一確定的值與其對應嗎?

問題4. 指出以上問題中的常量、變量,每個問題分別有幾個變量?在每一個問題中,哪個是自變量?你能將其中的某個變量看成是另一變量的函數(shù)嗎?(隨著問題的提出,老師同步PPT展示函數(shù)的史料)

數(shù)學史料2——函數(shù)的發(fā)展階段:

就在歐拉給出函數(shù)的解析式定義不久,他自己也發(fā)現(xiàn)了其局限性,認為圖2、表2這類雖寫不出變量間的解析式,但仍是兩變量間的相互依賴關系,也應該是函數(shù)．于是在1755年的《微分學原理》序言中,歐拉給出了更一般的定義:如果某些量依賴于另一些量,當后面這些量變化時,前面這些變量也隨之變化,則前面的量稱為后面的量的函數(shù)．這里,歐拉明確地表述了變量之間相互依賴的變化關系,使人們對函數(shù)概念的認識在嚴密性上前進了一大步,它反映了數(shù)學對現(xiàn)實關系的摹寫上的進化．

設計意圖: 來自于實際生活中的三個例子,學生能理解．在學生的心中,最開始跟大多當年的數(shù)學家起初的認識一樣,以為函數(shù)必須要有解析式,否則就不是．而圖2,表2的例子就給了學生直觀的沖擊,雖變量間寫不出解析式,但仍有依賴關系,這樣開始過渡到“對應”的思想,讓學生更深刻地體會到函數(shù)對應關系的表示方法有解析式法、圖象法、列表法,有利于學生正確地掌握函數(shù)概念．數(shù)學史料引起學生的共鳴,讓學生在與史上數(shù)學家相同的經(jīng)歷中加深對概念的理解．

1.4 概念辨析,深化理解

問題1. 如表3,是某班同學一次數(shù)學測試中的成績登記表:這一數(shù)學測試中,

表3

(1)13號的成績?yōu)開__;

(2)17號的成績?yōu)開__;

(3)23號的成績?yōu)開___．

思考:

(1)任意確定一個學號x,對應的成績f的取值是否唯一確定?

(2)測試成績隨____的變化而變化;其中常量是,變量是,是自變量,是的函數(shù);

(3)任意確定一個成績f,對應的學號x的取值是否唯一確定?

(4)x是f的函數(shù)嗎?

問題2.兩個變量x、y滿足關系式|y|=x,填表并回答問題:

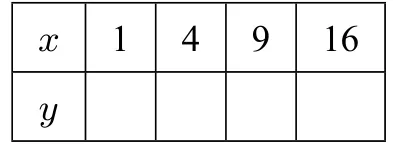
表4

y是x的函數(shù)嗎?為什么?

(隨著問題的發(fā)展,老師同步PPT展示函數(shù)的史料)

數(shù)學史料3——函數(shù)的完善階段:

1837年德國數(shù)學家狄利克雷給出了函數(shù)的定義:“設a、b是兩個確定的量,x是可取a、b之間一切值的變量.如果對于每一個x,有唯一的y值與它對應,使得當x從a到b連續(xù)變化時,y=f(x)也逐漸變化,那么y就稱為該區(qū)間上x的一個連續(xù)函數(shù)．”這就是人們常說的函數(shù)的經(jīng)典定義．這種“對應”的說法,清晰完美地刻畫地函數(shù)兩變量之間的關系. 20世紀初誕生的集合論徹底改變了人們思考問題的方式,以美國數(shù)學家維布倫為代表,結合康托的集合論給出了如今普遍認同的函數(shù)定義:給定兩個集合A和B,如果集合A中的每一個元素在結合B中都有唯一確定的元素與之對應,則稱集合A和B之間的對應關系為從集合A到集合B的函數(shù).

函數(shù)概念的發(fā)展由最初的“解析式”到“變量說”到“對應說”,最后抽象為現(xiàn)在的“關系說”．在這個過程中,函數(shù)概念的抽象程度、嚴密性不斷提高.從函數(shù)概念的歷史來看,經(jīng)歷從感性到理性,從具體到抽象,從常量到變量,思維由具體到抽象的過程,不斷反復、螺旋上升,反映了過程和對象不斷統(tǒng)一的過程．

設計意圖:源自于實際生活的表3,引發(fā)了學生的進一步思考,幫助學生認識函數(shù)概念的本質(zhì).問題1是學生熟悉的生活情景,在理解上沒有難度,具體生動的例子,可以幫助學生理解函數(shù)概念“單值對應”這一核心內(nèi)涵,有助于正確掌握函數(shù)概念.數(shù)學史的介紹讓概念有血有肉,有利于學生理解,也對學生進行了情感教育,培養(yǎng)學生良好的數(shù)學品質(zhì).

1.5 例題解決,運用概念

例1.汽車油箱中有汽油50L,如果不再加油,那么油箱中的油量y(單位:L)隨行駛路程x(單位:km)的增加而減少,耗油量為0.1L/km.

(1)寫出表示y與x的函數(shù)關系的式子;

(2)指出自變量x的取值范圍;

(3)汽車行駛200km時,油箱中還有多少汽油?

設計意圖:鞏固變量與函數(shù)的概念,讓學生充分體會到許多問題中的變量關系都存在著函數(shù)關系,初步接觸函數(shù)的不同表示方法.

1.6 學以致用,鞏固概念

1.購買一些簽字筆,單價3元,總價為y元,簽字筆為x支,根據(jù)題意填表:

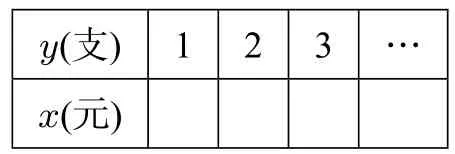
y(支) 1 2 3…x(元)

(1)y隨x變化的____,關系式y(tǒng)=____,____是自變量, ___是___的函數(shù);

(2)當購買8支簽字筆時,總價為___元.

2.周末,小李8時騎自行車從家里出發(fā),到野外郊游,16時回到家里.他離開家后的距離s(千米)與時間t(時)的關系如圖3.

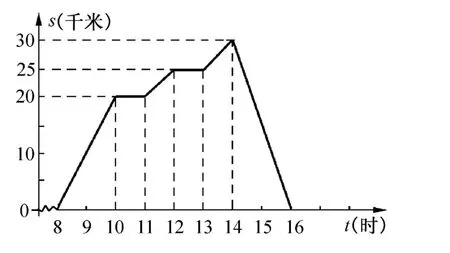
圖3

(1)當t=12時,s=___;當t=14時,s=___;

(2)小李從___時開始第一次休息,休息時間為小時,此時離家____千米.

(3)距離是時間t的函數(shù)嗎?

(4)時間是距離的函數(shù)嗎?

設計意圖:鞏固變量與函數(shù)等概念,讓學生充分體會到許多問題中的變量關系都存在著函數(shù)關系,隱含在函數(shù)關系中表示兩個變量的對應關系有解析法、列表法、圖象法.練習2(4)幫助學生進一步理解函數(shù)的“單值對應關系”,讓學生明確“由哪一個量能唯一確定另一個量”,從而更好地理解自變量與函數(shù)的關系,養(yǎng)成學生逆向思維的習慣．

1.7 小結:函數(shù)的概念

設計意圖:通過小結,讓學生抓住理解函數(shù)概念的實質(zhì)．

2.教學思考

2.1 準確定位,精心預設,生成概念

俗話說:一臺好戲,一定有一個精彩的劇情．課堂是一個舞臺,要使劇情精彩,教師就得定位準,精心設計．本節(jié)課是函數(shù)入門課,首先必須準確認識變量與常量的特征,初步感受到現(xiàn)實世界各種變量之間聯(lián)系的復雜性,研究兩個變量之間的特殊對應關系,同時感受數(shù)學研究方法的化繁就簡．因此本節(jié)課把教學重點放在認識“兩個變量間的特殊對應關系:由哪一個變量確定另一變量”．另一方面,變量與函數(shù)的概念把學生由常量數(shù)學的學習引入變量數(shù)學學習中,較為抽象,學生初次接觸函數(shù)的概念,難以理解定義中“唯一確定”的準確含義．但是,考慮到學生在日常生活中也接觸過函數(shù)圖象、兩個變量的關系等生活實例．所以,在本節(jié)課的教學中,教師優(yōu)化教材內(nèi)容,精心設計教學活動,由實例展開,以問題導線,從學生較為熟悉的現(xiàn)實情景入手,引領學生認識變量和函數(shù)的存在和意義,體會變量之間的互相依存關系和變化規(guī)律,初步理解函數(shù)的概念．借助生活實例,引導學生辨析兩個變量的關系中,由哪一個量的變化引起另一個量的變化,進而指出由哪一個變量確定另一個變量,初步體會函數(shù)概念的核心,正確掌握概念．并結合概念的學習引進史料,還原數(shù)學家們建立數(shù)學概念的火熱思考．課堂在教師的精心設計下,環(huán)環(huán)相扣,遵循函數(shù)概念的發(fā)展,給學生創(chuàng)造了函數(shù)概念發(fā)生發(fā)展的過程,在問題的導線下,層層深入理解,生成概念,剖析內(nèi)涵,掌握概念的本質(zhì)．

2.2 在HPM視角下,激發(fā)學習動力,探究概念形成

章建躍老師說過,概念教學的核心是:讓學生經(jīng)歷概念本質(zhì)特征的概括過程,使學生有機會通過自己的觀察與思考,從具體事例中抽象出概念的本質(zhì)特征進而獲得概念,因此,在概念教學中,要通過恰當?shù)膯栴}情境啟發(fā)學生思考,讓他們經(jīng)歷概念本質(zhì)特征的抽象過程[5]．在歷史上,函數(shù)概念的形成經(jīng)歷了非常漫長的過程,才逐步發(fā)展到現(xiàn)在相對較完善的地步．如此長的一個發(fā)展過程,要在一節(jié)課內(nèi)理解掌握,對初中的學生來說是比較困難的．考慮到初中學生的認知特點,又考慮到歷史上對函數(shù)的認識的過程,正好與初中生的認知相吻合,因此,在本節(jié)課教學中,教師運用信息技術播放,把數(shù)學史融入教學,給學生的概念理解搭“手腳架”,帶給學生以認知沖突,引發(fā)學生對新知的需求,使得學生的學習表現(xiàn)不是停留在知識與技能的掌握這一層面,而是進一步達到了在感受函數(shù)的悠久歷史中傳承知識的文化,將“冰冷的美麗”轉化為“火熱的思考”,讓函數(shù)概念的教學厚重而靈巧,有效地促進教學目標的達成．

弗賴登塔爾指出:“我們不應該完全遵循發(fā)明者的歷史足跡,而是經(jīng)過改良過同時有更好引導的歷史過程”．在教學中,教師采用了“動作分解”,精心設計教學環(huán)節(jié),針對函數(shù)概念在產(chǎn)生過程中遇到的幾個問題創(chuàng)設相類似的簡單生活情景,沿著歷史上數(shù)學家探究函數(shù)概念的足跡,把歷史上數(shù)學家對函數(shù)的4次抽象認識,用生活中具體例子來說明,讓學生體驗函數(shù)概念產(chǎn)生的過程,了解數(shù)學知識在歷史上產(chǎn)生的來龍去脈,引領學生參與變量的發(fā)現(xiàn)和函數(shù)概念的形成過程,體會從生活實例抽象出數(shù)學知識的方法,感知現(xiàn)實世界中變量之間聯(lián)系的復雜性,數(shù)學研究從最簡單的情形入手,化繁為簡．這樣使學生既感到直觀,又循序漸進地認識函數(shù),完全符合歷史發(fā)生原理,把數(shù)學史知識隱性地融入到課堂教學中．

2.3 濃妝淡抹,取舍有道

課堂教學也如文章,在哪些環(huán)節(jié)該濃墨淡彩,在哪些地方該取舍,教師需心中有數(shù),把握好詳與略的度,否則易出現(xiàn)“頭重腳輕”或者“浮光掠影”,影響教學的目標的落實．本節(jié)課從整體上分為“情景的引入,概念生成,概念的鞏固與應用,課堂小結”四個板塊,其中概念的形成又經(jīng)歷了“認識變量與常量——初步感知函數(shù)——函數(shù)概念的變量法認知——函數(shù)概念的對應法認知”四個環(huán)節(jié)．在教學中,教師在細節(jié)上精心設置每一個預設的問題,關注學生的學習心理,了解學生思維的最近發(fā)展區(qū),創(chuàng)設情景,讓學生“簡約”地經(jīng)歷概念的生成．同時,在整體上合理分配各板塊和環(huán)節(jié)教學時間,使得整個概念的教學既蘊味深長,又不冗長抽象,符合學生的認知．

[1]吳駿,汪曉勤.數(shù)學史融入數(shù)學教學的實踐:他山之石[J].數(shù)學通報, 2014(2):13-16

[2]數(shù)學·八年級下冊.人民教育出版社,2012

[3]田方琳,汪曉勤.初中數(shù)學課堂上的數(shù)學故事[J].中學數(shù)學月刊, 2013(9)

[4]宋瑛.HPM視角下_函數(shù)的概念_第一課時_的教學與感悟.福建中學數(shù)學,2015(4):5-8

[5]章建躍.如何實現(xiàn)“思維的教學——以平面圖形的旋轉”的教學為例.中學數(shù)學參考,2015(4)10-12