例談定義域在解題中的應用

山東省青州第三中學(262500) 岳洪偉

例談定義域在解題中的應用

山東省青州第三中學(262500) 岳洪偉

函數是高中數學重要內容,貫穿始終,是教學過程中的重點,也是難點.定義域是函數要素之一,占有重要地位,在解題時如果忽視定義域會導致解題錯誤,本文對幾個例題簡要分析,希望在解題時充分重視定義域的重要作用.

一．判斷是否為同一函數

例1:下列各組函數中,表示同一函數的是:( )

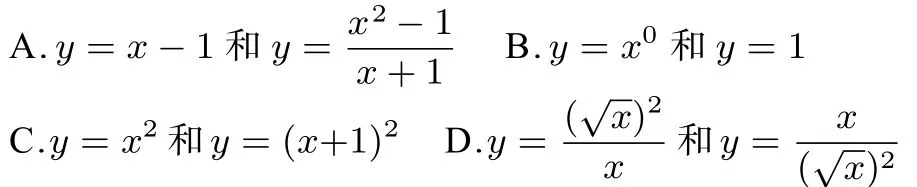
分析:判斷兩個函數是否是同一函數,需要函數的要素對應相同,在A.B選項中兩函數定義域不同,C選項中兩函數對應法則不同,所以正確選項為D,另外需要補充一點,求函數的定義域時,不能對函數的解析式進行化簡、整理之后再求定義域,因為化簡會改變函數自變量的取值范圍,引起定義域錯誤.

二．判斷函數奇偶性

分析:判斷函數的奇偶性的首要步驟就是判斷函數的定義域是否關于原點對稱,如果對稱再判斷f(?x)=±f(x)是否成立,最后得出結論.在題目的四個函數中①先求出定義域為{1,?1},所以關于原點對稱,并且把原函數化簡后得到非常典型的一個函數f(x)=0,既是奇函數又是偶函數.②定義域為R,且所以為奇函數,如果推導時運算比較麻煩也可轉化為判斷f(?x)±f(x)=0是否成立.③求出函數的定義域為(?1,1],不關于原點對稱,所以非奇非偶函數④求得定義域為{x|?2≤x≤2,x/=0},再化簡原函數為顯然為奇函數.通過以上四個小題,特別是在①④兩函數中,定義域還起到了簡化函數解析式的作用,如果不作相應的化簡,會直接導致最后結論錯誤.

三．函數單調性中的應用

例3(2013北京模擬)已知函數其中b∈R,

(1)若x=?1是f(x)的一個極值點,求b的值.

(2)求f(x)的單調區間.

分析:在本題中利用導數得到函數單調性,屬于基本方法,但在第(2)問中很容易把定義域當作R,忽視定義域,從而導致全部單調區間出錯,所以在求函數單調性問題時要把定義域放到首要地位,以防失誤.

四．在函數對稱性中的應用

例4(2016武漢四月調研)函數的對稱中心為( )

A. (?4,6) B. (?2,3)

C. (?4,3) D. (?2,6)

分析:本題可以由定義域進行快速解題,函數的定義域為{x|x/=?1,x/=?2,x/=?3},如果有對稱中心,其定義域也必關于此點對稱,所以此點橫坐標只能為?2,答案選B．

五．解不等式中的應用

例5(2016湖南邵陽月考)已知函數f(x)的導函數f′(x)=5+cosx,x∈(?1,1)且f(0)=0,若f(1?x)+f(1?x2)＜0,則實數x的取值范圍是___

分析: 由條件求得f(x)=5x+sinx,此函數是奇函數,且在(?1,1)上單調遞增,由f(1?x)+f(1?x2)＜0得f(1?x)＜f(x2?1),所以,解得在本題中,不能漏掉原不等式中定義域的要求.

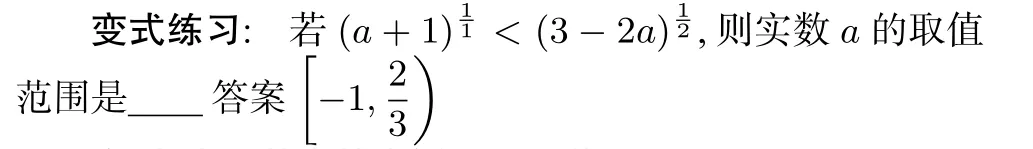
六．復合函數中的應用例6(2016廣西柳州期中)已知函數ax+a)在區間上是增函數,則實數a的取值范圍是___

分析:所給函數為復合函數,根據內外兩層函數單調性“同增異減”原則,只需令g(x)=x2?ax+a在區間上是減函數,且g(x)＞0,所以解得容易遺漏函數定義域要求g(x)＞0導致出錯.

變式練習:若函數f(x)=loga(ax2?x)(a＞0a/=1)在[3,4]上為增函數,則實數a的取值范圍是____答案: (1,+∞)

七．求最值中的應用

例7.已知x2+y2?2y?3=0,求x2+2y2的取值范圍.

分析:由x2+y2?2y?3=0得x2=?y2+2y+3代入x2+2y2得x2+2y2=y2+2y+3=(y+1)2+2,但一定不要漏掉由x2=?y2+2y+3≥0這一隱含條件決定了y的范圍為[?1,3],所以原式取值范圍為[2,18].

八．其它相關的應用

例8. 已知命題p∶α=β,命題q∶tanα=tanβ,則p是q的( )

A．充分不必要條件 B．必要不充分條件

C．充要條件 D．既不充分也不必要條件

通過以上幾個例題,能看出定義域在解題中的重要性,如果忽視了對定義域的研究,很有可能看似簡單題目也會變得漏洞百出,導致失誤丟分,所以在解題中,提高對定義域的的重視,也就會提高解題的正確率,達到事半功倍的效果.