培養中學生數學應用能力的一點做法

廣東省汕頭市潮陽區谷饒中學(515159) 張應武

培養中學生數學應用能力的一點做法

廣東省汕頭市潮陽區谷饒中學(515159) 張應武

數學源于實踐又服務于實踐,數學理論是人們在研究世界的空間形式和數量關系的過程中,通過科學的抽象而逐步發現和發展的,它具有準確性、嚴密性、邏輯性和抽象性等品格,但它之所以能長盛不衰不斷發展,主要還是由于它能用來解決實際問題.在平時的教學過程中,很多老師都有這種感覺:許多學生盡管對解決純數學問題得心應手,然而一旦遇到實際問題便束手無策,而當教師把這些問題轉化為數學模式,用數學語言加以表述后,學生便恍然大悟,很快解決問題.原因就在于數學教學只偏重對具體數學形式和技巧的盲目追求,忽視了對學生應用數學知識能力的培養,使得相當多的中學生未能接受到他們所需要的數學教育.

數學的學習就不僅只是為了升學的需要,而更主要的是為學生的生活和就業提供必要的數學知識和技能.因而在具體的教學實踐中,教師就需要教給學生把實際問題轉化為數學問題的方法,有意識地對學生進行數學實踐能力的培養,使學生能夠學以致用,讓學生真正感受到數學的價值,從而激發他們努力學習數學的興趣和動力.

要培養學生運用數學方法解決實際問題的能力,就要在學生認真掌握好數學基本概念、基本知識和基本技能的基礎上,大力加強數學應用題的教學,培養學生對實際問題進行數學抽象的能力,教會學生把表述實際問題的自然語言翻譯為數學語言.在此基礎上,在適當的時間和適當的場合,介紹數學史上將實際問題轉化為數學問題的一些實例,能大大提高學生學習數學的興趣,激發他們的學習積極性和主動性,使他們的數學應用能力得到進一步強化.現舉例說明.

例1博爾達計分法問題

在一次選舉中,共有四位選民和五位候選人,選民依他們對候選人喜好的程度,將候選人從上到下排列如下表,問哪一個當選?

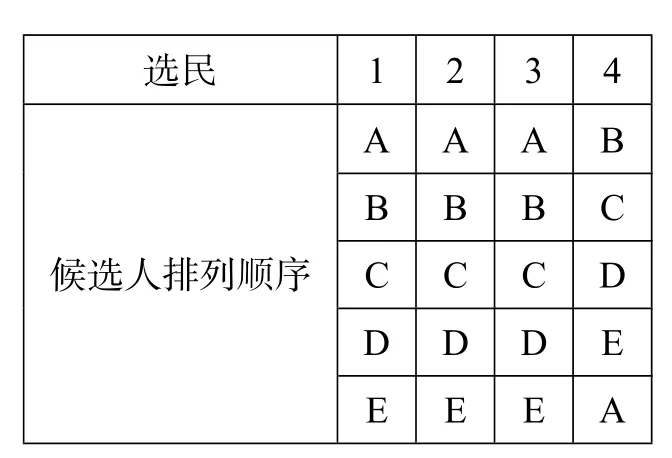
選民1 2 3 4 A A A B B B B C候選人排列順序C C C D D D D E E E E A

解決這個問題主要是要給出理由依據,即把這個問題數學化,也即量化,但如何數學化呢?

1770年法國數學家博爾達(Jean Charles de Borda)提出一套排列候選人順序的計分辦法.博爾達計分法的操作,可用下面的表格來說明.在表格中,共有四位選民和五位候選人,選民依他們對候選人喜好的程度,將候選人從上到下排列,排列在越高位置的候選人,得分越高.

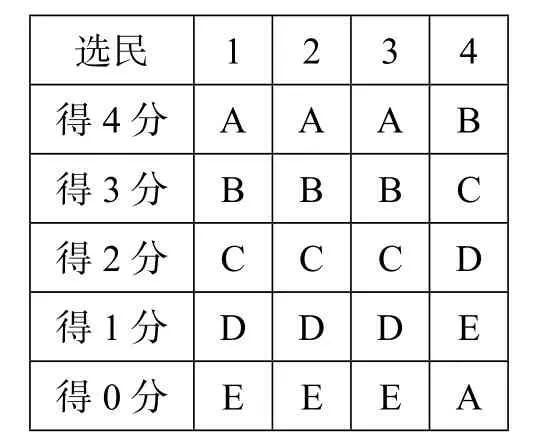
選民1 2 3 4得4分A A A B得3分B B B C得2分C C C D得1分D D D E得0分E E E A

候選人A共得12分,B得13分,C得9分,D得5分,E得1分.因此,根據博爾達計分法,最理想的排列順序是:B, A,C,D,E.

這個問題能推廣到n個村民選舉m個候選人的一般情況,只需把得分修改就行.

這種方法用到的知識不是很高深,但卻能解決問題,即把問題轉化為數學問題,能夠調動學生的學習興趣.這種方法還能夠推廣,如有四只寶馬A、B、C、D進行4輪的比賽,成績如下:

輪次名次①②③④23 B 2 142 C 4 411 D 3 234 A 13

問:哪一只寶馬比較好?

按照博爾達計分法可以這么操作:第一名得3分,第二名得2分,第三名得1分,第4名得0分,則A得7分,B得7分,C得6分,D得4分.A和B的成績一樣.我們可以改變得分:第一名得5分,第二名得3分,第三名得1分,第4名得0分,則A得10分,B得11分,C得10分,D得5分.這樣B是成績最好的.

同樣,這個問題也可以推廣到一般的情況(n只馬進行m次的比賽).

問題還可以推廣到團體的總積分的計算,如計算一個體育代表團的總積分問題(給第一名、第二名、第三名等賦相應的值就可以計算了).

例2哥尼斯堡七橋問題

圖1

在18世紀,普魯士的哥尼斯堡城(現立陶宛共和國)的許多人熱衷于一個難題:在哥尼斯堡鎮有一個島,普雷格爾河兩支繞流其旁,七座橋a,b,c,d,e,f,g跨這兩條支流(如圖1所示).問:一個人怎樣走,才能一次走遍七座橋,且每座都只經過一次.很多人都想解決這個難題,但年復一年,誰也找不到答案.這個問題表面看起來跟數學毫不相干,但是數學大師歐拉卻在1736年用數學方法證明了這樣的走法是不存在的.歐拉的方法非常巧妙,也非常簡單.他發現,在這個問題中A,B,C,D四塊陸地的大小和橋的長短、河的寬窄等都無關緊要,因而A,B,C,D可以抽象為平面上的四個點,而七座橋可以抽象為連接這四個點的線條,如圖3這樣,問題就變為:能否一筆畫出圖3中的圖形,即筆不離紙,每個點、每條線都經過,且每條線都不重復?

歐拉把像圖3那樣由若干個點和連接這些點的若干條線組成的圖形稱為“網絡”,把線的交點叫“頂點”.如果一個頂點有奇(偶)數條線相交,這個頂點就叫做奇(偶)點.歐拉證明了:一個網絡能夠一筆畫出的充要條件是該網絡中奇點的個數是0或2.顯然,圖3中4個頂點都是奇點.所以圖3不可能一筆畫出來,即滿足原題中條件的走法是不存在的.這種方法導致了一門嶄新的數學分支——圖論(起初歐拉稱為位置幾何學)的誕生,也為拓撲學的建立奠定了基礎.圖論和拓撲學的發展,又為生產、生活和科學研究中的各種新問題的解決提供了強有力的數學工具.

例3斯坦納最短距離問題

1 9世紀的德國數學家斯坦納根據生產實踐的需要,研究了一個看起來雖然簡單,但卻很有實用價值的問題:在三個村莊之間建立一個供水站,為了讓用水的人方便,并且所用水管最省,問:怎樣確定供水站的位置?

換成數學語言就是:設A,B,C是平面內不在同一直線上的三點,求△ABC內的一點M,AM+BM+CM最小.

這個問題還可以推廣為:在A,B,C三個村莊間建一座供水站,已知通往各個村莊的水管造價分別為(單位:元／米)m,n,r,問供水站應建在何處,才能使總造價最低?換成數學語言就是,在△ABC內求一點M,使mAM+nBM+rCM最小.

問題還可變化為:設A,B,C三個村莊分別有學生200人,300人,400人要在三個村莊間建立一所學校M,使所有學生在上學時所走的總路程最短.

換成數學語言就是:在△ABC中求一點M,使200AM+300BM+400CM最小.

盡管上述三個問題各有不同的實際意義,但化為數學語言后可以看出,它們的實質都是同一個數學問題:設m,n,r為常數,在△ABC內求一點M,使mAM+nBM+rCM最小.第一個問題是的特殊情形.

數學的強大功能之一,就在于它能將形式各異的實際問題抽象出共同的本質特征,而用相同的數學方法來解決不同的實際問題,如何從自然語言到數學語言是轉換的關鍵,在于把三個村莊、供水站或學校抽象為平面上的三個已知點和一個未知點;把連接村莊的水管或學生所走的路徑,抽象為連接點的線段.實際問題化為數學問題,就能夠運用相應的數學知識加以解決.

從以上幾個實例可以看出,把實際問題轉化為數學問題的關鍵,在于把表述實際問題所用的自然語言翻譯成數學語言.而要做到這一點,就需要進行相應的數學抽象.

此外,還可以向學生介紹“航船相遇問題”、“韓信點兵”、“獄吏問題”和其他典型例題,也能大大激發學生學習數學的興趣和動機,改變他們對數學“抽象”、“神秘”、“無用”的看法,消除他們對解決應用題的畏難情緒,讓他們轉而迷戀應用題,從而形成數學學習的良性循環.

日本教育家杉山吉茂先生說過:“數學帶有人類社會有價值的東西,因此數學必須有用途和益處,這種用途和益處本來是應該教應該學的,可是在教學過程中往往忘掉這一點而陷入技能的熟練之中,使人感到數學是討厭的、是與自身無關的思維游戲而已”.數學的教學實踐說明,教師在教學中充分注意引導學生去追求數學的價值和美,必定能夠促使學生對數學產生極大的學習欲望,而不再停留于為應付升學考試去死記硬背數學概念、公式、定理.這樣,無論他們將來繼續升學與否,數學都會使他們受益終生.

[1]張卿,妙趣橫生的數學難題[M],天津:天津人民出版社,1980.