向量表示：一種重要的數(shù)學問題解決思想

楊越

[摘 要] 向量具有豐富的物理背景，也是幾何與代數(shù)的研究對象，是溝通幾何與代數(shù)的橋梁的重要數(shù)學模型. 在高中數(shù)學中，向量是一個較為特殊的核心概念. 本文結(jié)合高中數(shù)學應用向量思想方法解決數(shù)學問題的三種主要表示形式，具體分析了利用向量表示優(yōu)化解題的一般策略. 它將突出向量的工具性作用與解題的簡潔性特點，能夠有效地培養(yǎng)數(shù)學的創(chuàng)造性思維品質(zhì).

[關(guān)鍵詞] 向量；向量表示；高中數(shù)學

數(shù)學思想，是數(shù)學內(nèi)容的精髓，是知識轉(zhuǎn)化為能力的橋梁. 向量具有豐富的物理背景，它同時也是幾何與代數(shù)的研究對象，是溝通幾何與代數(shù)的橋梁的重要數(shù)學模型思想. 在高中數(shù)學中，向量是一個較為特殊的核心概念. 一方面，向量具有方向、位置、長度、夾角等“形”的特征；另一方面，向量亦具有大小、正負、能像數(shù)一樣運算等“數(shù)”的屬性. 為了突出向量這一形數(shù)兼?zhèn)涞摹岸匦浴保壳敖滩闹邢群筇峁┝巳N不同的表示方法：幾何表示、數(shù)乘表示與坐標表示. 這些向量表示思想方法不僅深刻地揭示了向量知識的本質(zhì)屬性，其蘊含的數(shù)學思想也為我們理解數(shù)學問題與優(yōu)化解題策略提供了更加廣闊的思維發(fā)展空間.

[?] 向量的表示形式

在數(shù)學上，一個數(shù)學對象可以用某一特定的形式來表示，也可以用與其特定形式等價的另一種形式來表示. 對數(shù)學對象的思維、操作和運算是借助于它的表示形式來實現(xiàn)的. 適合的表示形式不僅能夠直觀地反映數(shù)學對象的特征，也有助于研究、建構(gòu)數(shù)學對象之間的結(jié)構(gòu)和關(guān)系. 對于向量，為了表示其有向線段的特性，通常用符號或a來表示. 此外，對于某一特定的非零向量而言，還有如下三種表示形式.

幾何表示：向量可以表示為向量與的和，或向量與的差，即=+或=-. 向量的幾何表示遵循平行四邊形法則或三角形法則，其實質(zhì)是，對某一特定向量，可以通過兩個不同向量的組合來實現(xiàn). 向量的幾何表示反映了向量在方向、位置等“形”的方面的關(guān)系和屬性，突顯向量作為“有向線段”與“線段”的根本差異.

數(shù)乘表示：向量可以表示為與其平行的單位向量e與一個常數(shù)的乘積，即若向量的長度為k，則向量=ke. 在此基礎上，我們可以進一步得出，平面上的任一非零向量都可以表示為兩個單位向量的線性組合，即存在兩個單位向量e1，e2，使得=k1e1+k2e2. 向量的數(shù)乘表示形式直觀地反映了向量在大小和方向兩個方面的特征.

坐標表示：以向量的始點A為坐標原點建立平面直角坐標系，若設向量在x軸、y軸上的投影坐標分別a，b，則向量=（a，b）. 向量的坐標表示實現(xiàn)了“形”與“數(shù)”的完美統(tǒng)一，即一個有向線段和一對有序?qū)崝?shù)對之間存在一一對應關(guān)系，實現(xiàn)了從“形的推理”到“數(shù)的運算”的轉(zhuǎn)換.

三種表示形式試圖從“形”和“數(shù)”兩方面揭示向量的本質(zhì)屬性. 幾何表示強調(diào)向量的“形”，可以刻畫直線、平面、空間等幾何對象的位置關(guān)系和度量性質(zhì). 坐標表示強調(diào)向量的“量”，可以參與代數(shù)運算. 數(shù)乘表示則二者兼具. 另外，三種表示形式之間并非完全獨立，而是可以相互轉(zhuǎn)化. 例如，在坐標表示中引入單位向量，即設x軸、y軸上的單位向量為i， j，則=（a，b）=ai+bj. 同樣，在幾何表示中引入單位向量，則可以實現(xiàn)幾何表示與數(shù)乘表示的轉(zhuǎn)換. 需要指出的是，上述二維平面的向量表示很容易推廣到三維空間的向量表示.

[?] 利用向量表示優(yōu)化解題策略

向量是數(shù)形結(jié)合的化身. 向量表示實現(xiàn)了從“形”到“數(shù)”或者從“數(shù)”到“形”的轉(zhuǎn)化，為解決數(shù)學問題提供了強有力的工具. 適當選擇向量的不同表示形式，將代數(shù)問題幾何化，或者將幾何問題代數(shù)化，有助于揭示數(shù)學問題背后所隱藏的數(shù)量關(guān)系、幾何特征，理解數(shù)學問題的實質(zhì)，優(yōu)化解題策略. 下面舉例說明利用向量表示解決問題的一般策略.

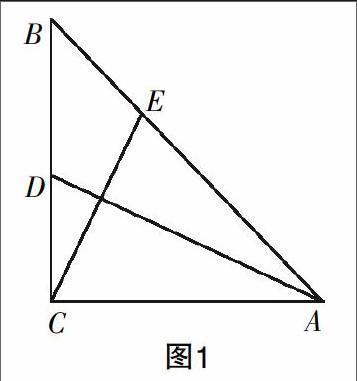
證明：根據(jù)向量的數(shù)量積，若兩個非零向量的數(shù)量積為0，則這兩個向量相互垂直. 要證AD⊥CE，即證明·=0成立即可. 為此，設CA=CB=m，注意到=+，=-，

于是·=（+）（-）=·-·+·-·

=m·m·-m·m·1+m·m·+m·m·0

=m2-m2+m2+0=0.

即·=0. 根據(jù)向量乘法性質(zhì)可知，AD⊥CE.

上述證明的關(guān)鍵是，用向量表示問題所涉及的幾何元素，將幾何問題（AD⊥CE）轉(zhuǎn)化為向量問題（·=0）. 通過向量運算，特別是向量的數(shù)量積運算，研究幾何元素之間的關(guān)系，如垂直、平行、長度、角度等. 最后利用向量數(shù)量積的性質(zhì)對運算結(jié)果做出幾何解釋.

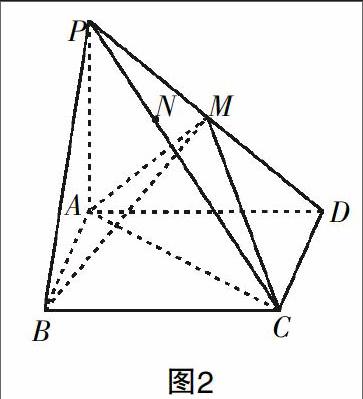
例2：如圖2，在四棱錐P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2. 以AC的中點O為球心、AC為直徑的球面交PD于點M.

（1）求證：平面ABM⊥平面PCD；

（2）求直線CD與平面ACM所成的角的大小.

解：以A為坐標原點，AB，AD，AP所在的直線分別為x軸、y軸、z軸建立空間直角坐標系. 于是，A（0，0，0），B（2，0，0），D（0，4，0），P（0，0，4）.

（1）平面ABM⊥平面PCD的問題可以轉(zhuǎn)化為證明PD與AB，AM或BM垂直的問題.

由于=（0，4，-4），=（2，0，0），=（0，2，2），

于是·=0，·=0，即PD⊥AB且PD⊥AM，

所以PD⊥平面ABM.

因為PD?平面PCD，

所以平面ABM⊥平面PCD.

（2）求直線CD與平面ACM的夾角可以轉(zhuǎn)化為求直線CD與平面ACM的一條垂線所成的角.

設平面的法向量為n=（x，y，z），注意到=+=（2，0，0）+（0，4，0）=（2，4，0）.

根據(jù)n⊥且n⊥，得n·=（x，y，z）（2，4，0）=2x+4y=0 ①.

且n·=（x，y，z）（0，2，2）=2y+2z=0 ②.

聯(lián)立①②求解，且取y=1，得法向量n=（-2，1，-1）.

設所求的夾角為α，于是可得cosα====.

所以直線CD與平面ACM的夾角是arccos.

利用向量表示，將幾何對象向量化、數(shù)量化，最終運用代數(shù)運算處理面面、線線、線面等位置關(guān)系和度量性質(zhì)的基本思路. 與幾何方法相比，向量法是一種較為程序化的方法，其關(guān)鍵在于建立適當?shù)淖鴺讼挡⒂孟蛄勘硎酒渲械挠嘘P(guān)對象，進而將幾何的推理轉(zhuǎn)化為代數(shù)的運算.

例3：證明不等式+≥（m+n）2當0

證明：由a，b的數(shù)量積a·b=

可知，≥m+n>0.

所以+≥（m+n）2，當且僅當a∥b，即=時等號成立.

[?] 研究小結(jié)

代數(shù)符號的抽象表達有時構(gòu)成了理解和解決問題的障礙. 對于諸如不等式、函數(shù)最值、解析幾何、三角函數(shù)等一類解證問題，如果我們能夠構(gòu)造向量表示其中的數(shù)量關(guān)系，再借助于向量的幾何直觀或者運算性質(zhì)，就容易發(fā)現(xiàn)或找到解決問題的思路和突破口，達到優(yōu)化解題過程、降低解題難度的目的.

向量集“數(shù)”“形”于一身，是高中數(shù)學最基本的概念之一. 作為“數(shù)”，向量具有代數(shù)的一些運算性質(zhì)；作為“形”，向量具有幾何的直觀推理屬性. 因此，向量是數(shù)形結(jié)合思想的一般體現(xiàn)，是實現(xiàn)幾何問題與代數(shù)問題相互轉(zhuǎn)化的中介. 作為一種思想方法，向量法解決問題的關(guān)鍵在于用適當?shù)南蛄勘硎酒渲械臄?shù)學對象，從而將幾何問題或代數(shù)問題轉(zhuǎn)化為向量問題，進而利用向量的代數(shù)運算或直觀推理獲得問題的解答. 用向量表示解決數(shù)學問題的一般步驟可以歸納如下（見圖3）：

[數(shù)學問題][向量問題][解 答][向量

表示] [代數(shù)運算] [直觀

推理]

圖3

概括起來，應用向量數(shù)學思想來解決問題，其目的是突出向量的工具性作用，發(fā)揮向量思想方法解題的簡潔性和優(yōu)越性的特點，在解題過程中發(fā)現(xiàn)數(shù)學原型，建立起更新的數(shù)學模型，推動數(shù)學學科發(fā)展，更主要的是可以有效地培養(yǎng)學生的數(shù)學創(chuàng)造性思維能力，提升數(shù)學學習的品質(zhì).