讓學生動手做數學

翁娟娟

[摘 要] 線段、射線、直線是最簡單、最基本的幾何圖形，本節內容是初中幾何基礎中的基礎，起著奠基的作用. 筆者通過分析教材，結合教學實際做課例評析.

[關鍵詞] 課堂教學；動手做數學；實錄；評析

教材分析

《標準》對此內容的要求是：理解兩點間的距離的意義，能度量兩點間的距離；掌握“兩點之間線段最短”“兩點確定一條直線”的基本事實. 教科書圍繞《標準》要求，設置了“議一議：走哪條路線相對近一點？以點A為一個端點的線段有哪些？……線段之間有怎樣的關系”“試一試：走下列哪條路徑更近？過點A可以畫幾條直線？經過A，B兩點可以畫幾條直線”以及“練一練”等教學素材，其目的是有效落實《標準》中“推理能力的發展應貫穿于整個數學學習過程中”的基本要求，并遵循小步子、多層次原則，采用由易到難、由淺入深地逐步發展學生的演繹推理能力的方法來開展幾何教學.

教學目標及解析

1. 理解線段、射線、直線等圖形，并會用符號表示.

2. 借助具體情境和動手操作，掌握兩個基本事實：兩點之間線段最短，兩點確定一條直線.

重點：線段、射線、直線的表示方法，理解兩個基本事實.

難點：線段、射線、直線的圖形語言、符號語言以及文字語言的相互轉化.

教學中要在學生的認知特點和知識的發展水平的基礎上，培養他們的動手、動口、動腦及相互合作的能力，為系統學習幾何知識積累寶貴的經驗.

“6.1線段、射線、直線”（第一

課時）教學過程簡錄

片段一：兩個基本事實

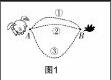
師：運用線段、射線、直線的相關知識回答問題——如圖1，小兔想從A地到B地，圖1中的哪一條相對近一點？有沒有最短的路線？請在圖中畫出來.

生1：第②條路線相對近一點，最短的路線應該是把A，B連起來.

師：連起來是什么意思？請上來演示一下.

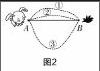
（生1將其連了起來，如圖2）

師：連成的是什么圖形？它有長度嗎？

生1：應該將A，B連成線段，則線段AB就是小兔走的最短路線.

師：你能否將上述生活常識總結成一條數學結論？

生1：在兩點之間，直線比彎的線短.

師：直線有長度嗎？彎的線是什么意思？

生1：應該是在兩點之間所有的線中，線段最短.

師：兩點之間，線段最短，這是一個基本事實，可以直接用于解決問題.

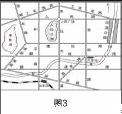
師：觀察地圖（如圖3），火車站到汽車站的兩條路線中，走哪條路線最近？請說明理由.

生2：應該是青年路更近一些，因為剛學過“兩點之間，線段最短”.

師：很好！說明問題時，我們要學會有依據地說明問題.

師：在數學上，把“兩點之間線段的長度叫做這兩點之間的距離”.

師：線段主要是從圖形的角度來認識問題的，距離主要是從數量的角度來認識問題的，數學常把圖形與數量結合起來研究.

（做一做：測量北京、天津、上海、重慶四個直轄市之間的距離）

師：經過一點O畫直線，能畫幾條直線？經過兩點A，B呢？經過三點A，B，C呢？由此，你可以能到什么結論？

師：（巡視活動情況，引導學生總結出直線的性質）經過兩點有一條直線，并且只有一條直線，簡述為兩點確定一條直線.

（強調直線的“唯一性”和“存在性”）

師：如果你想將一根細木條固定在墻上，至少需要幾個釘子？有什么依據？

生3：至少需要2個釘子，因為兩點確定一條直線.

師：日常生活中有哪些做法應用了直線的性質？

（生舉例）

評析？搖 創設讓小兔選擇路線的問題情境，一是鞏固“兩點之間，線段最短”的數學事實，二是為講授“兩點間的距離”的定義作鋪墊. 設計“做一做”的目的，一是鞏固小學學過的讀句畫圖的能力，二是通過畫圖活動讓學生反思操作過程，得到“兩點確定一條直線”. 上述問題都是生活中學生經常遇到的問題，學生解決生活中的數學問題，一是進一步鞏固和理解兩點之間的距離的意義和“兩點確定一條直線”的基本事實，二是主動參與學習過程，培養動手動腦的能力，并在活動中初步體會數學是解決實際問題和進行交流的重要工具.

片段二：直線、線段、射線的表示方法

師：我們知道了直線的概念，認識了直線，那么如何表示直線呢？

方法一：根據基本事實“兩點確定一條直線”，可用直線上的任意兩點來表示直線（注意表示點的字母必須大寫，如圖4）.

方法二：用一個小寫字母來表示一條直線.

（直線的表示方法如圖4）

注意：語言要寫完整. 例如直線AB（或直線BA），不要寫成AB，BA；直線l不要寫成l.

師：如何表示一條線段？

生4：我認為有兩種表示方法，線段AB或線段BA；線段a，如圖5.

師：你是怎么想到的？

生4：參照直線的表示方法.

師：你用類比的思維來認識這個問題，很好！類比是解決問題很有效的思維方式. 那如何表示一條射線呢？

生5：射線AB或射線BA；射線a.

師：由于射線是有方向的，所以只能用兩個大寫字母來表示，通常把射線端點的字母寫在前面. 如射線AB. 要注意，射線AB和射線BA不是同一條射線.

（射線的表示方法如圖6）

師：在平面上，點和直線有怎樣的位置關系？

（引導學生討論，得出：點在直線上，點在直線外）

例題？搖 如圖7，點B，C在線段AD上.

（1）圖7中以點A為一個端點的線段有哪幾條？以點B為一個端點的線段有哪幾條？

（2）圖7中共有幾條線段？是哪幾條？

注意：線段的兩個端點中，只要有一個端點不同，就表示不同的線段；注意分類討論思想的運用，注意不重復、不遺漏.

變式？搖 往返南京、上海兩地的城際高鐵，中途必須停靠鎮江、無錫、蘇州站，根據你所學的數學知識回答：需要制定多少種不同的票價？

評析 直線的表示方法，只能用講授的方式來傳授，必須向學生講清楚用兩個大寫字母表示直線的合理性. 學生已有用一個大寫字母來表示一個點的基礎，再加上剛學的“兩點確定一條直線”的基本事實，就能說清楚兩個大寫字母來表示一條直線的合理性，這也是把“兩點確定一條直線”前置到“線段、射線、直線的表示法”之前的意圖. 在此基礎和經驗上，提出“線段、射線該如何表示”，其意圖是讓學生用類比直線的表示方法，自認得到線段、射線的表示方法. 需要注意的是，表示射線時，教師需說明白把射線的端點字母寫在前面這一規定的合理性. 設計中把“點與直線的位置關系”提出來讓學生討論，居于以下認識：一是點與直線的位置關系雖沒多大的實際價值，但它是初中幾何最基本的位置關系，為后面（直）線（直）線關系、點與圓、直線與圓關系形成一個完整的系統. 圖7的問題是書上的例題，主要是讓學生有條理地研究問題，并積累一些經驗. 變式主要是讓學生明白數學上往往存在“形異實同，形同實異”的問題.

教學反思

本案例通過設計數學活動及問題鏈的形式，讓學生學會探索、學會發現. 借助多媒體演示、實物等，學生憑借生活經驗及幾何直覺對所要討論的問題有了直觀的感性認識，發現“兩點之間，線段最短”的事實，通過畫圖操作等數學活動，發現“兩點確定一條直線”的事實. 此教授過程不是把學習材料直接呈現給學生，而是通過問題啟發，學生通過積極主動地探索活動來學習知識，掌握策略，提高學生的實踐、探索能力，體現“讓學生動手做數學”的基本理念.