掌“數”舵　揚“形”帆　讓思維啟航

福建省松溪縣實驗小學　潘　麗

掌“數”舵揚“形”帆讓思維啟航

福建省松溪縣實驗小學潘麗

數形結合思想是一種重要的數學思想。在教學中滲透數形結合的思想，可去偽存真、化繁為簡、化解學習難點。在解決問題的過程中，可提高學生的思維能力和數學素養。適時的滲透數形結合的思想，可達到事半功倍的效果。

小學數學數形結合滲透

“數”與“形”是貫穿整個小學數學教材的兩條主線，是貫穿小學數學教學始終的基本內容。我們在研究抽象的“數”的時候，往往要借助直觀的“形”，在探究“形”的性質時，又往往離不開“數”。利用數形結合能使“數”和“形”統一起來，以形助數、以數輔形，讓數與形各展其長，相輔相成，使許多數學問題變得簡易化。本文將結合課堂教學實例談談如何在教學中有效滲透數形結合的思想。

一、數形結合——去偽存真，把握概念本質

對于抽象的概念，小學生基本上處于感性直觀的認識階段。數形結合能使比較抽象的概念轉化為清晰、具體的事物，讓學生經歷“將豐富的感性材料加以去粗取精、去偽存真、由表及里”的改造過程，從而讓學生更好地發現概念的本質屬性。

請看泉州師院附小謝玉娓老師《倍的認識》教學片段：

師：慢羊羊村長用實心小棒擺了一個正方形。數一數用了幾根小棒？（4根）

師：如果用空心小棒也擺這樣一個正方形，需要幾根？（4根）

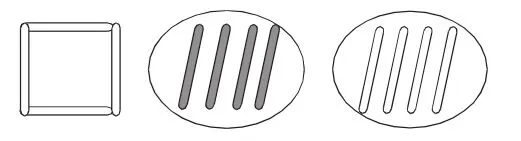
師：也就是要用上1個4。如果我們把4根實心小棒看作一份，空心小棒也是這樣的一份，每一份都是4根。瞧，美羊羊又擺了一份空心小棒。

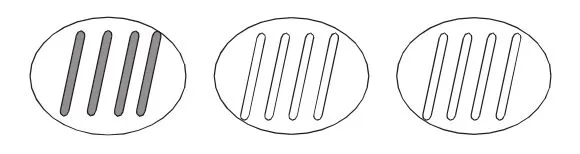
師：請同學們也像這樣擺一擺。先在第一行擺出1個4，再在第二行擺出這樣的兩份。

生動手操作。師巡視指導學生擺小棒。

師：同學們的動手能力真強。你們看，把實心小棒看作一份，空心小棒有這樣的幾份？

生：2份。

師：每一份都是幾根？

生：4根。

師：這樣的2份也可以說是幾個幾？

生：2個4。

師：喜羊羊想在這接著擺一份小棒，請同學們快速地擺一擺，看誰擺得又對又快。

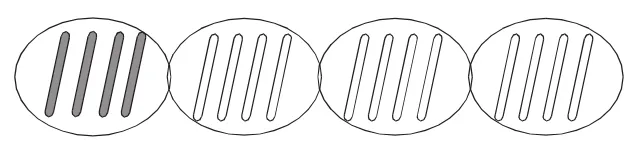
引導說：把實心小棒看作一份，空心小棒有這樣的3份，就是3個4。我們就說，空心小棒的根數是實心小棒的3倍。（板書）

師：大家都知道喜羊羊的性子可急了，只見它收走了一份。現在同學們還能不能用到剛認識的“倍”來說一說。

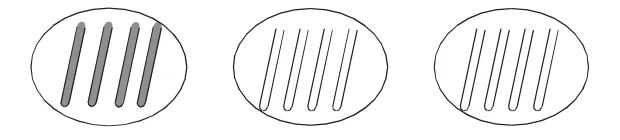
生：空心小棒的根數是實心小棒的2倍。

師：喜羊羊再收走了一份。你們還能說一說嗎？

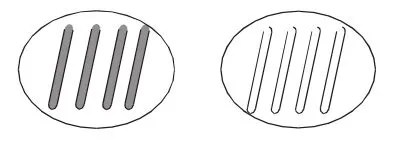
生：空心小棒的根數是實心小棒的1倍。

師：同學們再想想，如果依然把實心小棒看作一份，空心小棒有這樣的9份，我們可以說？空心小棒的根數是實心小棒的9倍。

總結：通過剛才的擺小棒我們發現，如果把實心小棒的根數看做一份，空心小棒有這樣的幾份，我們就說空心小棒的根數是實心小棒的幾倍。

從“根數”到“份數”，再到“倍數”，通過擺一擺、圈一圈、說一說，凸顯了“倍”的概念本質，幫助學生初步理解了“倍”的概念。這樣在教學中運用“數形結合”，把抽象的數學概念直觀化，讓學生經歷知識的形成過程，觸及到概念的本質。

二、數形結合——化繁為簡，理解數量關系

小學生的思維處于具體形象思維階段，但許多問題解決的數量關系通常需要抽象思維來理解。因此，這就需要教師通過“數形結合”，用形象化的圖形表達抽象化的數量關系，為學生在實際問題與算式之間、在分析數量關系與解決問題之間架設一座“橋”。

如：一袋糖平均分給三個人，如果每人吃掉6粒，那么三人剩下的糖數之和恰好是這袋糖的原來這袋糖有多少粒？用線段圖表示數量關系：

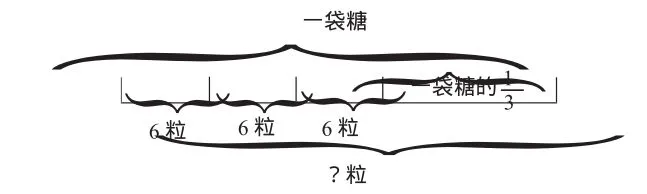
從以上解題過程可以看出，線段圖可以幫助學生理解數量關系。對于某些題，如果線段圖不能清晰地顯示其數量關系，則可以設計出其他圖形，使解題過程變得簡捷。

如：小明家買了一桶純凈水，連桶共重15千克，喝了一半水后，連桶重8千克。喝掉了多少千克水？原來滿桶的水重多少千克？

分析：桶和水之間到底是一種什么樣的數量關系？喝了一半水后，桶和水之間又是一種什么樣的數量關系？學生對此類數量關系一般感到十分抽象，不容易理解。如果教師運用下面圖形來表示，學生就會一目了然。

空桶水

沒喝前：○+■＝15千克

喝一半后：○+＝8千克

從圖中可知，喝掉的一半水后，輕了7千克，也就是說一半水是7千克，原來滿桶的水是7×2＝14（千克）。

可見，滲透數形結合思想，巧妙運用恰當的圖形來表示應用題中的數量關系，會使繁雜的數量關系簡單化，變“看不見”為“看得見”，能很好地幫助學生理清數量間的關系，提高學生分析問題、解決問題的能力，起到事半功倍的效果。

三、數形結合——從難到易，化解學習難點

學生不能化解難點主要是因為不能實現抽象的內容具體化、形象化、直觀化，數形結合能夠化抽象為具體、化復雜為簡單、變生疏為熟悉、變深奧為淺顯。

例如，在學習“異分母分數加減法”時，有些學生不理解為什么要先通分才能相加減，這時，我們可以利用“直觀模型”幫助學生理解。

環節一：

師：淘氣和笑笑分餅干，（借助多媒體課件動態演示）藍色部分表示淘氣分到的，紅色部分表示笑笑分到的，他們都知道自己分到了這塊餅干的多少，但不知道他們兩個一共分到這塊餅干的多少？請大家幫他們想想辦法好嗎？

師：算式列對了，到底一共分到這塊餅干的多少呢？咱們趕緊想想辦法吧。

師：怎樣化成分母相同的分數呢？

生：通分。

（課件演示）如果我們把這塊餅干平均分成了4份，我們就能清楚地看到淘氣分了，笑笑分到了，所以他們一共分了

師：大家會利用通分的方法算一算嗎？學生列式計算，指名匯報交流。

環節二：

環節三：

師：仔細觀察這三題，想一想，發現了什么？（教師邊播放課件邊講解）

學生通過觀看動態的課件演示，從

“形”的角度體會三道題的共性。課件出示：

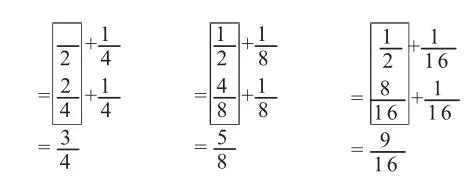
討論二：為什么要把異分母分數轉化成同分母分數？（這些算式中都有一個加數是，另一個加數各不相同，轉化后的結果也不相同，學生在“變”與“不變”的對比中，發現異分母分數加法的共性。）

上述的教學過程把抽象的分數與形象的圖形有機結合起來，學生體會到只有平均分得到的份數相同，也就是分數單位相同，分子才能相加減的道理。學生直觀地理解“通分”的必要性及異分母分數加減法的算理，同時抽象能力和抽象水平不斷提高，促進思維的發展，輕松地化解了教學難點。

總之，在小學數學教學中，數形結合的思想滲透在數學教學的每一個領域，如果說數學是知識海洋中的一艘船，那么數就是舵，形就是船上的帆，掌好“數”的舵，揚起“形”的帆，數形結合開啟思維的航船，才能駛向知識的海洋。