數控機床全生命周期重要性測度分析

谷東偉　王志瓊　趙希祿　樊少華

1.長春工業大學，長春，130012　　2.吉林大學，長春，1300253.埼玉工業大學，日本，埼玉

?

數控機床全生命周期重要性測度分析

谷東偉1王志瓊2趙希祿3樊少華2

1.長春工業大學，長春，1300122.吉林大學，長春，1300253.埼玉工業大學，日本，埼玉

引入可靠性重要性測度進行探索分析，通過分段威布爾模型確定機床早期故障期和偶然故障期的分界點，在此基礎上建立各子系統可靠性動態重要性測度模型；對早期故障期和偶然故障期子系統及整機的故障次數和故障停時進行統計分析，獲得子系統失效臨界重要性測度和子系統運行臨界重要性測度；基于時間變化的觀點對比分析三種重要性測度在早期故障期和偶然故障期確定關鍵子系統的差別，闡明單獨采用失效臨界重要性測度(故障次數)分析確定關鍵子系統的片面性。數控機床關鍵子系統的確定可為設計人員有針對性地采取糾正措施以提高數控機床可靠性和維修人員制定維修策略提供依據。

數控機床；失效臨界重要性測度；運行臨界重要性測度；全生命周期；可靠性動態重要性測度

0　引言

數控機床由多個子系統組成，不同的子系統對系統性能的影響也不盡相同[1]。在可靠性領域中，重要性測度用以評估單個零件或部件的相對重要性，通常認為零部件的相對排序比重要性測度絕對值更重要。

一個元件在一個系統中具有它的位置和可靠性，針對此問題，Birnbaum[2]1969年提出了“重要性測度”的概念，通過這個指標可以確定哪些子系統是引起系統故障的關鍵因素，確定系統可靠性改進的目標[3]。根據重要性測度所需要的知識，Birnbaum將其分為三類：結構重要性測度、可靠性重要性測度和壽命重要性測度。可靠性重要性測度又可以分為Birnbaum子系統重要性測度 (Birnbaum component importance)[4-6]、可靠性臨界重要度 (reliability criticality importance)[7-9]和運行臨界重要度(operational criticality importance)[10-11]。一般說來，可靠性重要性測度是系統運行時間的函數、系統中所有子系統故障和維修時間的函數，以及系統結構的函數。如果某個子系統對整個系統可靠性的影響程度越大，則其在整個系統中的重要度越高。

以往針對數控機床關鍵子系統的確定方法主要有FMECA(failure mode, effects and criticality analysis)[12-13]、子系統的復雜程度分析[14]和影響因素分析[15]等方法。以上幾種方法主要以每個子系統故障發生頻次為依據。然而子系統的重要度不能單純根據故障發生的頻次來計算，比如有些子系統即使頻繁發生故障，但其對整個系統的干擾程度卻微乎其微，易于維修；相反，另外一些子系統雖然極少發生故障，然而它一旦發生故障將會對整個系統帶來致命的影響，導致維修故障周期過長，嚴重影響生產的運行。

數控機床的可靠性是隨時間變化的，每個子系統的重要性也會隨時間改變，因此需要考慮子系統可靠性重要性的影響。本文克服了傳統尋找數控機床重要子系統單純考慮故障次數的靜態問題，通過引入數控機床可靠性動態重要性測度模型，分析不同時刻的子系統相對系統的重要程度，綜合分析故障次數、故障停時和可靠性確定數控機床關鍵子系統，準確量化其對數控機床可靠度影響貢獻的差異性，衡量其改進潛力，為數控機床結構可靠性設計、工藝可靠性設計、可靠性分配和可靠性增長技術的開發提供基礎數據和理論依據。

1　重要性測度模型

1.1運行臨界重要性測度模型

數控機床子系統的重要性受故障次數(failure number)和故障停時(failure down time)的影響，需要針對故障次數和故障停時分別進行基于失效的臨界重要性測度IFCI(i,t)和基于運行的臨界重要性測度IOCI(i,t)分析，其表達式如下：

(1)

(2)

式中，ni、nz分別為子系統和整機在[0， t]內所產生的故障次數;Ti、Tz分別為子系統和整機在[0， t]內所產生的總故障停機時間。

1.2子系統可靠性動態重要性測度模型

系統可靠性取決于其組成子系統的可靠性，子系統可靠性變化時,系統可靠性會隨之變化，在很多應用場合需要定量分析各子系統對系統可靠性的影響。可靠度函數是建立在故障間隔時間基礎上、能夠反映不同時刻可靠度水平的函數，故本文用可靠度函數描述子系統的可靠性動態重要性測度。數控機床從出廠使用開始會經歷三個階段：早期故障期、偶然故障期和耗損期。偶然故障期是設備使用的最佳階段，耗損期設備趨于淘汰，而早期故障期是到達偶然故障期所必須經歷的階段。本文探索通過分段威布爾模型確定機床的早期故障期和偶然故障期的分界點，分析不同運行階段的關鍵子系統。

數控機床子系統重要性測度是一個隨時間變化的量，這與系統運行狀態是相吻合的，隨著時間的發展，原來相對不重要的子系統可能變成重要的子系統，一個子系統i對系統φ正常的可靠性動態重要性測度表示為

IBs(i,p)=Pr{φ(X)=1|Xi=1}-Pr{φ(X)=1}

式中，p為路集；φ(X)為系統結構函數；Xi=1表示元件i正常，Xi=0表示元件i失效；Pr(·)為概率函數。

對于一個由獨立元件組成的關聯系統則有

IBs(i,p)=Pr{φ(X)=1|Xi=1}-Pr{φ(X)=1}

IBs(i,p)=qiE{[φ(X)=1|Xi=1]-

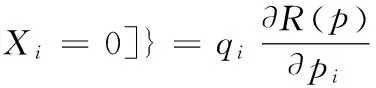
式中，qi為元件或子系統i的可靠度值； pi為含元件i的路集；R(p)為路集可靠度函數；E為數學期望。

根據上式可知，IBs(i,p)通過子系統i的可靠性對系統可靠性的增長速率來衡量子系統i對系統可靠性的重要性測度，即

(3)

式中,IBs(i,p)為子系統i的可靠性動態重要性測度;Rsys為系統可靠度函數；Ri為子系統可靠度函數。

由于可靠性重要性測度表示的是系統可靠度對子系統可靠度的變化率，故式(3)的物理意義為：對于系統中任意兩個子系統的可靠性重要性測度IBs(i,p)與IBs(j,p)，若IBs(i,p)>IBs(j,p)，則說明提高子系統i的可靠性水平對系統可靠性水平提高的貢獻更大，從而間接表明子系統i比j更重要，即IBs(i,p)越大，部件i可靠度的變化引起系統可靠度的變化越大。因此，改進可靠性影響度較大的子系統并提高其可靠度，可使系統的可靠度有較大的改善。

2　實例計算

根據某型號數控機床的現場故障數據分別計算整機和子系統的可靠度函數，本文對液壓系統(D)、橫梁(B)、伺服系統(F)、潤滑系統(L)、刀架(M)、CNC系統(NC)、主傳動系統(S)、工作臺(T)和電氣系統(V)等9個子系統進行可靠性重要性測度分析。

由于該批故障數據在采集時從機床出廠交付用戶使用即開始記錄(不含調試期)，所采集的數據包括故障早期故障期和偶然故障期的數據，所以對獲得故障時刻數據采用兩階段威布爾分布描述更為合理。分布函數的第一階段可以理解為數控機床早期故障期的分布模型，第二階段可以理解為數控機床偶然故障期的分布模型[15]。分別考慮早期故障期和偶然故障期機床各子系統對整機的重要程度。分段威布爾模型的可靠性函數為

(4)

通過對故障數據的模型初選、數據擬合以及假設檢驗，得到該型號數控車床的兩階段威布爾分布模型為

Rsys(t)=

(5)

根據上面的分析可知，在0～706h內為此機床的早期故障期，在706h開始為偶然故障期。通過數據擬合，假設檢驗得到各子系統的可靠度函數如表1所示。

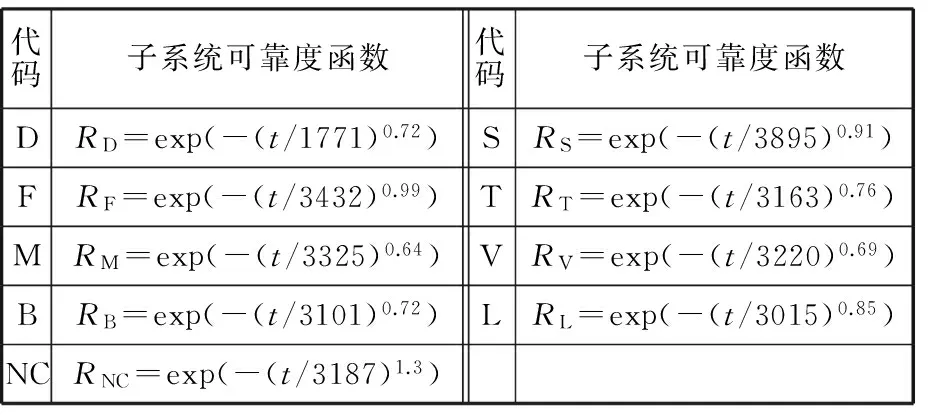
表1　子系統可靠度函數匯總表

2.1子系統可靠性動態重要性測度模型

數控車床各子系統在早期故障期和偶然故障期的故障次數及故障停時數據如表2所示，例如，伺服系統在早期故障期故障次數10次，故障停時122 h，其故障主要表現為伺服電機風機損壞、驅動器報警、伺服電機軸齒輪損壞、編碼器硬件故障等；偶然故障期故障次數28次，故障停時322 h，故障主要表現為主軸編碼器損壞、光柵尺故障等。

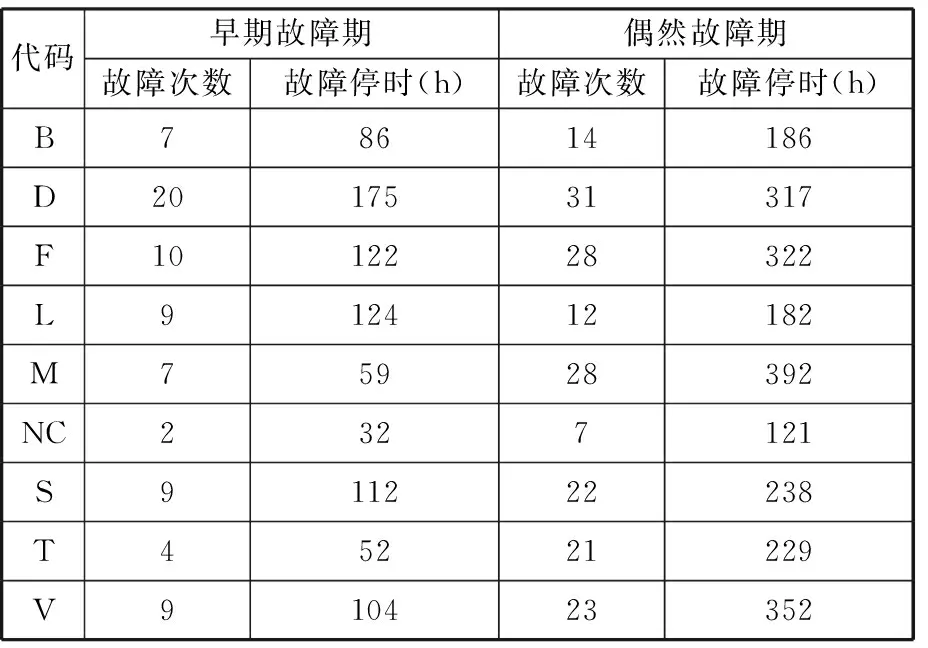
表2　子系統故障次數和故障停時匯總表

根據表1中故障次數和故障停機時間進行早期故障期和偶然故障期失效臨界重要性測度IFCI(i,t)和運行臨界重要性測度IOCI(i,t)分析，如表3所示。

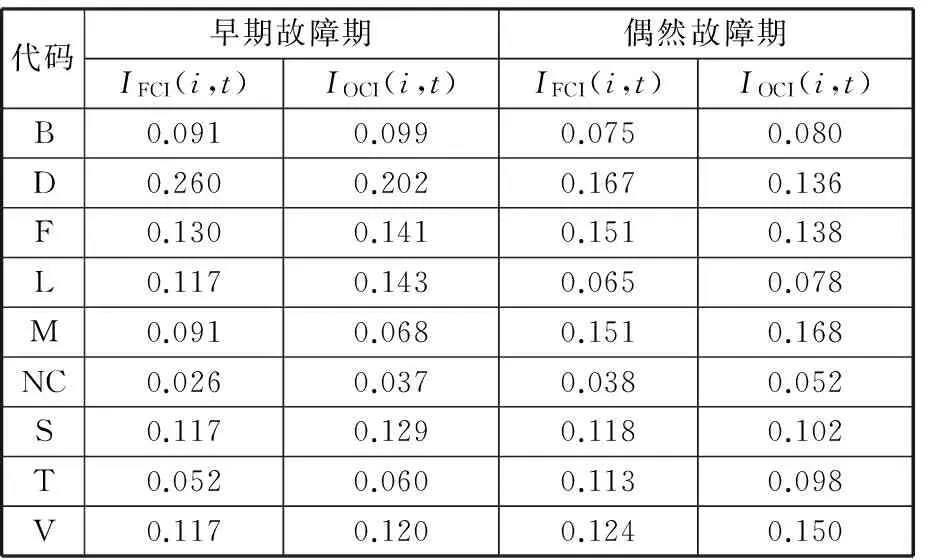
表3　子系統失效和運行臨界重要性測度表

2.2子系統可靠性動態重要性模型

根據式(4)、式(5)，得到各子系統在早期故障期和偶然故障期的可靠性重要性測度模型為

(6)

以液壓系統(D)為例，由式(6)以及液壓系統(D)的可靠度函數可得液壓系統(D)在早期故障期和偶然故障期的可靠性重要性測度模型分別為

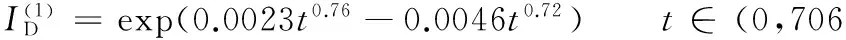
t∈(706 h,∞)

同樣可以計算各子系統在早期故障期和偶然故障期可靠性重要性測度模型。

3　分析

通過MATLAB軟件畫出各子系統可靠性重要性測度函數曲線見圖1。

由圖1可知，不同時刻各子系統對整機的可靠性重要程度是不同的，而各子系統的可靠性動態重要性測度排序在某一時間段也存在差異。計算9個子系統在600 h和5000 h的可靠性動態重要性測度值，并進行歸一化，得到各子系統重要度在早期故障期和偶然故障期的排序結果如表4和表5所示。

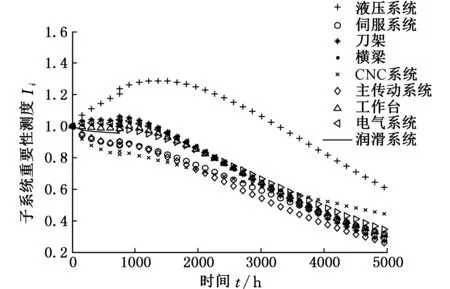
圖1　子系統可靠性動態重要性測度曲線圖

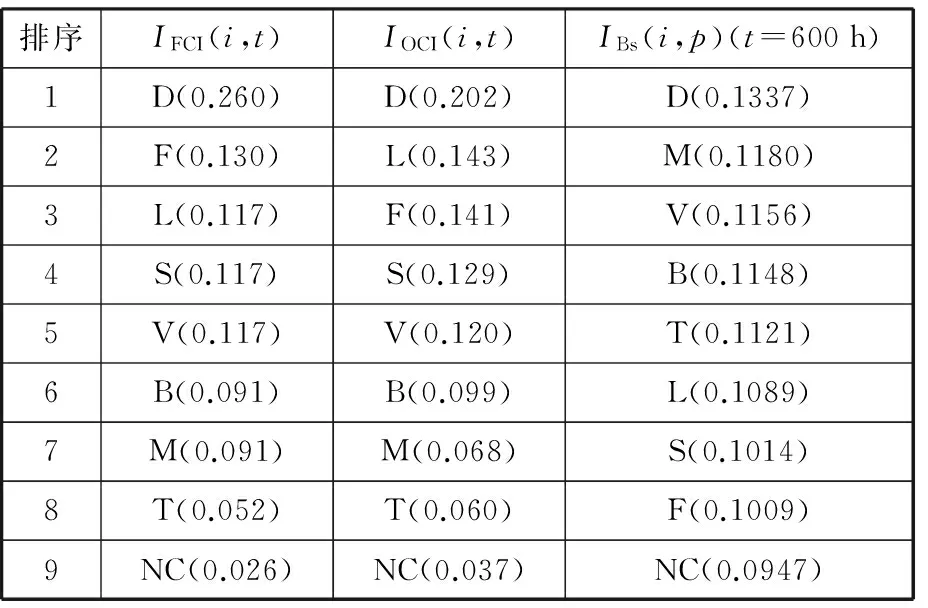
排序IFCI(i,t)IOCI(i,t)IBs(i,p)(t=600h)1D(0.260)D(0.202)D(0.1337)2F(0.130)L(0.143)M(0.1180)3L(0.117)F(0.141)V(0.1156)4S(0.117)S(0.129)B(0.1148)5V(0.117)V(0.120)T(0.1121)6B(0.091)B(0.099)L(0.1089)7M(0.091)M(0.068)S(0.1014)8T(0.052)T(0.060)F(0.1009)9NC(0.026)NC(0.037)NC(0.0947)

表5　偶然故障期子系統重要度值排序表

根據表4和表5可得到各子系統在早期故障期和偶然故障期各重要性測度排序類比圖，見圖2、圖3。

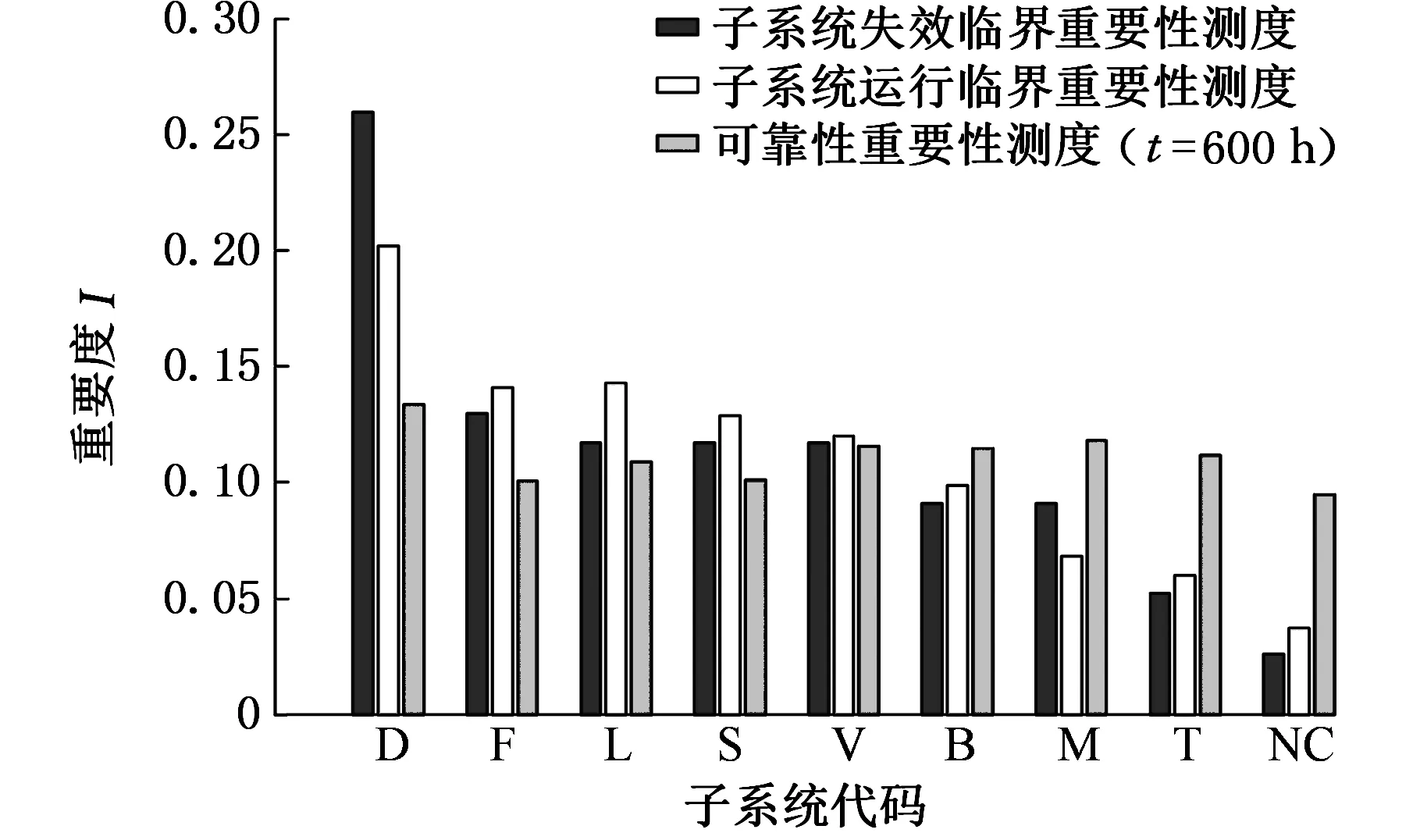
圖2　早期故障期子系統重要性測度排序類比圖

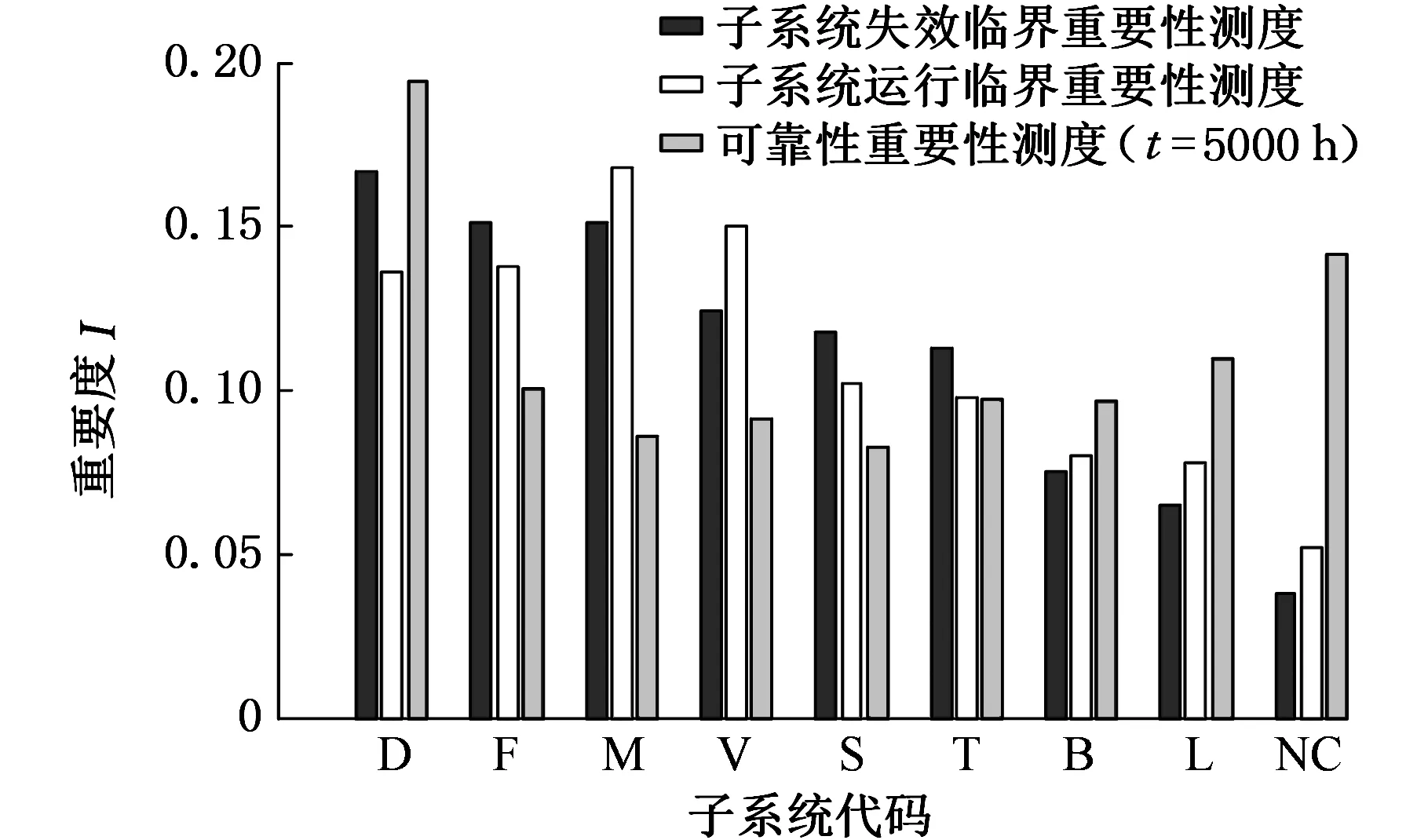
圖3　偶然故障期子系統重要性測度排序類比圖

分析表4和圖2可知，在早期故障期，液壓系統(D)的三個可靠性重要性測度指標均排名第一位；伺服系統(F)和潤滑系統(L)雖然可靠性動態重要性測度較靠后，但其失效臨界重要性測度和運行臨界重要性測度排名均為第二和第三，對整機的可靠性影響不容忽略；雖然電氣系統(V)沒有一個可靠性影響度指標排名明顯居前，但綜合考慮三個指標，可以認為其對整機的可靠性影響也較大。刀架雖然失效臨界重要性測度和運行臨界重要性測度指標排名靠后，但其可靠性動態重要性測度排名為第二，以上的分析說明故障次數的多少并不能完全解釋子系統故障對整機的影響程度。因此在早期故障期液壓系統(D)、電氣系統(V)、伺服系統(F)和潤滑系統(L)為整機的關鍵子系統。

根據表5和圖3可知，在偶然故障期，對整機可靠性影響最大的三個關鍵子系統是液壓系統(D)、伺服系統(F)和刀架(M)。相對于早期故障期而言，液壓系統(D)的運行臨界重要性測度較早期故障期的排名降低；而伺服系統(F)和工作臺(T)的三個影響度指標則有明顯的上升趨勢，說明隨著時間的推移，各子系統對整機的重要度必然發生變化。

4　結論

(1)無論在早期故障期還是偶然故障期，液壓系統(D)都是關鍵子系統，要提高此系列數控車床的可靠性，首先要從液壓系統進行可靠性設計改進。

(2)不能完全依據故障次數即失效臨界重要性測度的排序來確定機床各子系統對整機可靠性的影響。

(3)通過子系統三個不同的重要性測度指標的排序，綜合考慮了各子系統對整機的重要程度，尤其對于可靠性動態重要性測度的引入，實現了實時動態管理。可以根據各子系統的重要性測度排序變化，制定相應的維修計劃。

(4)早期故障期和偶然故障期各子系統對整機的影響存在明顯的差別，可靠性動態重要性測度的變化尤為明顯。為提高整機的可靠度，應該根據不同時期子系統重要性測度排名制定相應的改進措施，為系統有效地提高機床的可靠性提供依據。

[1]楊兆軍,陳傳海,陳菲,等.數控機床可靠性技術的研究進展[J].機械工程學報,2013,49(20):130-139.

YangZhaojun,ChenChuanhai,ChenFei,etal.ProgressintheResearchofReliabilityTechnologyofMachineTools[J].JournalofMechanicalEngineering, 2013,49(20): 130-139.

[2]BirnbaumZW.OntheImportanceofDifferentComponentsinaMulti-componentSystem[M].NewYork：AcademicPress, 1969.

[3]郭位, 朱曉巖.系統重要性測度原理與應用[M].北京：國防工業出版社，2014.

[4]EryilmazS,BozbulutAR.ComputingMarginalandJointBirnbaum,andBarlow-proschanImportancesinWeighted-k-out-of-n:GSystems[J].Computers&IndustrialEngineering, 2014, 72: 255-260.

[5]ContiniS,MatuzasV.NewMethodstoDeterminetheImportanceMeasuresofInitiatingandEnablingEventsinFaultTreeAnalysis[J].ReliabilityEngineeringandSystemSafety, 2011, 96(7):775-784.

[6]YadavOP,XingZhuang.APracticalReliabilityAllocationMethodConsideringModifiedCriticalityFactors[J].ReliabilityEngineering&SystemSafety, 2014, 129: 57-65.

[7]FreixasJ,PonsM.TheInfluenceoftheNodeCriticalityRelationonSomeMeasuresofComponentImportance[J].OperationsResearchLetters,2008,36(5): 557-560.

[8]AndrewsJD.BirnbaumandCriticalityMeasuresofComponentContributiontotheFailureofPhasedMissionsOriginalResearchArticle[J].ReliabilityEngineering&SystemSafety, 2008, 93(12):1861-1866.

[9]VaurioJK.ImportanceMeasuresforMulti-phaseMissions[J].ReliabilityEngineering&SystemSafety, 2011, 96(1): 230-235.

[10]SiShubin,LevitinG,DuiHongyan,etal.ImportanceAnalysisforReconfigurableSystems[J].ReliabilityEngineering&SystemSafety, 2014,126:72-80.

[11]WangYuanhang,DengChao,WuJun,etal.ACorrectiveMaintenanceSchemeforEngineeringEquipment[J].EngineeringFailureAnalysis, 2014,36: 269-283.

[12]KimKO,YangYoonjung,ZuoMJ.ANewReliabilityAllocationWeightforReducingtheOccurrenceofSevereFailureEffects[J].ReliabilityEngineering&SystemSafety, 2013,117: 81-88.

[13]陳炳錕,申桂香,張英芝,等.隨機模糊理論下的數控機床動態危害性[J].吉林大學學報(工學版),2010,40(增刊1)：262-265.

ChenBingkun,ShenGuixiang,ZhangYingzhi,etal.DynamicalCriticalityAnalysisofCNCMachineToolBasedonRandomFuzzyTheory[J].JournalofJilinUniversity(EngineeringandTechnologyEdition), 2010,40(S1)：262-265.

[14]WangYiqiang,JiaYazhou,YuJunyi.FailureProbabilisticModelofCNCLathes[J].ReliabilityEngineeringandSystemSafety,1999,65:307-314.

[15]高萍,吳甦,賈希勝.復雜系統的可靠性模型及參數估計方法[J].系統仿真學報,2009, 21(13):4140-4148.

GaoPing,WuSu,JiaXisheng.ReliabilityModelofComplexSystemandItsParametersEstimationMethod[J].JournalofSystemSimulation, 2009, 21(13):4140-4148.

(編輯蘇衛國)

Importance Measures Analyses of CNC Machine in Total Life Cycle

Gu Dongwei1Wang Zhiqiong2Zhao Xilu3Fan Shaohua2

1.Changchun University of Technology,Changchun，130012 2.Jilin University,Changchun，130025 3.Saitama University,Saitama-ken,Japan

This paper introduced reliability importance measure to exploratory analyses. The dividing points were determined through piecewise Weibull model for random failure periods and early failure periods, then the subsystem reliability importance measure dynamic model was established. The failure critical importance measure and operational critical importance measure could be obtained with the statistics of failure numbers and failure down time. Finally, the three importance measures were compared and the key subsystem was determined based on the time variation in random failure periods and early failure periods. The sidedness of ascertaining the key subsystem was elucidated with failure critical importance measure (failure number) alone. Besides, the key subsystems were found and this result will be helpful for design, failure analysis and reliability improvement.

CNC machine; failure criticality importance measure; operational criticality importance measure; total life cycle; reliability dynamic importance measure

2015-05-16

教育部“春暉計劃”資助項目(Z2014140)；吉林省科技發展計劃資助項目(20140520126JH)

TG659

10.3969/j.issn.1004-132X.2016.20.011

谷東偉，男，1983年生。長春工業大學機電工程學院講師、博士。研究方向為數控機床可靠性維修性。王志瓊(通信作者)，女，1986年生。吉林大學機械科學與工程學院工程師。趙希祿，男，1961年生。埼玉工業大學工學部教授。樊少華，男，1980年生。吉林大學機械科學與工程學院博士。