考慮摩擦的球面切向接觸剛度分形模型研究
劉 鵬 陳 奇 樊 浩 黃守武
合肥工業大學,合肥,230009
?
考慮摩擦的球面切向接觸剛度分形模型研究
劉鵬陳奇樊浩黃守武
合肥工業大學,合肥,230009
為準確且方便地計算兩球面的切向接觸剛度(TCS),在前期對兩球面接觸分形模型研究的基礎上,通過引入考慮摩擦因素的彈塑性變形臨界面積計算公式,并基于接觸面切向剛度基本理論,建立了考慮摩擦因素的兩球面切向接觸剛度的分形模型。對模型進行了仿真分析,結果表明:切向接觸剛度與法向載荷成正比關系;摩擦因數與切向接觸剛度的關系因分形維數的變化而呈現出不同的規律;受到分形維數變化的影響,切向接觸剛度隨接觸面材料特性參數和分形粗糙度幅值的增大而增大;在一定工況下,切向接觸剛度在分形維數取1.5時達到最大,且當分形維數在1.5左右時,其值增大最快;球面內接觸比外接觸時的切向剛度大;隨著曲率半徑的增大,切向剛度增大。研究結果為后續開展高副結合面(如軸承等)潤滑及動力學分析提供了理論基礎。
摩擦;球面;切向接觸剛度; 分形理論
0 引言
目前,針對結合面微觀形貌對切向接觸剛度影響的研究越來越受到重視,但研究中常常忽視了結合面的類型(平面或曲面)對切向剛度的影響,同時常常忽略了摩擦因素的影響,或者摩擦因素考慮不夠全面。
張學良等[1]最早提出了基于分形理論的切向接觸剛度計算方法;田紅亮等[2-3]基于各向異性分形幾何理論,建立了結合面切向接觸剛度改進模型,通過對所建模型的數字仿真,直觀地揭示了結合面切向接觸剛度與結合面法向載荷、切向載荷、分形維數、分形粗糙度、相關因子及材料特性之間復雜的非線性關系;李小彭等[4]研究了考慮摩擦因素的結合面切向接觸剛度分形模型,該模型雖然考慮了摩擦因素的影響,但未能區分結合面的形式(平面或曲面)。上述研究對象主要是平面結合面,未能明確界定接觸面形式對切向接觸剛度的影響,且未能全面考慮摩擦因素的影響。
趙韓等[5-7]在M-B分形模型的基礎上,提出了基于粗糙曲面的分形接觸模型,并進行了曲面切向接觸剛度的分形計算模型研究;Shi等[8]對圓柱體結合面的切向接觸剛度進行了研究。上述針對非平面接觸的切向剛度分形模型研究主要集中于圓柱體接觸問題,目前尚未見針對球面接觸面切向接觸剛度的研究報道。
因此,為了全面考慮摩擦因素對球面接觸中切向接觸剛度計算的影響,本文在研究團隊前期非平面分形接觸模型研究的基礎上,通過對球面分形接觸模型進行修正,建立了綜合考慮摩擦因素的兩球面切向接觸剛度計算的分形模型,并通過對模型進行仿真分析,獲得相關參數對切向接觸剛度的影響趨勢與規律。
1 考慮摩擦因素的兩球面切向接觸剛度分形模型
1.1結合面分形接觸模型
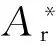
(1)
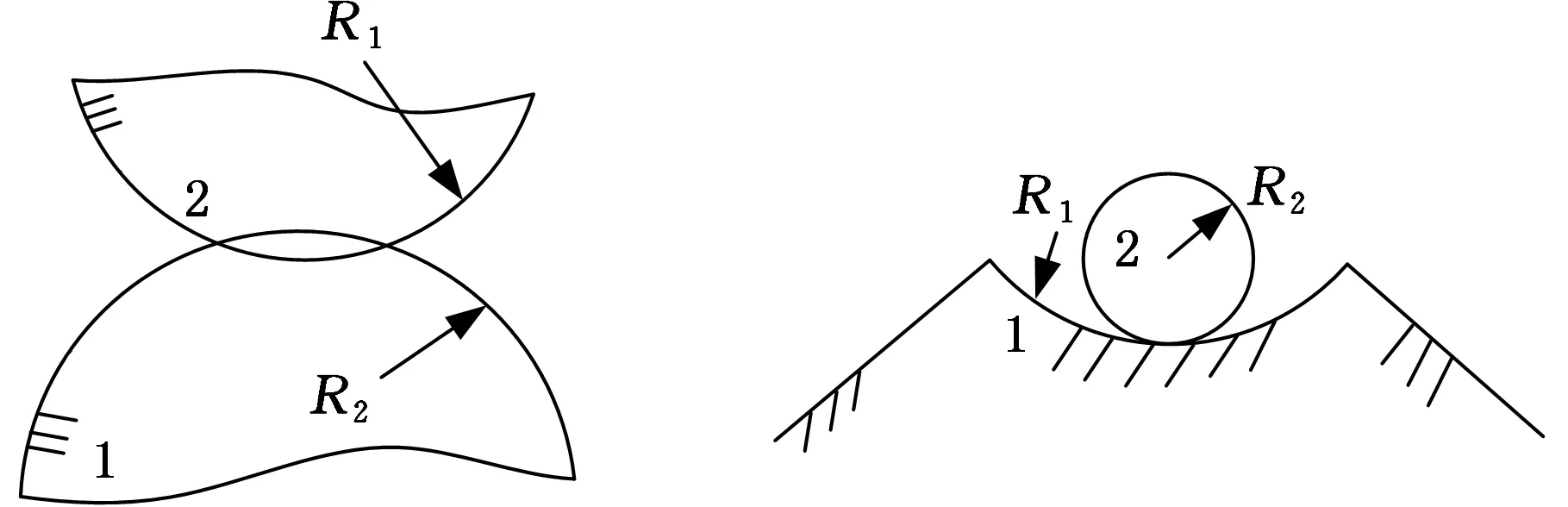
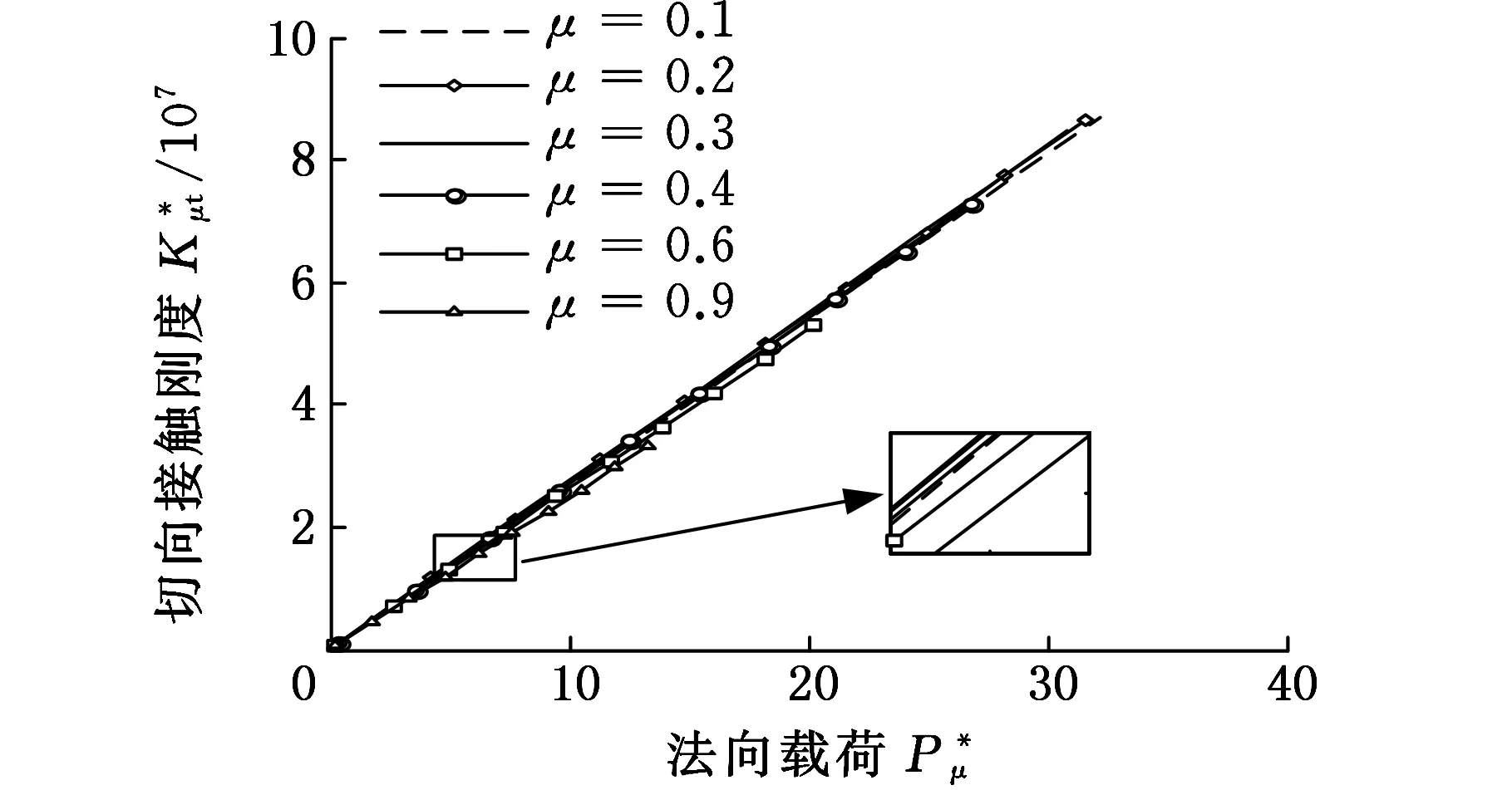
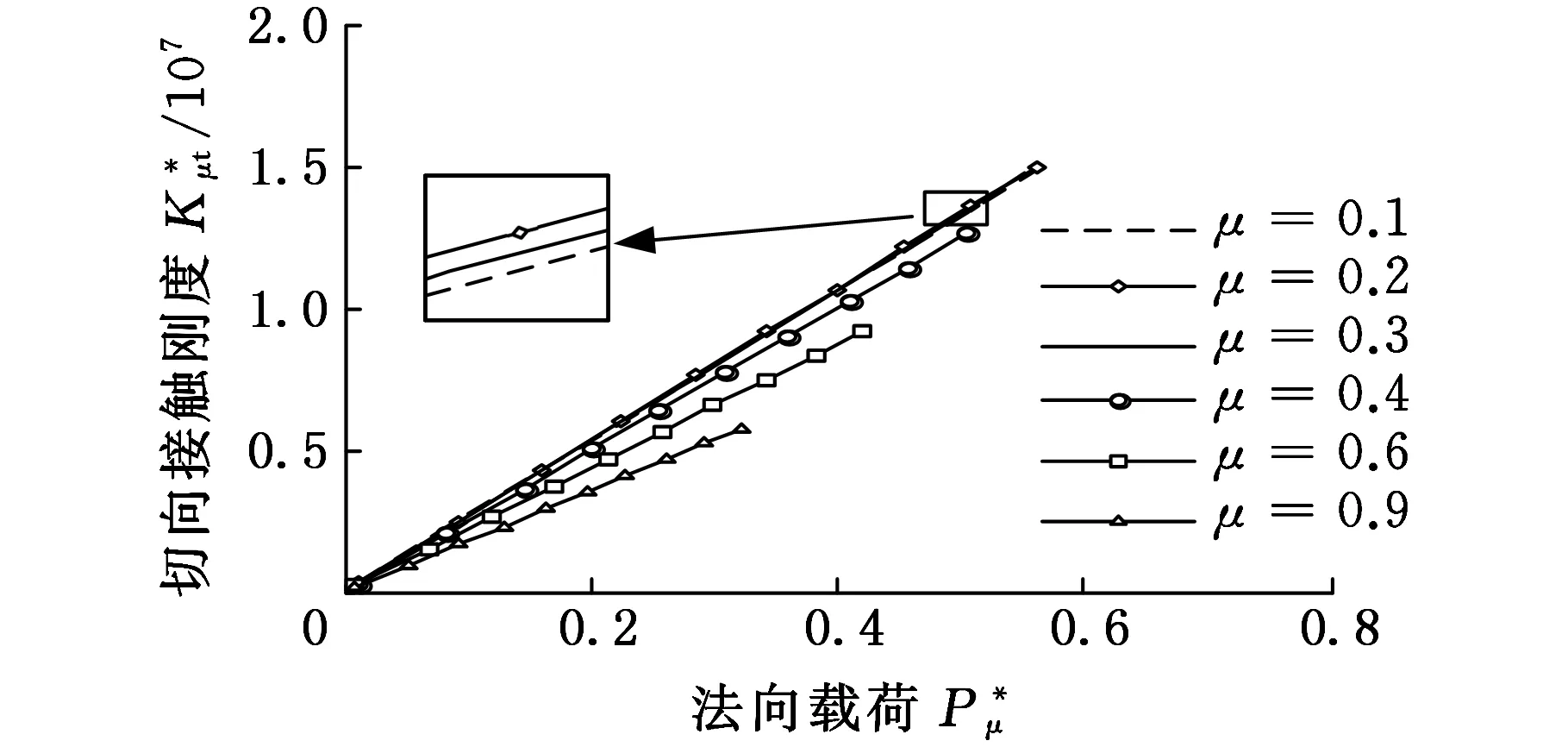
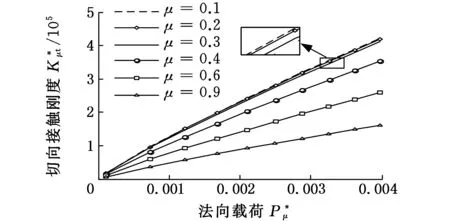
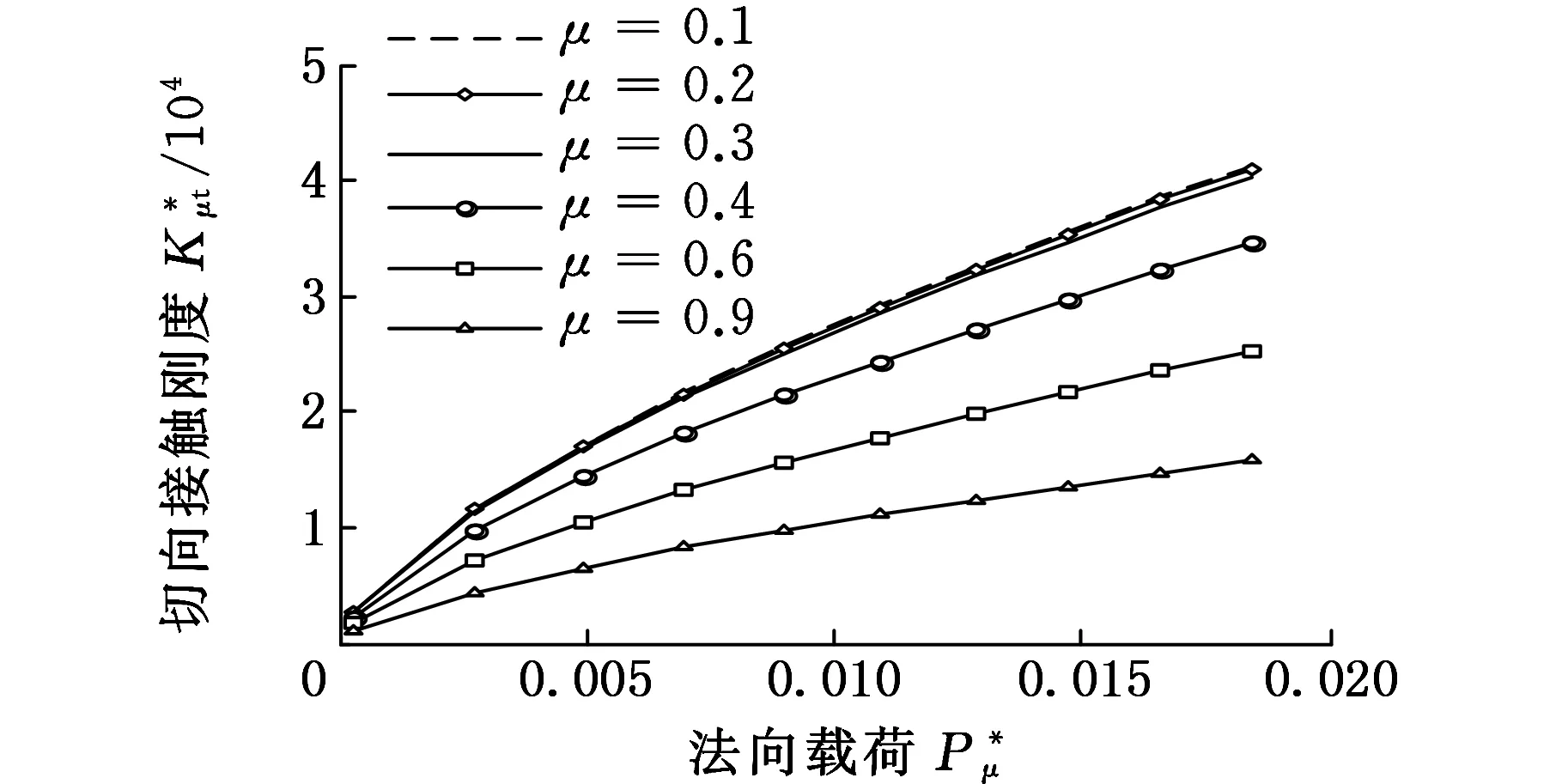
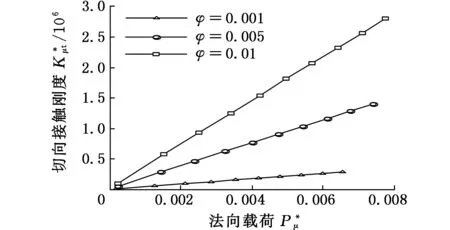
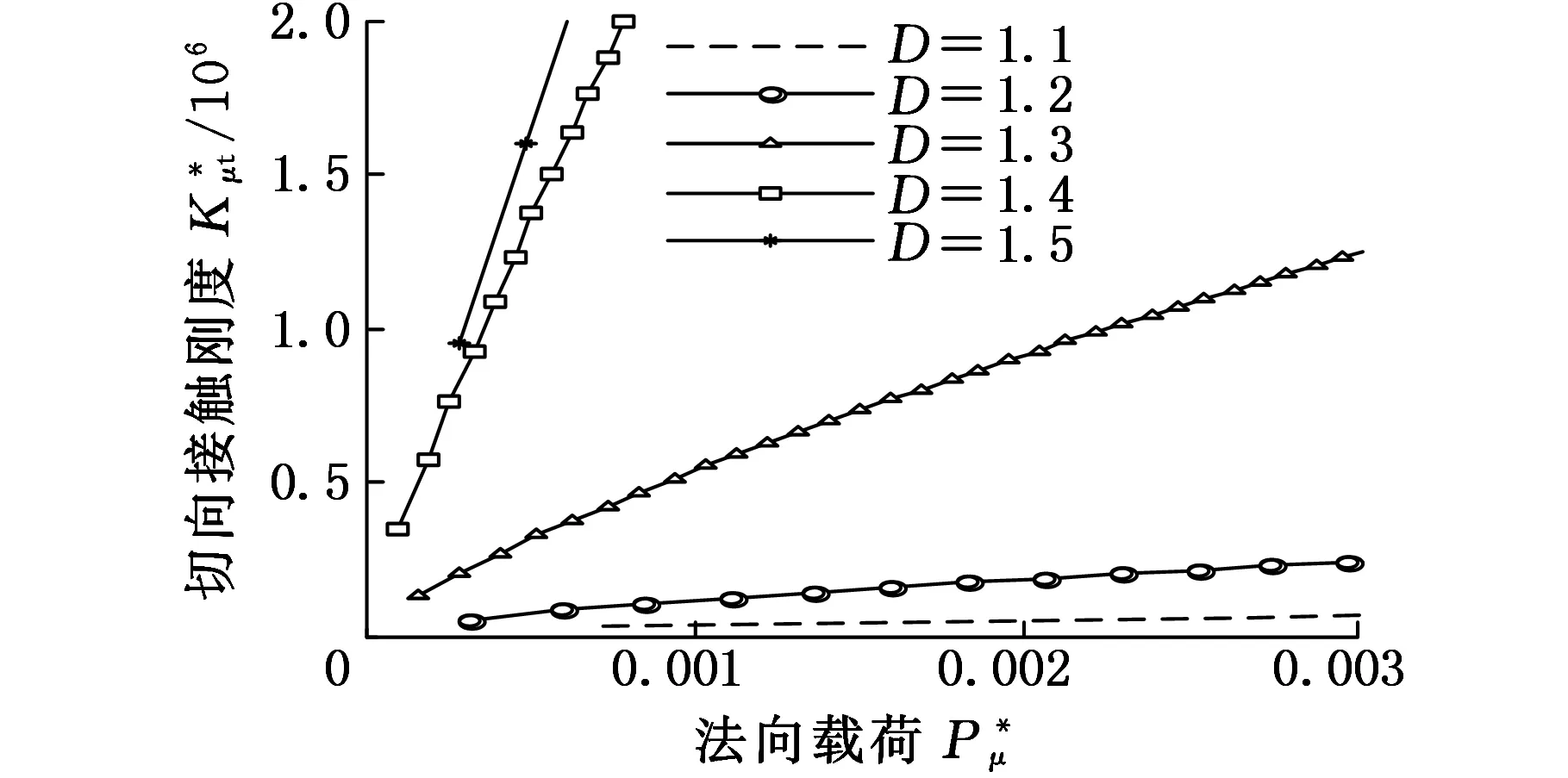
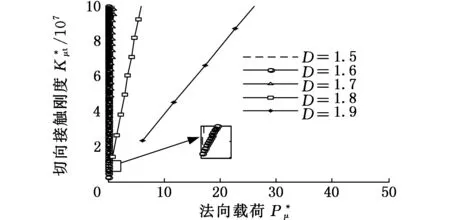
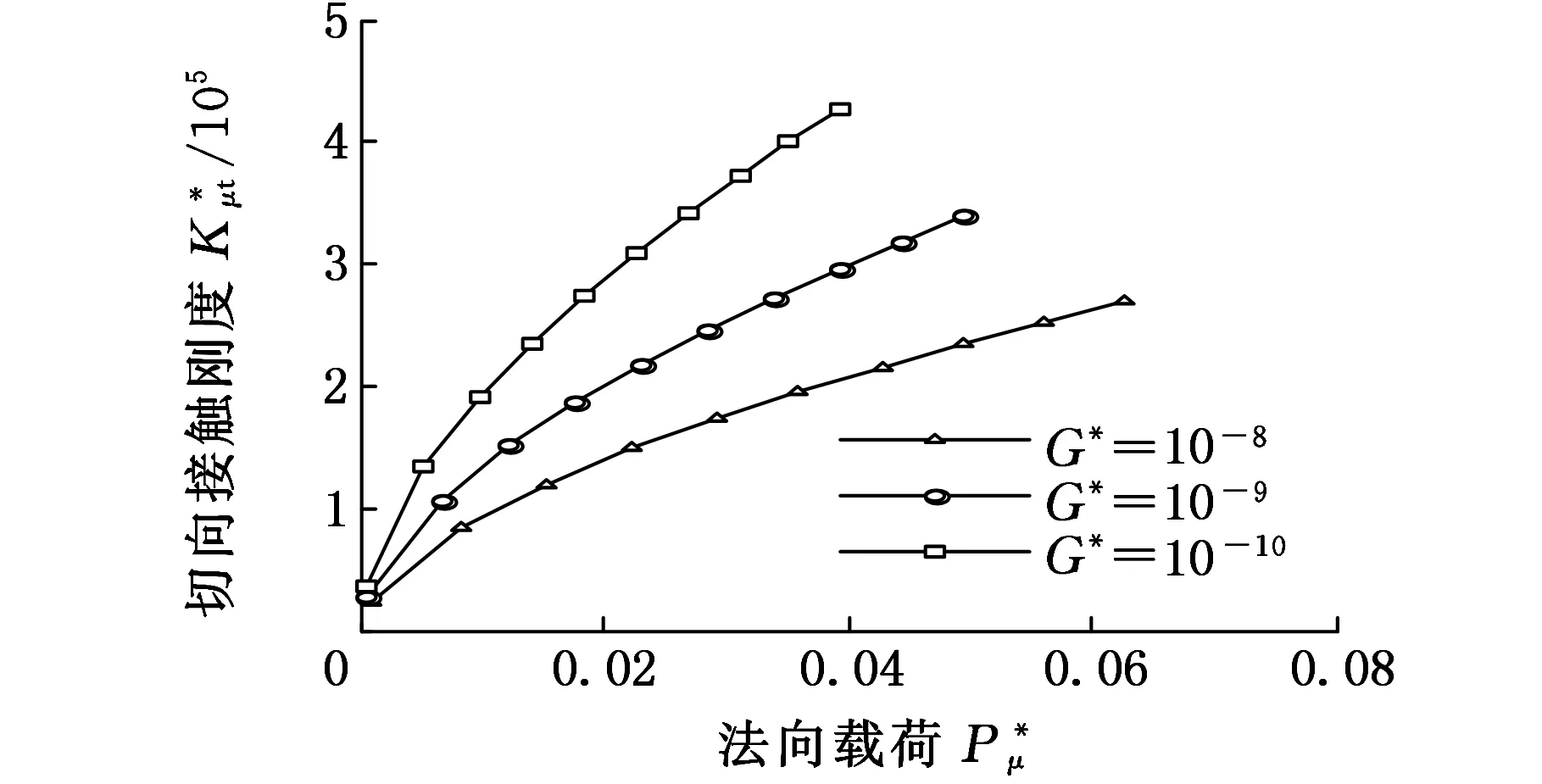
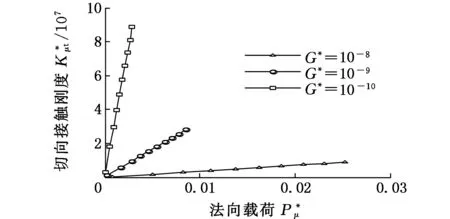
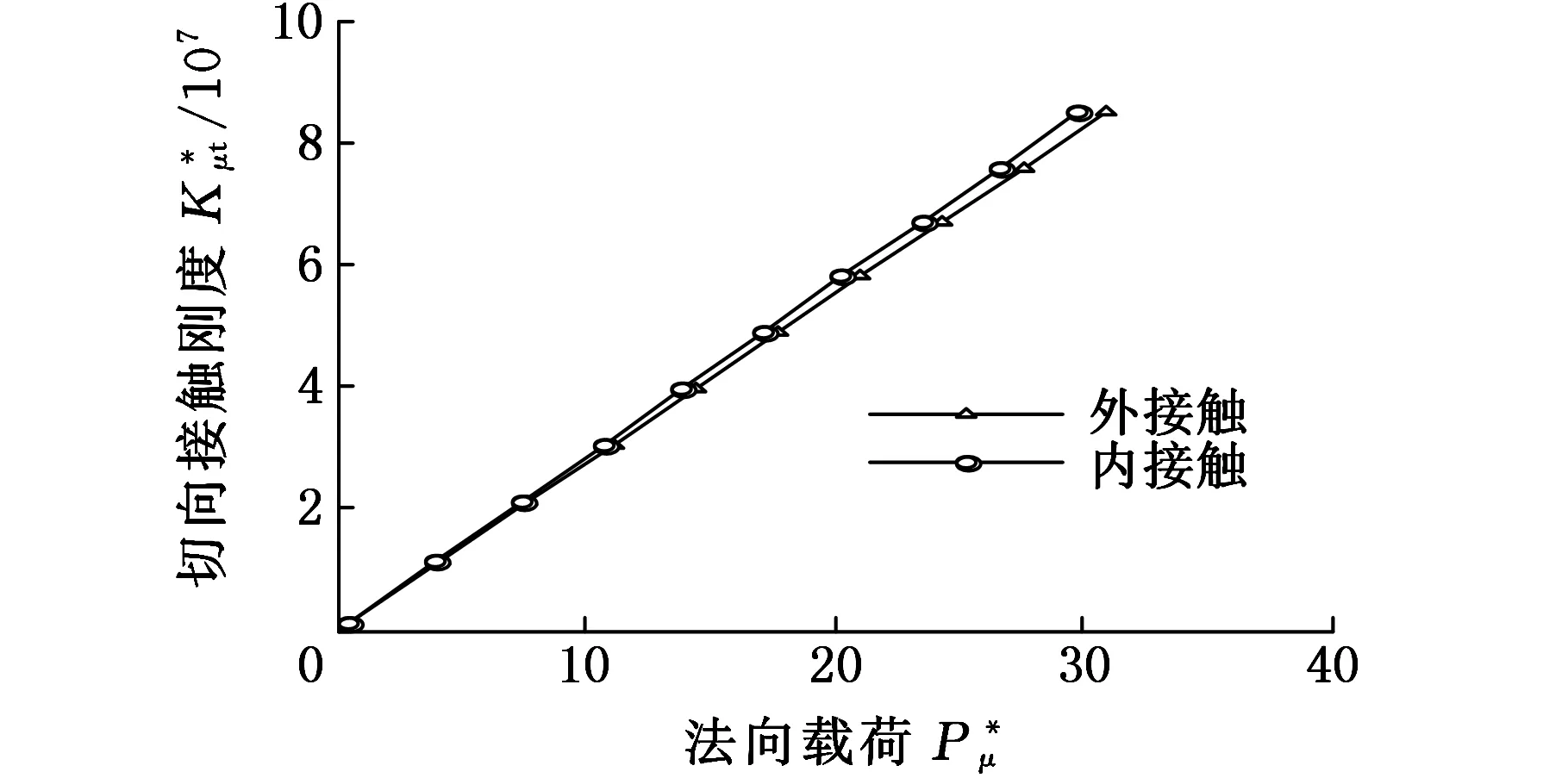
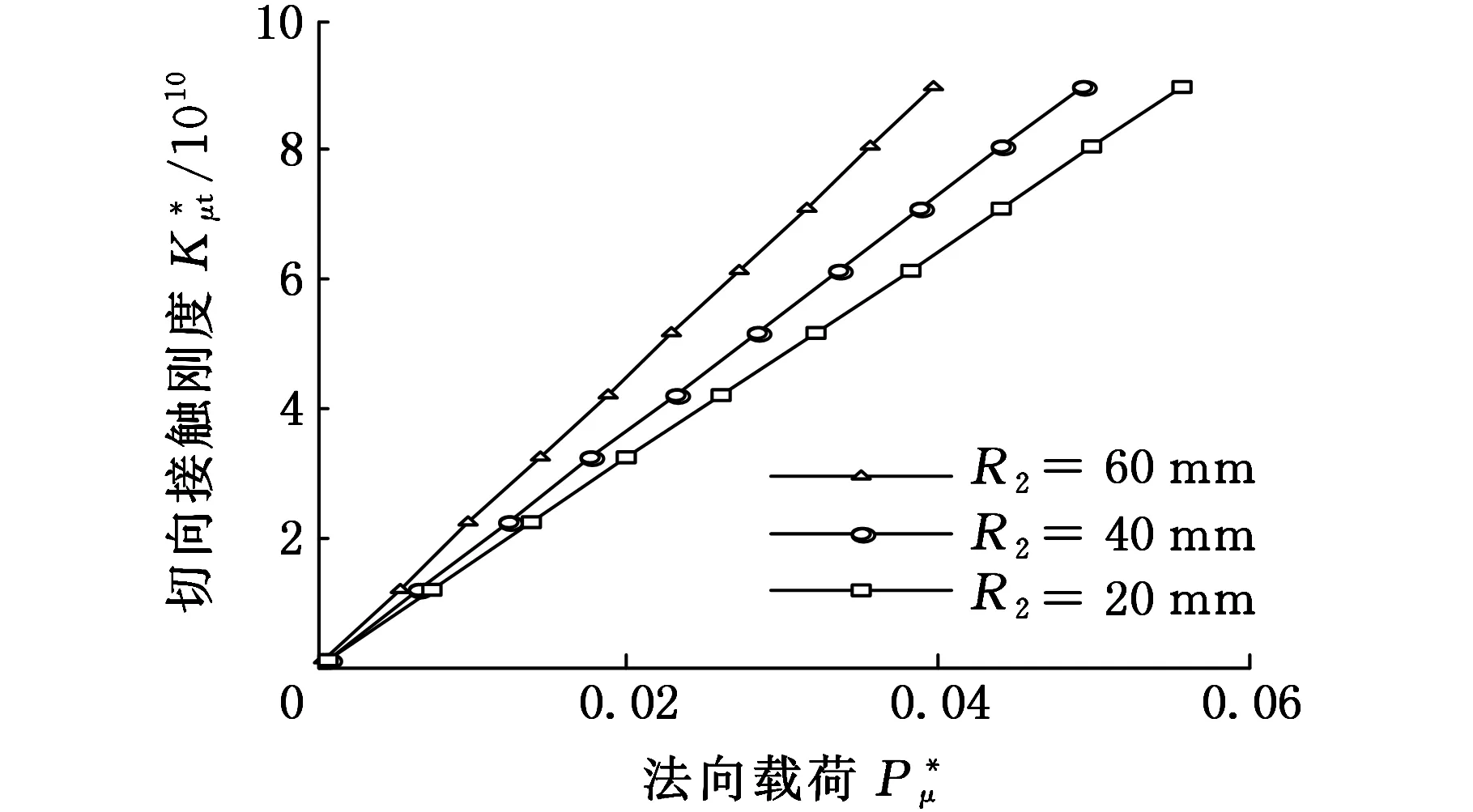
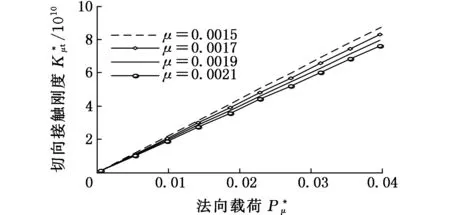
式(1)具體函數關系分為al>ac(al為最大接觸點的面積,ac為微凸體彈塑性臨界接觸面積)和al (1)當al>ac時,接觸點處于彈塑性接觸狀態,此時又分成兩種情況: a.D≠1.5(D為分形維數)時,有 (2) b.D=1.5時,有 (3) (2)當al (4) (5) 1.2結合面切向接觸剛度 根據文獻[11]可得,切向接觸剛度的基本公式為 (6) 式中,υ為材料的泊松比;h為載荷比例系數,h=T/P;T為切向載荷;P為法向載荷;μ為接觸面的摩擦因數。 1.3考慮摩擦因素的彈塑性變形臨界面積公式 根據文獻[4],摩擦對分形接觸模型的影響主要體現在彈塑性變形的臨界面積計算方面。利用考慮摩擦因素的臨界面積計算公式,并結合已有的兩球面分形接觸模型,即可建立考慮摩擦因素的球面分形接觸模型。 根據文獻[4]可得,考慮摩擦因素的彈塑性變形的臨界面積計算公式為 (7) 其中,aμc為考慮摩擦因素的彈塑性變形臨界面積(本文中,帶下標μ的物理量表示考慮摩擦因素下的物理量);kμ為摩擦力修正因子,其計算公式為 (8) 1.4考慮摩擦因素的球面彈塑性接觸載荷公式 將式(7)、式(8)代入式(2)~式(5)中,并結合兩球面的接觸面積分布公式,即可獲得考慮摩擦因素的兩球面彈塑性接觸載荷公式(即分形接觸模型),其量綱一形式如下:(1)當al>aμc時,接觸點處于彈塑性接觸狀態,此時又分成兩種情況: a.D≠1.5時,有 (9) b.D=1.5時,有 (10) (2)當al (11) (12) 其中,a為微凸體面積,球面接觸系數λC的計算公式為[11] (13) 其中,R1和R2為兩球面的曲率半徑;“±”符號中,“+”表示外接觸,“-” 表示內接觸(假設R1>R2),如圖1所示,圖中,1、2表示球面1和球面2。 (a)外接觸 (b) 內接觸圖1 球面接觸示意圖 將式(7)代入式(6)即可得到考慮摩擦因素的切向剛度基本計算式: (14) 本節對式(14)進行仿真,通過考察不同參數(如摩擦因數、分形維數、粗糙度幅值、材料的特性參數、曲率半徑)以及不同接觸形式對球面切向接觸剛度的影響,找出切向接觸剛度與這些參數之間的相互關系與變化規律。 假設兩球面副的基本參數如下:彈性模量E1= E2=206GPa,泊松比υ1=υ2=0.3,曲率半徑分別為R1=100mm,R2=60mm。 2.1摩擦因數對切向接觸剛度的影響 當其他參數固定時,切向接觸剛度與法向載荷關系以及摩擦因數對切向接觸剛度的影響情況如圖2所示。由圖2可以看出,在分形維數D=1.9的情況下,當摩擦因數μ=0.3時出現切向接觸剛度的最大值;而在分形維數為1.6~1.8的情況下,當摩擦因數μ=0.2時出現切向接觸剛度的最大值;當分形維數小于1.5之后,切向接觸剛度隨著摩擦因數的增大而減小。另外,當摩擦因數為0.1~0.3時,摩擦因數的變化對切向接觸剛度的影響較小(圖中曲線幾乎重合);當摩擦因數為0.3~0.9時,切向接觸剛度受摩擦因數影響的敏感度提高。 同時由圖2可見,當摩擦因數固定時,切向接觸剛度與法向載荷之間為正比關系,即隨著法向載荷的增大,切向接觸剛度也隨之增大。這一結論與文獻[1-2]中的實驗結果吻合,從而驗證了本文模型的正確性。 2.2材料的特性參數對切向接觸剛度的影響 由圖3可知,切向接觸剛度隨著材料特性參數的增大而增大。由材料特性參數公式φ=σy/E容易看出,φ隨σy的增大而增大,即較軟材料的屈服強度σy增大,接觸表面能夠承受的切向力增大,因此,切向接觸剛度與材料的特性參數成線性正比關系的結論是合理的。 2.3分形維數對切向接觸剛度的影響 當分形維數小于1.5時,在相同載荷情況下,切向接觸剛度隨著分形維數的增大而增大(圖4a),而在分形維數大于1.5之后,分形維數與切向接觸剛度成反比關系(圖4b),這一結論與文獻[4-6]的分析結果一致,即存在一個使接觸剛度達到極值的分形維數值。 (a)D=1.9 (b)D=1.7 (c)D=1.4 (d)D=1.2圖2 摩擦因數對切向接觸剛度的影響(G*=10-9,φ=0.005,R1=100 mm,R2=60 mm) 圖3 材料的特性參數對切向接觸剛度的影響(D=1.5,μ=0.3,G*=10-9,R1=100 mm,R2=60 mm) (a)D≤1.5 (b)D≥1.5圖4 分形維數對切向接觸剛度的影響(φ=0.1, μ=0.3, G*=10-9,R1=100 mm,R2=60 mm) 圖4中分形維數變化較大,在某些分形維數下,沒有清楚地反映曲線變化趨勢,但由圖2可以明顯看出,在分形維數大于1.4時,切向接觸剛度與法相載荷成線性正比關系,而當分形維數小于1.4之后,切向接觸剛度隨載荷增大的速率逐漸放緩。同時,由圖4可得,當分形維數在1.5左右時,切向接觸剛度受法向載荷的影響敏感度增加,即相同法向載荷變化范圍,將引起切向接觸剛度的較大變化。 2.4粗糙度幅值對切向接觸剛度的影響 (a)D=1.1 (b)D=1.5圖5 粗糙度幅值對切向接觸剛度的影響(μ=0.3,R1=100 mm,R2=60 mm) 由圖5可知,粗糙度幅值增大將使切向接觸剛度減小;此外,由于粗糙度幅值與分形維數共同決定接觸表面的微觀形貌,因此不同分形維數與粗糙度幅值的組合對切向接觸剛度隨法相載荷增大的速度不同;如圖5b所示,在分形維數大于1.4時,切向接觸剛度與法向載荷成線性關系,而當分形維數小于1.4之后,切向接觸剛度隨載荷增大的速率逐漸放緩(圖5a),與2.3節中的結論一致。 2.5接觸形式對切向接觸剛度的影響 當其他參數固定的情況下,接觸形式分別為外接觸和內接觸時,切向接觸剛度隨法向載荷的變化情況如圖6所示。由圖6可見,同等載荷作用下,內接觸形式的切向接觸剛度要大于外接觸形式的切向接觸剛度。 圖6 接觸形式對切向接觸剛度的影響(μ=0.3,D=1.9,G*=10-9,φ=0.005,R1=100 mm,R2=60 mm) 2.6球面曲率半徑對切向接觸剛度的影響 圖7給出了外嚙合時球面曲率半徑改變對切向接觸剛度的影響情況。由圖7可見,當設定球面1的曲率半徑R1=100mm不變時,隨著球面2的曲率半徑R2的減小,切向接觸剛度變小。 圖7 曲率半徑對切向接觸剛度的影響(μ=0.3,D=1.9,G*=10-9,φ=0.005) 以型號為6006的深溝球軸承的外圈與滾球接觸為例。滾動球體直徑[12]為7.144mm,外圈球形滾道半徑[13]為3.7506mm,摩擦因數[14]為0.0015~0.0022,鋼球等級[12]為G16,對應表面粗糙度Ra=0.025mm,根據文獻[15]中實驗數據,其表面分形參數為D=1.9752,G=1.0992×10-8mm,軸承鋼GCr15材料特性[16]為E=219GPa,υ=0.3,硬度為HBW190,應力σ=1700MPa,軸承承受徑向載荷為5000~8000N。圖8所示為軸承摩擦因數變化對軸承切向接觸剛度的影響,可以看出,摩擦因素對軸承的切向接觸剛度有較大影響,即隨著摩擦因數的增大,相同法向載荷下的接觸剛度減小。 圖8 摩擦因數對6006軸承切向接觸剛度的影響 (1)通過引入考慮摩擦因素的彈塑性變形的臨界面積計算公式,以兩球面接觸為研究對象,并基于切向接觸剛度的基本理論,建立了考慮摩擦因素時球面切向接觸剛度計算的分形模型,并對模型進行了仿真和分析。 (2)球面切向接觸剛度與法向載荷成正比關系。 (3)摩擦因數與球面切向接觸剛度的關系,受到分形維數的變化而呈現出不同的規律。當摩擦因數較小時,摩擦因數的變化對切向接觸剛度的影響較小,而當摩擦因數超過0.3后,切向接觸剛度對摩擦因數的變化敏感度提高。分形維數小于1.5時,切向接觸剛度隨摩擦因數的增大而減小;在分形維數大于1.5后,切向接觸剛度在摩擦因數取一較小定值時出現最大值。即分形維數較大,接觸面光滑,切向接觸剛度主要受摩擦因數影響;分形維數較小,表面較粗糙,切向接觸剛度主要受表面形貌影響。 (4)對分形維數1.1~1.9范圍內切向接觸剛度與法向載荷的關系進行了分析,分形維數小于1.5時,相同載荷情況下,切向接觸剛度隨著分形維數的增大而增大,而在分形維數大于1.5之后,分形維數與切向接觸剛度的關系成反比,即存在一個使接觸剛度達到最大值的分形維數。且在分形維數大于1.4時,切向接觸剛度與法相載荷成線性關系,而當分形維數小于1.4之后,切向接觸剛度隨載荷增大的速率逐漸放緩。在分形維數為1.5左右時,切向接觸剛度受法向載荷的影響敏感度增加,即相同法向載荷變化范圍,將引起切向接觸剛度的較大變化。 (5)材料特性參數決定于較軟材料的屈服強度,較軟材料的屈服強度增大,接觸表面能夠承受的切向力增大,因此,切向接觸剛度隨著材料的特性參數的增大而增大。 (6)粗糙度幅值增大將使切向接觸剛度減小;此外,由于粗糙度幅值與分形維數共同決定接觸表面的微觀形貌,因此,在不同分形維數下,粗糙度幅值對切向接觸剛度影響規律也不同。在分形維數大于1.4時,粗糙度幅值變化對切向接觸剛度影響明顯。 (7)球面內接觸比外接觸時的切向剛度大;隨著球體曲率在半徑的變大,切向剛度增大。 [1]張學良, 溫淑花. 基于接觸分形理論的結合面切向接觸剛度分形模型[J]. 農業機械學報, 2002, 33(3): 91-93. Zhang Xueliang, Wen Shuhua. A Fractal Model of Tangential Contact Stiffness of Joint Surfaces Based on the Contact Fractal Theory[J]. Transactions of the Chinese Society for Agricultural Machinery,2002, 33(3): 91-93. [2]田紅亮, 趙春華, 方子帆, 等. 基于各向異性分形理論的結合面切向剛度改進模型[J]. 農業機械學報, 2013, 44(3): 257-266. Tian Hongliang, Zhao Chunhua, Fang Zifan, et al. Improved Model of Tangential Contact Siffness for Joint Interface Using Anisotropic Fractal Theory[J]. Transactions of the Chinese Society of Agricultural Machinery, 2013, 44(3): 257-266. [3]田紅亮, 陳從平, 方子帆, 等. 應用改進分形幾何理論的結合部切向剛度模型[J]. 西安交通大學學報, 2014, 48(7): 46-52. Tian Hongliang, Chen Congping, Fang Zifan, et al. Tangential Stiffness Model for Joint Interface Adopting the Revised Fractal Geometric Theory[J].Journal of Xi’an Jiaotong University, 2014,48 (7): 46-52. [4]李小彭, 鞠行, 趙光輝, 等. 考慮摩擦因素的結合面切向接觸剛度分形預估模型及其仿真分析[J]. 摩擦學學報, 2013, 33(5): 463-468. Li Xiaopeng, Ju Xing,Zhao Guanghui, et al. Fractal Prediction Model of Tangential Contact Stiffness of Joint Surface Considering Friction Factors and Its Simulation Analysis[J]. Tribology, 2013, 33(5): 463-468. [5]趙韓, 陳奇, 黃康. 兩圓柱體結合面的法向接觸剛度分形模型研究[J]. 機械工程學報, 2011, 47(7): 53-58. Zhao Han, Chen Qi, Huang Kang. Fractal Model of Normal Contact Stiffness between Two Cylinders’ Joint Interfaces[J]. Journal of Mechanical Engineering, 2011, 47(7): 53-58. [6]陳奇, 趙韓, 黃康. 齒輪結合面切向接觸剛度分形計算模型研究[J]. 農業機械學報, 2011, 42(2): 203-206. Chen Qi, Zhao Han, Huang Kang. Fractal Model of Tangential Contact Stiffness between Gears’s Joint Surfaces[J]. Transactions of the Chinese Society of Agricultural Machinery, 2011, 42(2): 203-206. [7]Chen Q, Huang K, Zhao H, et al. Simulation and Analysis of the Model of Calculating Contact Tangential Stiffness between Cylinders’ Joint Interfaces by MATLAB[J]. Applied Mechanics and Materials, 2012, 190: 177-181. [8]Shi J, Cao X, Zhu H. Tangential Contact Stiffness of Rough Cylindrical Faying Surfaces Based on the Fractal Theory[J]. Journal of Tribology, 2014, 136(4): 041401. [9]Majumdar A, Bhushan B. Fractal Model of Elastic-plastic Contact between Rough Surfaces[J]. Journal of Tribology, 1991, 113(1): 1-11. [10]葛世榮, 朱華. 摩擦學的分形[M]. 北京: 機械工業出版社, 2005. [11]陳奇. 基于分形理論的汽車變速箱齒輪接觸強度研究[D]. 合肥: 合肥工業大學, 2010. [12]GB/T308-2002滾動軸承-鋼球[S].北京:中國標準出版社,2002. [13]郭明月. 深溝球軸承結構參數對振動規律影響的仿真與試驗研究[D].杭州: 中國計量學院,2014. [14]成大先.機械設計手冊(第五版)[M].北京:化學工業出版社,2010. [15]王薇. 分形理論在表面粗糙度非接觸測量中的應用[D].長春: 吉林大學,2006. [16]GB/T 18254-2002 高碳鉻軸承鋼[S].北京:中國標準出版社,2002. (編輯蘇衛國) Research on Fractal Model of TCS between Spherical Surfaces Considering Friction Factors Liu PengChen QiFan HaoHuang Shouwu Hefei University of Technology,Hefei,230009 In order to precisely calculate TCS between spherical surfaces, this paper presented the establishment of fractal model for TCS calculations between spheres considering friction factors. This model was obtained by introducing the equation of critical contact area of elasto-plastic deformation with friction and employing the basic theory of TCS, and based on the fractal contact model of two spherical surfaces. The numerical results show that: the TCS increases with normal loads; the relationship between TCS and friction coefficient is vary as the fractal dimension changes. It is efficient to improve the TCS by adding material propertied parameters and fractal roughness amplitude. The maximum value appears in TCS when the fractal dimension is 1.5 and the TCS increases significantly when the fractal dimension is about 1.5. Furthermore, TCS of inner contact is bigger than that of outer contact; TCS increases with curvature radius of cylinders. The theory herein helps to analyze the lubrication and dynamic characteristics between high-pair’s joint surfaces(like bearings) in the future. friction; spherical surface; tangential contact stiffness(TCS); fractal theory 2015-06-25 2015-09-25 國家自然科學基金資助項目(51305116) TH117.1 10.3969/j.issn.1004-132X.2016.20.014 劉鵬,男,1988年生。合肥工業大學機械工程學院博士研究生。研究方向新型傳動設計及接觸理論。陳奇,男,1979年生。合肥工業大學機械工程學院副教授。樊浩,男,1993年生。合肥工業大學機械工程學院碩士研究生。黃守武,男,1991年生。合肥工業大學機械工程學院碩士研究生。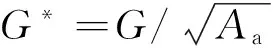
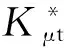
2 模型的仿真與分析
3 算例
4 結論

