駐波法測聲速時兩種數據處理方法的對比研究*

張松鋒　周小東

(周口師范學院機械與電氣工程學院　河南 周口　466001)

?

駐波法測聲速時兩種數據處理方法的對比研究*

張松鋒周小東

(周口師范學院機械與電氣工程學院河南 周口466001)

駐波法是常用的聲速測量方法.駐波法測聲速時常用逐差法進行數據處理，也有采用最小二乘法的，為了比較兩種方法的優劣，本文對駐波法測聲速分別采用逐差法和最小二乘法處理數據，并對測量結果的不確定度進行了分析.通過數據處理結果發現，逐差法和最小二乘法在駐波法測聲速的數據處理上是等效的，都能得到良好的效果.

聲速測量駐波法逐差法最小二乘法

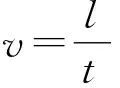
1　實驗原理[4～8]

如圖1所示，從發射換能器S1發出一定頻率的平面波，經過空氣傳播一段距離后到達接收換能器S2.如果兩個換能器的接收平面和發射平面平行，平面波到達接收面后會發生反射，如此循環往復，因此在示波器中看到的波形應該是入射波和反射波在兩個端面間來回反射并疊加而形成的波形，雖然疊加波并非理想駐波，但疊加波的相鄰波腹(或波節)之間的距離剛好等于半波長的整數倍，即疊加波形中相鄰極大值(或極小值)之間的距離為半個波長.可使用測試儀上的數顯尺測出n個半波長的長度l，從信號發生器上讀出發射聲波的頻率f，則聲速為

(1)

圖1　聲速測量裝置

空氣中的聲速與環境溫度和濕度有關，若只考慮溫度的影響，聲速的理論計算式為

(2)

其中t為環境溫度，采用攝氏溫標，T0=273.15 K，v0為0℃時的聲速，對于空氣介質v0=331.45 m/s.根據式(2)可計算出溫度為t時空氣中聲速的理論值.

2　數據原始記錄

采用駐波法測聲速時，要測的物理量有測試系統的最佳工作頻率和接收端波形出現極大值時數顯尺的讀數，分別如表1和表2所示.環境溫度t=13.2℃.

表1　測試系統的最佳工作頻率

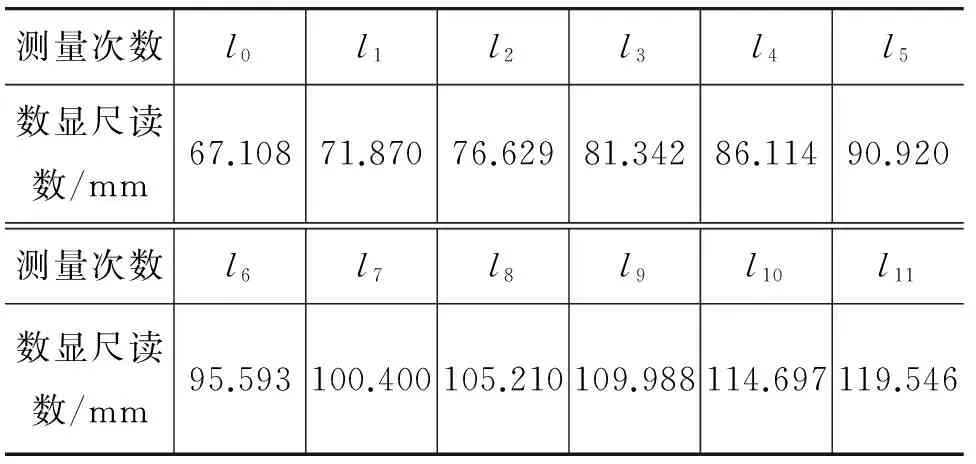
表2　波形出現極大值時數顯尺讀數

3　數據處理及分析[7,8]

3.1逐差法

按照逐差法處理實驗數據的原理，根據表2數據求解波長，如表3所示.

表3　λi值

代入數據得

v1=342.218 m/s

(1)A類不確定度分析

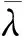
所以

(2)B類不確定度分析

儀器讀數分辨率引入的誤差按B類評定，數顯尺的最小分度為0.01 mm，估讀值為0.005 mm，即Δ=0.005 mm.

(3)合成不確定度分析

根據不確定度合成公式可得

3.1.2頻率f的不確定度分析

(1) A類不確定度分析

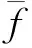
(2)B類不確定度分析

信號發生器中頻率的最小分度為0.001 kHz，所以Δ=0.000 5 kHz.

(3)合成不確定度分析

根據不確定度合成公式可得

3.1.3聲速v的不確定度分析

聲速v的不確定度傳遞公式為

所以聲速的不確定度為

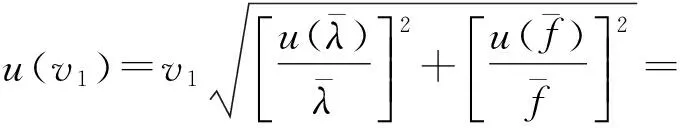
v1±u(v1)=(342.2±0.3) m/s

環境溫度為13.2℃時，聲速的理論值vs為339.364 m/s，所以測量值的相對誤差

3.2最小二乘法

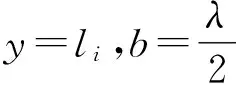
關聯系數

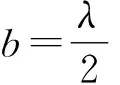
v2=λf=342.326 m/s

3.2.1波長不確定度分析

(1) A類不確定度分析

b的標準偏差為

所以

uA(λ)=Sb=0.001 4 mm

(2)B類不確定度分析

B類不確定度和采用逐差法時一樣，所以

uB(λ)=0.002 9 mm

(3)合成不確定度分析

3.2.2聲速的不確定度分析

0.1 m/s

測量結果為

v2±u(v2)=(342.3±0.1) m/s

所以測量值的相對誤差

4　結論

從逐差法和最小二乘法處理數據的結果來看，二者在處理駐波法測聲速實驗數據時都可以得到較好的結果，因為利用二者計算的結果和理論值的誤差都小于1%，在誤差允許的范圍內，并且二者的誤差相差不大，只有0.03%.所以利用逐差法和最小二乘法處理數據是等效的.

1吳定允，常加忠.大學物理實驗.鄭州：河南科學技術出版社，2014.138～141

2眭聿文.聲速測量實驗中聲波的研究.西華大學學報(自然科學版)，2011，30(1)：52～55

3王山林.關于聲速測量實驗的研究與設計.廊坊師范學院學報(自然科學版)，2012，12(1)：45～46

4潘健，姚淅偉.關于聲速測量實驗的討論.大學物理，2010，29(11)：55～58

5鄭慶華，童悅.聲速測量實驗的理論分析.宜春學院學報(自然科學版)，2006，28(4)：44～46

6張俊玲.駐波法測量聲速實驗的系統誤差分析.大學物理實驗，2012，25(5)：81～83

7劉石劬.聲速測量及不確定度分析.大學物理實驗，2013，26(4)：99～103

8黃賢群.基于最小二乘法的聲速測定實驗數據處理及分析.大學物理實驗，2012，25(2)：75～77

張松鋒(1981-)，男，碩士，講師，主要研究方向為基礎物理實驗的教學與研究.

2016-04-13)

*國家自然科學基金“金屬納米顆粒表面等離激元增強半導體發光機理研究”，項目編號：11405280；河南省教育廳科學技術研究重點項目“金屬納米顆粒局域表面等離激元增強半導體發光性能研究”，項目編號：14B140021