天體運動的幾種模型

李良偉

(江西省石城中學　江西 贛州　342700)

?

天體運動的幾種模型

李良偉

(江西省石城中學江西 贛州342700)

天體運動有4種模型，本文以2015年部分高考試題為例，總結出各種天體運動模型的運動和受力特點，以期舉一反三.

天體運動模型運動特點受力特點

天體運動是高考中必考的內容之一，一般以選擇題形式出現.天體運動形式多樣,公式變化繁雜,題目設計問法多樣,數據計算復雜，因而學生普遍感到學習困難.從物體受力與運動關系出發，緊扣萬有引力與向心力的關系，便可迅速找到解題方法.天體運動一般有以下幾種模型.

1　勻速圓周運動模型

1.1圍繞中心天體做勻速圓周運動

行星或衛星圍繞中心天體做勻速圓周運動時，其軌道平面一定過中心天體中心，萬有引力等于向心力(F引=man)，此時重力與萬有引力相等(mg′=F引)，也就有mg′=man.

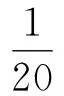
A．1∶10 B．1 C．5D．10

解析：由題意知，“51 peg b”繞其中心恒星做勻速圓周運動，有

化簡得

可得恒星質量與太陽質量之比約為1，所以B正確.

1.2雙星模型

在遠離其他天體的空間中，兩顆離得較近的天體圍繞它們連線上某點做勻速圓周運動時，兩顆星體的角速度一定相等，萬有引力等于向心力(F引=man).特別注意兩天體之間的距離等于兩天體做勻速圓周運動的軌道半徑之和.

瓷器的裝飾紋飾有兩大類：一類繼承陶器裝飾傳統，以圖案飾之；一類則是創新，彩繪中國畫。無論是繼承，還是創新，以表達人類的思想情感為主旨的理念沒變。

【例2】神奇的黑洞是近代引力理論所預言的一種特殊天體，探尋黑洞的方案之一是觀測雙星系統的運動規律.天文學家觀測河外星系大麥哲倫云時，發現了LMCX-3雙星系統，它由可見星A和不可見的暗星B構成.兩星視為質點，不考慮其他天體的影響，A，B圍繞兩者連線上的O點做勻速圓周運動，它們之間的距離保持不變，如圖1所示.引力常量為G，由觀測能夠得到可見星A的速率v和運行周期T.恒星演化到末期，如果其質量大于太陽質量ms的2倍，它將有可能成為黑洞.若可見星A的速率v=2.7×105m/s，運行周期T=4.7π×104s，質量m1=6ms，試通過估算來判斷暗星B有可能是黑洞嗎？(G=6.67×10-11N·m2/kg2，ms=2.0×1030kg)

圖1

解析：由題意知，A，B兩星構成“雙星”模型，設A，B的圓軌道半徑和質量分別為r1，r2和m1，m2，A，B兩星間距為r=r1+r2，對可見星A有

又因為

m1ω2r1=m2ω2r2

得

r1∶r2=m2∶m1

以上關系式可得

設m2=nms，(n>0)，將其和m1=6ms及相關數據代入上式，得

(1)

(2)

由式(2)可知，若使式(1)成立，則n必須大于2，即暗星B的質量m2必須大于2ms，由此得出結論：暗星B有可能是黑洞．

1.3三星模型

在遠離其他天體的空間存在3顆星體，它們以受到的萬有引力的合力為向心力做勻速圓周運動，三星的角速度也一定相等.

【例3】(2015年高考安徽卷第24題)由3顆星體構成的系統，忽略其他星體對它們的作用，存在著一種運動形式:3顆星體在相互之間的萬有引力作用下，分別位于等邊三角形的3個頂點上，繞某一共同的圓心O在三角形所在的平面內做相同角速度的圓周運動(圖2所示為A，B，C三顆星體質量不相同時的一般情況).若A星體質量為2m，B和C兩星體的質量均為m，三角形邊長為a.求：

(1)A星體所受合力大小FA；

(2)B星體所受合力大小FB；

(3)C星體的軌道半徑RC；

(4)三星體做圓周運動的周期T.

圖2

解析：(1)由萬有引力定律，A星體所受B，C星體引力大小為

方向如圖3，則合力大小為

圖3

(2)同上，B星體所受A,C星體引力大小分別為

方向如圖3，則合力大小為

可得

(3)通過分析可知，圓心O在中垂線AD的中點

(4)三星體運動周期相同，對C星體由

可得

1.4地面模型

如圖4所示，放在地面的物體A隨著地球一起做勻速圓周運動，軌道平面為某一緯度平面，萬有引力沿軌道平面指向地軸的分力等于向心力Fn，另一分力則為重力mg.由于地球的自轉速度較小，向心力大約只有萬有引力的0.34%，故可認為mg=F.在其他星球表面情況類似.

圖4

【例4】(2015年高考新課標Ⅰ卷第21題)我國發射的“嫦娥三號”登月探測器靠近月球后，先在月球表面附近的近似圓軌道上繞月運行；然后經過一系列過程，在離月面4 m高處做一次懸停(可認為是相對于月球靜止)；最后關閉發動機，探測器自由下落，已知探測器的質量約為1.3×103kg，地球質量約為月球質量的81倍，地球半徑約為月球半徑的3.7倍，地球表面的重力加速度約為9.8 m/s2,則此探測器

A. 著落前的瞬間，速度大小約為8.9 m/s

B. 懸停時受到的反沖作用力約為2×103N

C. 從離開近月圓軌道這段時間內，機械能守恒

D. 在近月圓軌道上運行的線速度小于人造衛星在近地圓軌道上運行的線速度

解析:在中心天體表面上萬有引力提供重力

則可得月球表面的重力加速度

根據平衡條件，探測器懸停時受到的反作用力F=G探=m探g月≈ 2×103N，選項B正確；探測器自由下落，由v2=2g月h,得出著落前瞬間的速度v≈3.6 m/s ,選項A錯誤；從離開近月圓軌道，關閉發動機后，僅在月球引力作用下機械能守恒，而離開近月軌道后還有制動懸停，發動機做了功，機械能不守恒，故選項C錯誤；在近月圓軌道萬有引力提供向心力

解得運行的線速度

小于近地衛星線速度，選項D正確.

2　橢圓軌道模型

行星或衛星圍繞中心天體運動的軌道是橢圓時，萬有引力不等于向心力，在近地點，萬有引力小于向心力，做離心運動；在遠地點，萬有引力大于向心力，做向心運動.

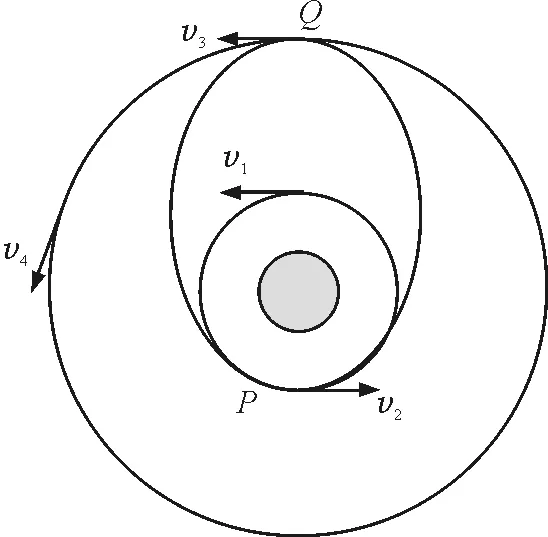
圖5

【例5】如圖5所示，發射同步衛星的一般程序是：先讓衛星進入一個近地的圓軌道，然后在P點變軌，進入橢圓形轉移軌道(該橢圓軌道的近地點為近地圓軌道上的P，遠地點為同步圓軌道上的Q)，到達遠地點Q時再次變軌，進入同步軌道．設衛星在近地圓軌道上運行的速率為v1，在橢圓形轉移軌道的近地點P的速率為v2，沿轉移軌道剛到達遠地點Q

2016-04-11)