電場強度在帶電表面突變問題的深入探討

劉 倩　翟曉霞　艾麗娜

(石家莊理工職業學院　河北 石家莊　050200)

?

電場強度在帶電表面突變問題的深入探討

劉 倩翟曉霞艾麗娜

(石家莊理工職業學院河北 石家莊050200)

討論了應用高斯定理求解帶電球面和帶電球體電場強度分布的問題，并對其結果關于電場強度在球面上突變的問題進行了分析討論，利用“面模型”解釋了產生突變的原因.

高斯定理電場強度突變面模型

1　引言

高斯定理是靜電場中的普遍規律，在靜電場場強計算中有著重要的應用.在真空中高斯定理的表達式[1]為

它表明電場中通過任一閉合曲面的電通量等于該曲面內所有電荷量的代數和除以ε0，與閉合曲面外的電荷無關.對于電荷分布均勻并且對稱的帶電體，可以應用高斯定理求出帶電體電場強度的分布[2].本文利用高斯定理求出了帶電球面和帶電球體周圍的電場強度分布，并通過對場強分布的分析發現帶電球面內外的場強存在突變，在文中利用“面模型”解釋了電場強度在帶電面上的突變問題.最后總結了將帶電面看做“面模型”的條件.

2　高斯定理求解均勻帶電球面和帶電球體的電場強度分布

【例1】電荷q均勻分布于半徑為R的球面上，求球內外的靜電場強分布.

從電荷分布的球對稱性出發，不難證明球形高斯面S上各點場強大小相等，方向沿徑向[3]，那么如圖1，S面的E通量

球形高斯面內的電荷為q，由高斯定理

可以得到

方向沿徑向.

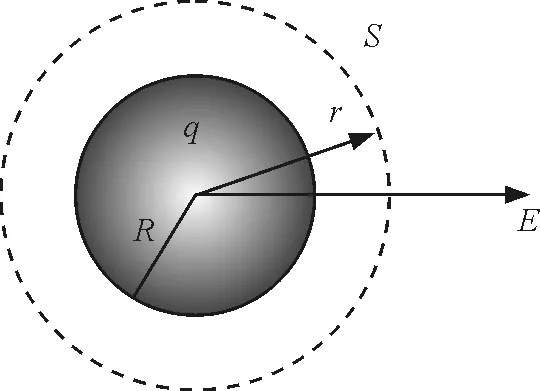
圖1　用高斯定理求均勻帶電球面的場強

對于球面內的電場，在球面內做一個球形高斯面，由于高斯面內的電荷為零[4]，故

En4πr2=0

因而E=0.

由以上結果可以畫出場強大小E隨r變化的函數曲線如圖2所示.

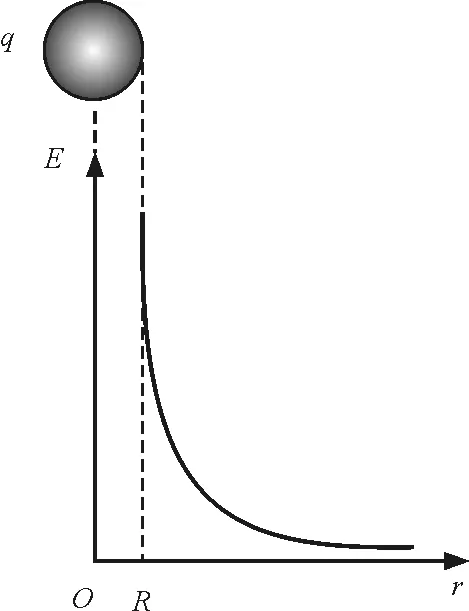
圖2　均勻帶電球面的場強分布曲線

【例2】電荷q均勻分布于半徑為R的球體上，求球體內外的場強分布.

仿照例1的情況，根據對稱性可以運用高斯定理求出球外場強仍為

球內場強為

球內外場強大小隨r的變化曲線如3所示.

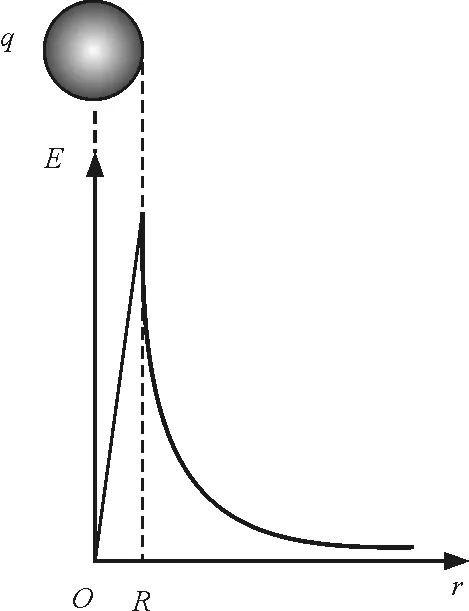
圖3　均勻帶電球體的場強分布曲線

由以上兩例可知，應用高斯定理可以很方便地求解出具有對稱性的帶電體周圍的電場強度分布.由圖3可看出均勻帶電球體的場強在球內、球外以及球面都是連續的矢量場，但是圖2卻表明均勻帶電球面的場強在面上有突變.

3　對帶電球面場強突變問題的分析討論

上述兩例表明，與帶電球體不同，帶電球面的場強在面上有突變.這種突變是場強在帶電面上采用面模型的結果，面模型即帶電薄層的簡化，場強從薄層的一壁到另一壁是連續變化的，只是由于簡化成面模型(薄層厚度為零)才出現突變[3].現以均勻帶電的同心球層為例來說明突變的問題.

如圖4所示，球層的內外壁把空間分為3個區：rR2為C區，由高斯定理不難求出A，B，C3區的場強EA,EB,EC為

EA=0

其中ρ及q分別為球層的電荷體密度和電荷量.由三區場強的結果畫出的E-r曲線如圖4所示，從圖中可以明顯看到是一條連續的曲線，在任何半徑r處都無突變，球層內外壁(r=R1及r=R2)處場強的差值為

圖4　均勻帶電球層的場強(厚度較大)

在用高斯定理求解帶電球面的場強分布時采用的是帶電面模型，帶電面模型是把帶電薄層的電荷集中于一個幾何面上得到的，現在保持球層總的電荷量不變，令R1趨近于R2，由上面ΔE的表達式可知，ΔE的值并不改變，如圖5所示.

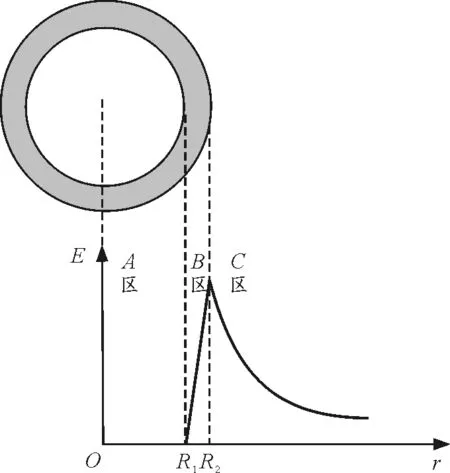
圖5　均勻帶電球層的場強(厚度較小)

在極限情況下有

即球層薄至成一個幾何面時(電荷不變)，內外壁的場強差值仍為一有限值，如圖6所示，分居球面兩側的兩個極近點的場強有一個有限差值，也就意味著場強在帶電球面上發生突變.

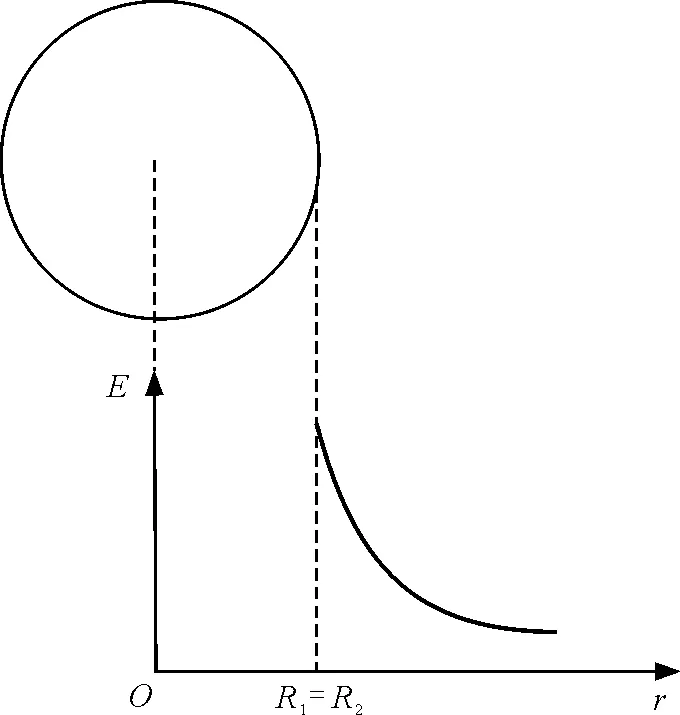
圖6　均勻帶電球層的場強(厚度為零，即帶電球面)

由以上分析可知，帶電球面上場強存在突變是由于將帶電面的厚度簡化為零得到的結果.然而面模型是有條件的，條件是場點與薄層的距離遠大于層的厚度，若討論面上的一點場強就不能采用面模型，因為涉及這個點的帶電層已經不能看成幾何面了.

4　結論

在物理學的研究中經常會找到一些物理模型來簡化研究過程，在教學中也可以讓學生更加清晰地理解物理過程.采用簡化模型是有條件的，本文中采用的是面模型，條件是場點與薄層的距離遠大于層的厚度.但是如果不關心帶電層內及其附近的場強是否表達得很準確，那么可以對整個空間采用面模型，于是就出現本文中討論的電場在面上的突變問題.

1趙凱華,等. 電磁學(上冊). 北京：高等教育出版社, 1998.52～54

2衛麗娜. “電場高斯定理”的教學設計. 物理通報,2015(8):22

3梁燦彬, 秦光戎. 電磁學. 北京：高等教育出版社, 2004.22～23

劉倩(1985-)，女，碩士，講師,主要從事基礎物理教學以及多鐵性納米材料的研究.

2016-03-27)