爆炸條件下結構超壓-沖量曲線簡化計算研究

陳俊杰， 高康華, 孫　敖

(1.解放軍理工大學 爆炸沖擊防災減災國家重點實驗室，南京　210007; 2.總參工程兵科研三所，洛陽　471023)

爆炸條件下結構超壓-沖量曲線簡化計算研究

陳俊杰1， 高康華1, 孫敖2

(1.解放軍理工大學 爆炸沖擊防災減災國家重點實驗室，南京210007; 2.總參工程兵科研三所，洛陽471023)

超壓-沖量(P-I)曲線可用于快速評估爆炸荷載作用下建筑結構的毀傷效應。基于單自由度等效體系運動方程和結構變形的理想彈塑性模型，在傳統能量法基礎上考慮阻尼影響，運用圖像法計算阻尼耗能，得到了P-I曲線沖量區和準靜態區的漸進線方程，在此基礎上通過大量計算，得到了P-I曲線動態區的擬合公式。提出的簡化計算公式與運用Newmark β法計算結構響應得到的P-I曲線相比較為一致，驗證了所提方法的合理性。通過算例表明，隨著延性比的增大，P-I圖的沖量漸近線和準靜態漸近線的值逐漸變小；隨著阻尼比的增大，P-I圖的沖量漸近線和準靜態漸近線的值逐漸變大，且阻尼比對沖量漸近線影響明顯。

超壓-沖量(P-I)曲線;單自由度等效體系；理想彈塑性模型；阻尼；損傷評估

當前恐怖爆炸襲擊和偶然性爆炸事故的不斷發生，對人民生命和財產造成了極大的威脅。研究爆炸荷載對結構的破壞效應，對結構的抗爆設計和毀傷評估具有極其重要的意義。超壓-沖量(P-I)曲線，又稱等毀傷曲線，是通過結構動力響應計算確定給定破壞條件下一系列的超壓和沖量，以此兩個參數為坐標繪制P-I曲線圖，描述最大響應值和動力系統特征參數的關系，可用于快速評估特定爆炸荷載作用下建筑結構的響應和毀傷效應[1-4]。針對P-I曲線的建立，許多學者展開了研究：Baker等[2]通過能量法得到彈性、剛塑性模型的P-I曲線的沖量區和準靜態區圖形，并提出了動態區的公式。Oswald等[3]通過類似方法，得到了理想彈塑性模型的P-I曲線的沖量區和準靜態區圖形，并提出了相應的動態區公式。Krauthammer等[4-5]通過求解封閉方程，直接求得彈性體系的等效P-I曲線方程。Li等[6-7]通過無量綱分析的方法，得到了彈性和彈塑性體系下歸一化的P-I曲線，消除了荷載形狀對P-I圖的影響。Fallah等[8]在此基礎上研究了彈塑性硬化和彈塑性軟化模型的P-I曲線，Ma等[9]提出了一種同時考慮彎曲破壞和剪切破壞的P-I曲線確定方法，汪維等[10]提出了基于SDOF體系基礎上鋼筋混凝土構件考慮彎曲和剪切失效模式建立P-I曲線的方法，并給出相應的經驗公式。隨著計算機的發展，許多國內外學者通過LS-DYNA、ABAQUS等有限元程序分析了鋼筋混凝土構件的P-I曲線。李忠獻等[11]給出了混凝土板的P-I曲線，Huang等[12]給出了混凝土梁、柱的P-I曲線，師燕超等[13]給出了混凝土柱的P-I曲線，Wu[14]考慮了泡沫鋁加強的混凝土構件的P-I曲線，Mutalib等[15]給出了FRP加強的混凝土柱的P-I曲線。Huang等[16]給出考慮多種失效模式的混凝土構件的P-I曲線。總的看來，P-I曲線主要基于結構動力響應分析得到，運用有限元等數值方法獲取完整的P-I曲線需進行大量計算[4]。將結構視為單自由度等效體系(SDOF)，運用能量法獲取P-I曲線時可使計算量大大減少，是當前計算P-I曲線時快速有效的方法，但目前多數基于SDOF假設計算P-I曲線的研究中均未考慮阻尼的影響。

本文在傳統能量法的基礎上進一步考慮阻尼耗能，基于SDOF無量綱動力方程和結構變形的理想彈塑性模型，運用Newmark-β數值計算方法進行了大量計算，提出了快速計算P-I曲線的簡化方法，為建筑結構、構件的抗爆設計和快速損傷評估提供理論參考和技術支持。

1　基本理論

1.1單自由度等效模型

單自由度等效模型是將實際構件簡化為單自由度等效體系，運動方程可按下式表示：

(1)

圖1　簡化的爆炸荷載的壓力時程曲線Fig.1 Load time history curve of simplified explosive load

圖2　理想彈塑性模型的抗力函數Fig.2 Resistant function of elastic perfectly-plastic model

為方便計算分析，選取一組無量綱參數，如式(2a)～(2g)：

(2a)

(2b)

(2c)

(2d)

(2e)

(2f)

(2g)

將式(2a)～(2g)代 入式(1)，可得

(3)

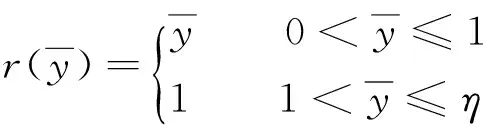
(4a)

對于圖1所示三種荷載形式有

(4b)

其中當為矩形荷載時，λ=0,γ=0；當為三角形荷載時，λ=1,γ=0；當為指數形荷載時，λ=1,γ=2.8。

(5a)

(5b)

將初始條件式(5a)，式(5b)代入方程式(3)，由于0≤ξ<1，可以解得

(6)

將式(6)對τ求導，得

(7)

(8)

因此當τ=τe時的速度為

(9)

(10a)

(10b)

將初始條件式(10a)，式(10b)代入方程式(3)，可以解得

① 當ξ=0時

(11)

式(11)對τ求導，得

(12)

② 當ξ>0時

(13)

式(13)對τ求導，得

(14)

隨τ的變化

隨τ的變化圖3　無量綱的位移時程和速度時程曲線Fig.3 The dimensionless time history curves of dimensionless displacement and dimensionless speed

1.2P-I圖的特點及能量法

P-I曲線通常基于SDOF方法，假設構件為彎曲破壞形式，根據結構中點的最大撓度和確定的破壞等級，確定一系列對應的超壓和沖量。通常引入以下無量綱形式的壓力和沖量

(15a)

(15b)

若定義無量綱沖量i為

(16)

將式(2a)，式(2e)，式(2f)代入式(16)，則有

(17)

將式(17)代入式(15a)，式(15b)，得

(18a)

(18b)

因此為了求解一定荷載形式下，特定延性比ηc和阻尼比ξ的P-I曲線，只需保持其他條件不變，通過改變荷載條件p和τd組合后求解方程式(3)，使得

(19)

圖4為無量綱P-I曲線的示意圖，P-I曲線將圖分為兩個區域，曲線左下方區域(圖中區域Ⅰ)，即曲線與坐標軸之間的區域，表示未到達破壞等級；曲線右上方區域即圖中區域Ⅱ，表示超過破壞等級。P-I曲線從上到下分別為沖量區，動態區和準靜態區，在沖量區和準靜態區的漸近線分別有垂直和水平的漸近線。

圖4　結構構件典型P-I曲線示意Fig.4 Typical P-I curve of a structural member

能量法通過能量守恒原理可快速確定P-I曲線的準靜態漸近線和沖量漸近線。在準靜態區，荷載持續的時間很長，結構達到最大位移前荷載衰減較小，該階段外力做功可近似與體系應變能相等。外力可能的最大功為：

W.E=Fmym

(20)

應變能為抗力位移曲線所圍面積

(21)

假設準靜態區內外力做功全部轉化為應變能

W.E=S.E

(22)

將式(20)～(22)聯立，得到P-I曲線的準靜態漸近線。

而在沖量區內，荷載持續時間很短，荷載結束后體系位移很小，因此可近似認為在此階段內，動能全部轉化為應變能。零時刻體系無應變能，輸入的動能為

(23)

零時刻的動能最終轉化為應變能

K.E=S.E

(24)

將式(21)，式(23)，式(24)聯立，得到P-I曲線的沖量漸近線。

對于理想彈塑性模型應變能可寫為

(25)

將式(25)代入式(20)～(24)中，可得到不考慮阻尼情況下理想彈塑性模型P-I曲線準靜態漸近線和沖量漸近線的值。

2　P-I曲線的計算方法

對鋼筋混凝土結構，爆炸荷載作用下結構最大位移通常出現在第一個振動周期內，此時阻尼對響應的影響較小，為此傳統能量法計算P-I曲線漸近線時通常不計阻尼影響。但實際上系統阻尼是存在的，本文考慮阻尼對結構振動的影響，在傳統能量法基礎上引入阻尼耗能，確定考慮阻尼時P-I曲線的漸近線的方程。

由于P-I曲線反映的是結構的最大位移，所以此時阻尼耗能D.E可以表示為

(26)

將式(2b)，式(2c)代入式(26)得到

(27)

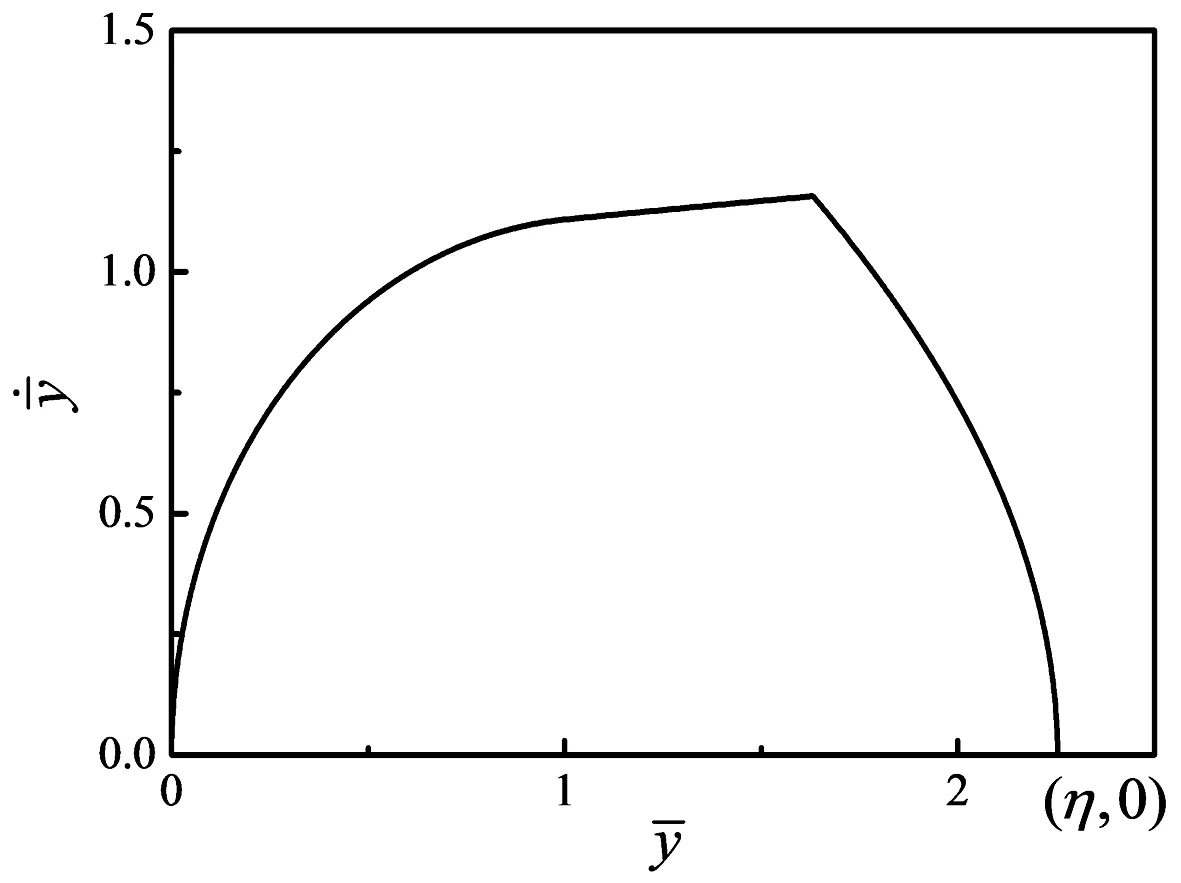
圖5　無量綱速度位移曲線Fig.5 Dimensionless velocity displacement curve

若令

(28)

則有

(29)

(a) 不同區域的影響(b) 準靜態區不同點的影響(c) 沖量區不同點的影響

(d) 阻尼比的影響(e) 荷載形狀的影響圖6 無量綱速度位移曲線的影響因素Fig.6Theinfluencefactorsofdimensionlessvelocitydisplacementcurve

表1　阻尼比對S的影響

表2　荷載形狀對S的影響

由性質(3),(4)可知，阻尼比和荷載形狀對S值很小。

2.1準靜態區漸近線方程的求解

圖7　準靜態區的無量綱速度位移曲線隨延性比的變化Fig.7 Dimensionless velocity displacement curve of quasi-static region changing with the ductility ratio

由圖7可知，每種情況的圖像大致可以為一段1/4圓和一個段不規則曲線，但對不同的η，該圖像的形狀有一定的差別。計算η=1,1.5,2,3,4,5時對應的S值，見表3。

表3　延性比準靜態區的S值的影響

觀察表3可知，S值大致為η的一次函數。以η為自變量，對S值進行擬合。

圖8　準靜態區S值與延性比的關系Fig.8 The relationship between quasi-static region S value and the ductility ratio

圖8為計算點與擬合公式的對比，可見擬合效果較好，因此準靜態區S值可以下式計算

S=0.677 2η-0.267 6

(30)

將求得的S值代入式(29)求得阻尼耗能。假設該階段外力功全部轉化為應變能和阻尼耗能

W.E=S.E+D.E

(31)

將式(20)，式(25)代入，得到準靜態區的漸近線方程

(32)

其中S按式(30)計算。

2.2沖量漸近線的求解

圖9　準靜態區的無量綱速度位移曲線隨延性比的變化Fig.9 Dimensionless velocity displacement curve of impulse region changing with the ductility ratio

延性比11.52345S0.7761.5912.5504.7927.45210.465

觀察表4可知，S值大致為η的指數型函數。以η為自變量，對S值進行擬合。

圖10　沖量區S值與延性比的關系Fig.10 The relationship between impulse region S value and the ductility ratio

圖10為計算點和擬合數據的對比，可以看出公式擬合效果較好，因此沖量區區S值可以下式計算

S=0.864 5η1.551

(33)

將式(33)代入式(29)，可以得到動態區的阻尼耗能D.E。

假設系統零時刻的動能全部被應變能和阻尼耗能吸收，則

K.E=S.E+D.E

(34)

將式(23)，式(25)代入，得到沖量區的漸近線方程為

(35)

其中S按式(33)計算。

對于式(32)，式(35)，令ξ=0可以得到無阻尼理想彈塑性體系的準靜態漸近線和沖量漸近線的方程，與文獻[8]結果一致。

2.3動態區擬合公式

能量法僅能確定準靜態區和沖量區的漸近線方程，而動態區P-I曲線一般呈雙曲線形式，文獻[3][4]給出了等效P-I曲線動態區的公式：

(36)

圖11　無阻尼時的擬合曲線與計算值對比Fig.11 Fitting curve compared with calculated value under undamped condition

而當在P-I曲線中加入阻尼的影響時，擬合曲線時不但要考慮阻尼對漸近線值的影響，也要考慮阻尼對曲線形狀的影響，而改變式(36)中的參數無法改變曲線的形狀。對無阻尼的理想彈塑性體系，式(36)的C，D為常數，因此不妨假設考慮阻尼的動態區公式具有如下的形式：

(37)

式(37)中A，B分別表示準靜態漸近線和沖量漸近線的值，用式(32)(34)計算出，C為荷載形狀影響的常數，n為受ξ和η影響的參數。對矩形荷載的取C=0.015 5。

這樣，式(37)中只有一個n為未知量。通過式(19)給出的方法，可以計算出P-I上的點。以η=1,2,3，ξ=0,0.05,0.1的9種情況為參照，將其P-I曲線的點計算出來，再用式(37)對每個P-I曲線進行擬合。表5為擬合的計算過程和結果，其中每一組的平方差均大于0.98。以ξ和η為變量，對n進行擬合。可以得到的n擬合公式為

n=1.061+0.091 55η+0.052 97ξ+

0.051 92ξη+0.008 2ξ2

(38)

其中擬合的R2=0.957。

表5　擬合計算結果

這樣得到了矩形荷載作用下，考慮延性比和阻尼比理想彈塑性體系的動態區擬合公式。按照同樣方法，可以求出三角形荷載和指數形荷載作用下的參數n，建立相應的P-I曲線動態區擬合公式。

3　算例分析

3.1算法對比

文獻[4-5]驗證了使用數值方法計算P-I曲線時有較好的精度，同時文獻[4]也指明了使用數值方法計算P-I曲線需要較大的計算量和較高的精度。在動力分析中，鋼筋混凝土結構的延性比一般不超過5，阻尼比也一般介于5%～10%之間。通過算例，取常見的兩種工況，將本文方法與文獻[4-5]提出的數值方法計算出的P-I曲線進行對比。

圖12　數值方法和擬合公式結果對比Fig.12 The results of numerical method and the fitting formula

從圖12可以看出，兩種方法總體上吻合程度較好。從表6可以看出，在沖量區和準靜態區，擬合公式相對偏差小于2%，在動態區誤差也在5.51%內，總體偏差在10%內，體現了公式較好的適用性。使用數值方法建立P-I曲線需要大量的計算，本文方法在保證精度地同時可以大大減小計算量，更加快速的建立P-I曲線。

3.2參數影響分析

為了分析參數的影響，以式(32)、(35)、(37)、(38)為基礎，對矩形荷載作用下的不同延性比和阻尼比的理想彈塑性體系，建立并分析其P-I曲線，研究延性比和阻尼比對P-I曲線的影響。

3.2.1延性比

保持阻尼比不變，研究延性比對P-I曲線的影響。圖13為ξ=0，η=1,2,3,4時將所得的P-I曲線。可以看出，隨著延性比的增大，P-I圖的沖量漸近線和準靜態漸近線的值變小。對于彈性極限位移一定的構件，延性比越大構件越不易被破壞。

圖13　延性比對P-I曲線的影響Fig.13 Influence of ductility ratio on P-I curves

計算方法第一組A點B點C點第二組D點E點F點數值方法1.02030.61240.42860.73910.82360.4286擬合公式1.01910.61060.43540.75270.86900.4354相對偏差/%-0.12-0.291.591.855.511.59

3.2.2阻尼比

圖14　阻尼比對P-I曲線的影響Fig.14 Influence of damping ratio on P-I curves

4　結　論

(1) 在能量法基礎上，加入阻尼耗能的影響，運用無量綱的運動分析，求解了考慮阻尼情況下理想彈塑性模型的P-I曲線漸近線方程，并給出了P-I曲線的動態區擬合公式。以數值方法為參考，對擬合公式進行了驗證，結果表明了擬合公式與數值方法較好的一致性，可以運用擬合公式快速建立P-I曲線。

(2) 隨著延性比的增大，P-I圖的沖量漸近線和準靜態漸近線逐漸變小。提高構件的延性比，可以提高構件的抗爆性能。

(3) 隨著阻尼比的增大，P-I圖的沖量漸近線和準靜態漸近線逐漸變大。阻尼比對沖量漸近線影響明顯，說明提高構件阻尼比，可以提高構件的抗爆性能。

[1] Wesevich J W, Oswald C J. Empirical based concrete masonry pressure-impulse diagrams for varying degrees of damage [C]//American Society of Civil Engineers, 2005, 2083-2094.

[2] Baker W E, Cox P A,Westine P S, et al. Explosion Hazards and Evaluation [M]. Amsterdam, New York: Elsevier Scientific Pub. Co., 1983.

[3] Oswald C J, Skerhut D. FACEDAP User’s Manual [M]. Omaha: Southwest Research Institute and U.S. Army Corps of Engineers, 1993.

[4] Krauthammer T. Modern protective structures [M]. Boca Raton, London, New York:CRC Press, 2008.

[5] Krauthammer T, Astarlioglu S, Blasko J, et al. Pressure-impulse diagrams for the behavior assessment of structural components[J]. International Journal of Impact Engineering, 2008, 35(8): 771-783.

[6] Li Q M, Meng H． Pulse loading shape effects on pressure-impulse diagram of an elastic-plastic, single-degree-of-freedom structural model [J]. International Journal of Mechanical Sciences, 2002, 44(9): 85-98.

[7] Li Q M,Meng H. Pressure-impulse diagram for blast loads based on dimensional analysis and single-degree-of-freedom model [J]. Journal of Engineering Mechanics (ASCE), 2002, 128(1): 87-92.

[8] Soleiman F A, Louca L A. Pressure-impulse diagrams for elastic plastic hardening and softening single-degree-of-freedom models subjected to blast loading [J]. International Journal of Impact Engineering, 2007, 34(4): 823-842.

[9] Ma G W, Shi H J, Shu D W. P-I diagram method for combined failure modes of rigid-plastic beams [J]. International Journal of Impact Engineering, 2007, 34(6): 1081-1094.

[10] Wang W, Zhang D, Lu F Y, et al. Pressure-impulse diagram with multiple failure modes of one-way reinforced concrete slab under blast loading using SDOF method [J]. Journal of Central South University of Technology, 2013, 20(2):510-519.

[11] 李忠獻，師燕超，史祥生. 爆炸載荷作用下鋼筋混凝土板破壞評定方法[J]. 建筑結構學報, 2009, 30(6):61-66.

LI Zhong-xian, SHI Yan-chao, SHI Xiang-sheng. Damage analysis and assessment of RC slabs under blast load [J]. Journal of Building Structures, 2009, 30(6):61-66.

[12] Huang X, Li J C, Ma G W. Damage analysis of RC column/beam subject to blast load [C]//Proceedings of the 8th International Conference on Shock and Impact Loads on Structures. Adelaide:2009, 311-320.

[13] Shi Y C,Hao H, Li Z X. Numerical derivation of pressure-impulse diagrams for prediction of RC column damage to blast loads [J]. International Journal of Impact Engineering, 2008, 35(11): 1213-1227.

[14] Wu C, Sheikh H. Simulation of pressure impulse diagrams for foam protected RC members[C]//Proceedings of the 22nd Australasian Conference on the Mechanics of Structures and Materials, ACMSM 2012:787-792.

[15] Mutalib A A, Hao H. Development of P-I diagrams for FRP strengthened RC columns [J]. International Journal of Impact Engineering, 2011, 38(5): 290-304.

[16] Huang X, Ma G W, Li J C. Damage assessment of reinforced concrete structural elements subjected to blast load [J]. International Journal of Protective Structures, 2010(1): 103-124.

Simplified calculation method for pressure-impulse curve of a structure under blast load

CHEN Jun-jie1, GAO Kang-hua1, SUN Ao2

(1. State Key Laboratory for Disaster Prevention and Mitigation of Explosion and Impact, PLA University of Science and Technology, Nanjing 210007, China;2. The Third Engineer Scientific Research Institute of General Staff, Luoyang 471023, China)

Pressure-impulse (P-I) curves can be used to quickly assess damage effect of a structure under blast load. Based on motion equations of an equivalent single-DOF system and structural deformation’s ideal elaso-plastic model, damping effect was considered with the traditional energy method, and damping energy dissipation was calculated by using the image method. The asymptote equations of quasi-static region and impulse region of a P-I curve were obtained, and the fitting formulas for dynamic region of a P-I curve were obtained through a large amount of calculation. The calculation results with the proposed simplified calculation formulas agreed well with P-I curves obtained using structural analysis of Newark method. The rationality of the proposed method was verified. The calculation results showed that the values of impulse asymptote and quasi-static asymptote decrease with increase in ductility ratio; the values of impulse asymptote and quasi-static asymptote increase with increase in damping ratio, and the damping ratio has an obvious effect on impulse asymptote.

pressure-impulse curve; single-DOF system; elastic ideal elaso-plastic model; damping effect; damage assessment

10.13465/j.cnki.jvs.2016.13.036

國家自然科學基金青年基金項目(51308542);國家自然科學創新研究群體科學基金(51021001)

2015-07-06修改稿收到日期：2015-12-15

陳俊杰 男，碩士生，1991年生

高康華 男，博士，1983年生

O322;TU312.1

A