相位調諧對行星齒輪系統輻射噪聲影響的研究

戴　麟, 朱如鵬, 鮑和云, 張霖霖, 曹　鑫

(南京航空航天大學 機電學院，南京　210016)

相位調諧對行星齒輪系統輻射噪聲影響的研究

戴麟, 朱如鵬, 鮑和云, 張霖霖, 曹鑫

(南京航空航天大學 機電學院，南京210016)

考慮齒輪嚙合相位因素得到相位調諧前后各傳動齒輪齒數配比，應用集中質量法建立行星齒輪傳動系統的動力學模型，計算齒輪箱軸承支撐動載荷。建立單級行星齒輪傳動系統齒輪箱的三維幾何模型，將動載荷作為激勵施加于齒輪箱軸承支撐處，通過有限元法計算得齒輪箱的模態頻率和振動響應。在Virtual.lab中建立齒輪箱的邊界元模型并導入齒輪箱振動位移響應作為邊界條件，應用直接邊界元法計算得到相位調諧前后齒輪箱輻射噪聲。對比試驗結果表明，相位調諧方法可有效地降低噪聲，證明相位調諧方法降噪的可行性。

齒輪箱；有限元法；直接邊界元法；相位調諧；噪聲

齒輪傳動是各種機械裝備中應用最廣的動力和運動傳遞裝置。齒輪傳動系統在運轉過程中，由于同時嚙合齒輪對數的變化、輪齒的受載變形、齒輪誤差等原因，導致嚙合過程中輪齒動態嚙合力的產生，齒輪振動經過軸傳遞到軸承座，再由軸承座傳到齒輪箱，激起齒輪箱振動并形成輻射噪聲。

目前，以減振降噪為主要目的的行星齒輪動力學引起了廣泛關注。行星齒輪傳動的減振方法主要有兩種：參數修改方法(如行星傳動基本參數的選擇、系統剛度及慣性參數的調整、以及輪齒修形等)和結構修改方法(如中心構件浮動、附加均載機構等)。相位調諧方法是參數修改方法中的一種，即通過改變基本參數實現嚙頻激勵相位的調整，使得行星齒輪的多重嚙合之間具有特定的相位關系，從而減小中心構件所受激勵，這樣便可以減小振動響應和消除某階共振，以達到減振降噪的效果。

相位調諧現象最先是由Schlegel等[1]發現并研究的。Parker[2]通過嚙合力分析對相位調諧開展了深入的研究。王世宇[3]通過直齒行星系統的彎扭耦合動力學模型對相位調諧進行仿真研究，闡述了相位調諧因子與構件運動特性之間的關系。Kato等[4]采用FEM/BEM法對單級齒輪箱的振動和噪聲輻射進行了分析，并與試驗結果作出了對比。張金梅等[5]以單級人字齒輪減速器為研究對象，討論了負載、誤差等對減速器輻射噪聲的影響。周建星等[6-8]以人字齒輪減速器為研究對象，提出了減速器輻射噪聲分析方法，并以同樣的方法研究了轉速與負載對減速器振動噪聲的影響，為減速器的減振降噪設計提供了理論基礎。

本文首先推導了傳動系統中各嚙合副之間的嚙合相位系數，論述相位調諧因子與構件運動特性之間的關系；其次應用集中質量法建立了系統動力學模型，求解齒輪箱軸承支撐動載荷；然后建立齒輪箱有限元、邊界元模型，將動載荷施加于齒輪箱軸承支撐處，通過有限元法計算齒輪箱的動態響應，并將其作為邊界條件施加于齒輪箱邊界元模型，應用直接邊界元法計算齒輪箱的輻射噪聲；最后通過試驗測得相位調諧與原始組不同情況下齒輪箱輻射噪聲，經過對比分析驗證了相位調諧方法對降噪的可行性。

1　相位調諧原理

以行星架為參考對象，假設輪齒轉過一個齒距角的時間為嚙合周期T，即

(1)

式中：Zs為太陽輪齒數，ωs，ωc分別為太陽輪，行星架的轉動角速度，則第n個太陽輪-行星輪嚙合副和第1個太陽輪-行星輪嚙合副之間的時間差為Δtsn，即

Δtsn=λsnT

(2)

式中：λsn表示第n個太陽輪-行星輪嚙合副和第1個太陽輪-行星輪嚙合副之間的嚙合相位系數。

假設第n個行星輪與第1個行星輪之間的夾角為φn,太陽輪相對行星架旋轉φn時，行星輪n運動到行星輪1的位置，所需要的時間為t，即

(3)

式中：N表示行星輪個數。

由齒輪之間的傳動關系可知，

Δtsn+PT=t

(4)

式中：P表示任意整數，聯立式(1)～(4)可得嚙合相位系數λsn，即

(5)

式中：dec表示取小數部分。

同理可推導出嚙合相位系數λrn，即

(6)

式中：λrn表示第n個內齒圈-行星輪嚙合副與第1個內齒圈-行星輪嚙合副之間的嚙合相位系數，Zr為內齒圈齒數。相位調諧規律[9]如表1所示。

表1中K=mod(lzs/N)，l表示諧波階數，N表示行星輪個數。

由表1可知，當相位調諧因子不為0時，系統中心構件的平移振動會得到一定的激起，平移振動較大。當相位調諧因子為0時，系統中心構件的平移振動才會得到抑制，平移振動才會降低。

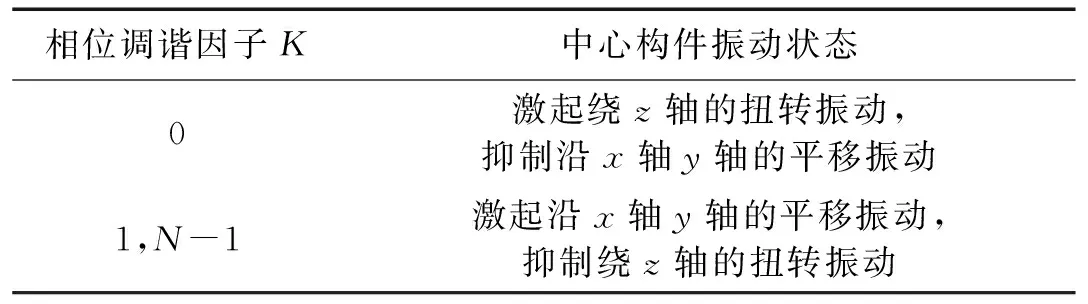
表1　相位調諧規律

2　齒輪箱軸承支撐動載荷計算

2.1計入嚙合相位的時變嚙合剛度分析

本文嚙頻激勵主要考慮輪齒的時變嚙合剛度激勵，故本文將嚙合相位系數代入齒輪副時變嚙合剛度當中。假設ks1表示太陽輪與第1個行星輪之間的嚙合剛度，kr1表示第1個行星輪與內齒圈之間的嚙合剛度，則太陽輪與第n個行星輪之間的嚙合剛度ksn(t)為

ksn(t)=ks1(t-λsnT)

(7)

第n個行星輪與內齒圈之間的嚙合剛度krn(t)為

krn(t)=kr1(t-λrnT)

(8)

太陽輪-行星輪與行星輪-內齒圈時變嚙合剛度如圖1，2所示。

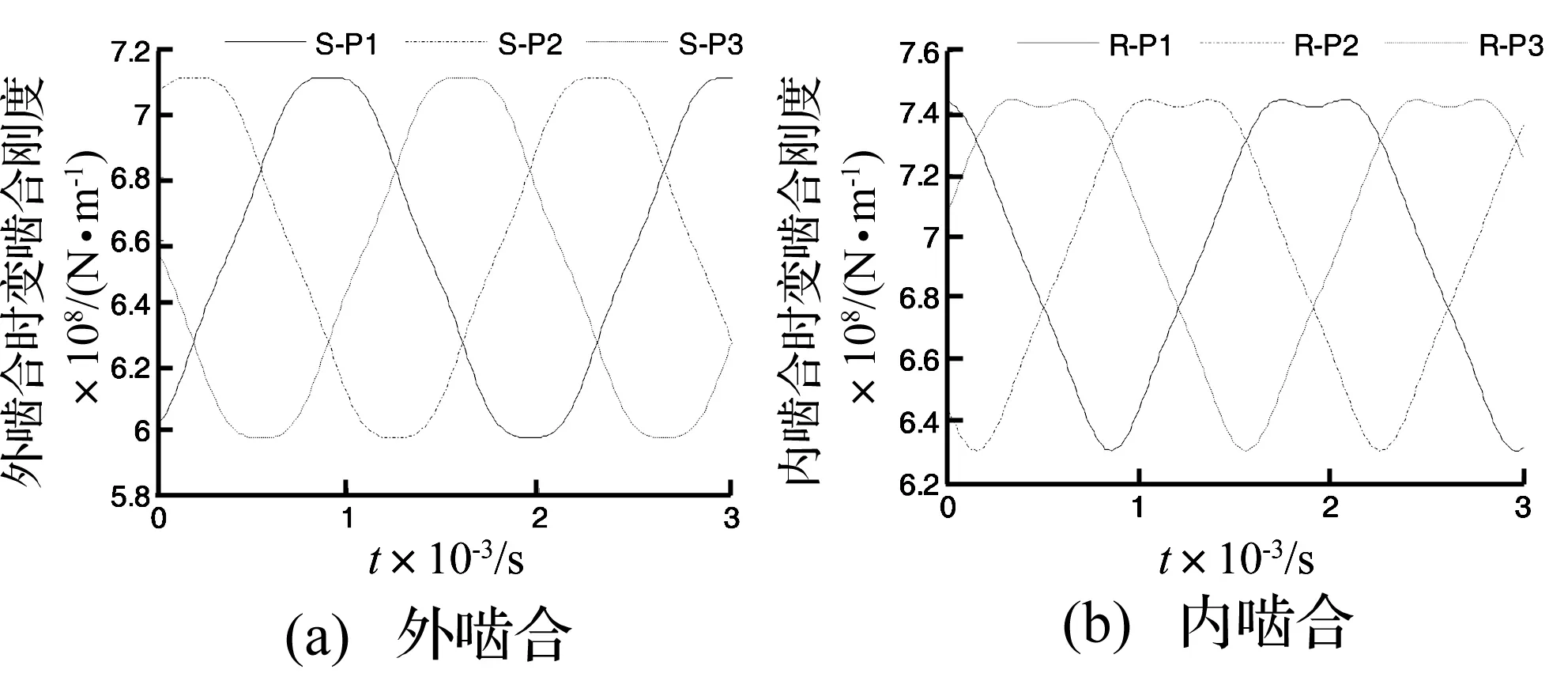
圖1　有相位差內、外嚙合副時變嚙合剛度Fig.1 Meshing stiffness with phase difference

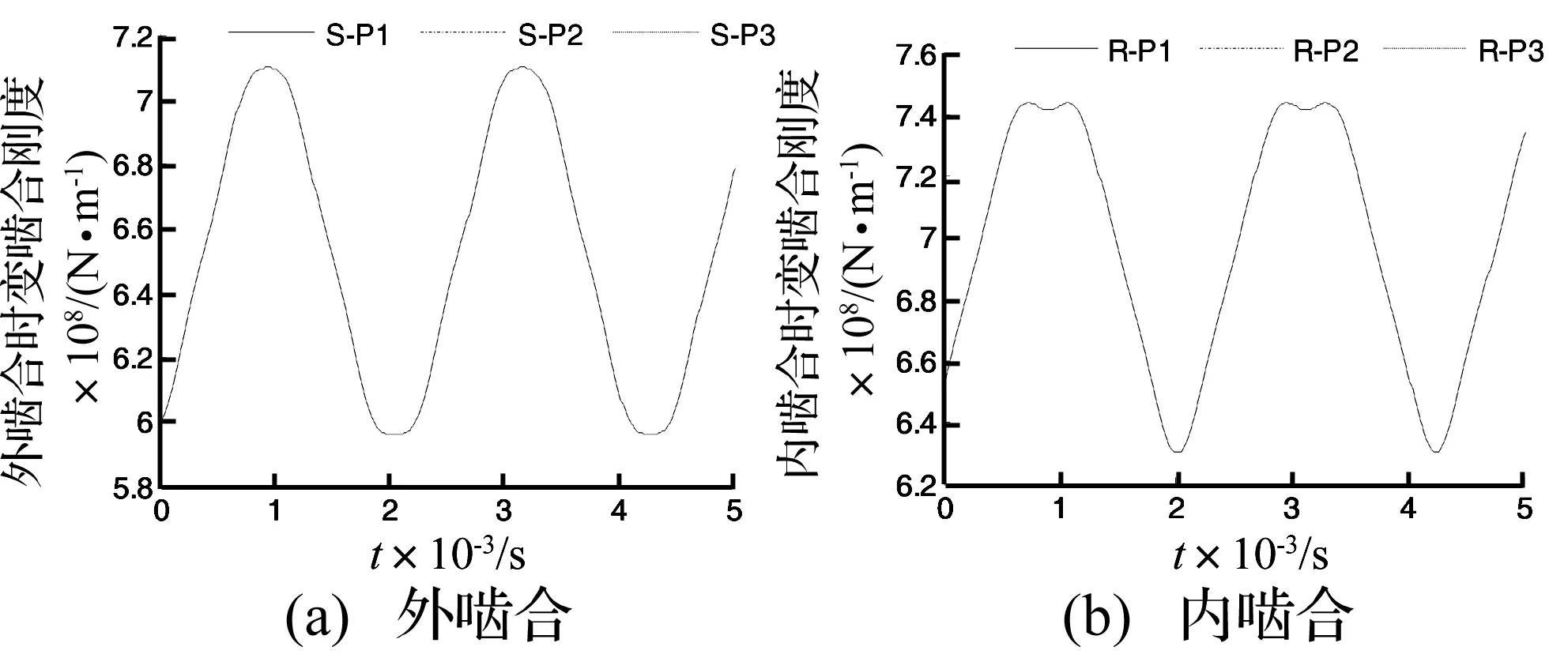
圖2　無相位差內、外嚙合副時變嚙合剛度Fig.2 Meshing stiffness without phase difference

由圖1可知，當嚙合副之間有嚙合相位差時，嚙合副時變嚙合剛度之間存在相位差。由圖2可知，相位調諧后嚙合副之間相位差為0°，嚙合副之間沒有相位差，故嚙合副嚙合剛度之間沒有相位差。

2.2系統動力學模型

應用集中質量法建立單級行星齒輪傳動系統平移-扭轉耦合動力學模型[10]如圖3所示。

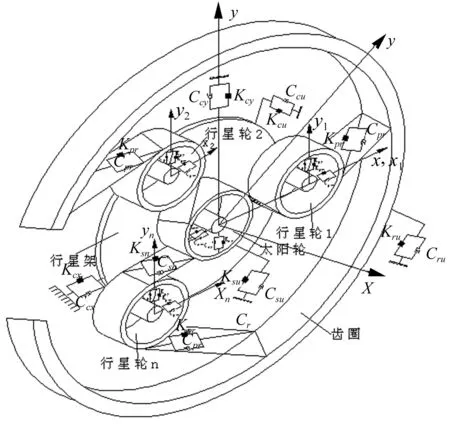
圖3　系統動力學模型Fig.3 The dynamic model of the system

本文考慮了輸入軸扭轉位移uD，太陽輪水平位移Xs、豎直位移Ys和扭轉位移us，行星輪水平位移Xpn、豎直位移Ypn和扭轉位移upn，內齒圈水平位移Xr、豎直位移Yr，行星架水平位移Xc、豎直位移Yc和扭轉位移uc，輸出軸扭轉位移uL。綜合考慮齒輪嚙合誤差、計入嚙合相位的時變嚙合剛度等激勵建立系統動力學模型。

系統中各構件位置關系如圖4所示。

太陽輪中心和行星輪中心在嚙合線上的相對位移δsn為

δsn=(xn-xs)sin(φn-αspt)+

(ys-yn)cos(φn-αspt)+us+un-esn

(9)

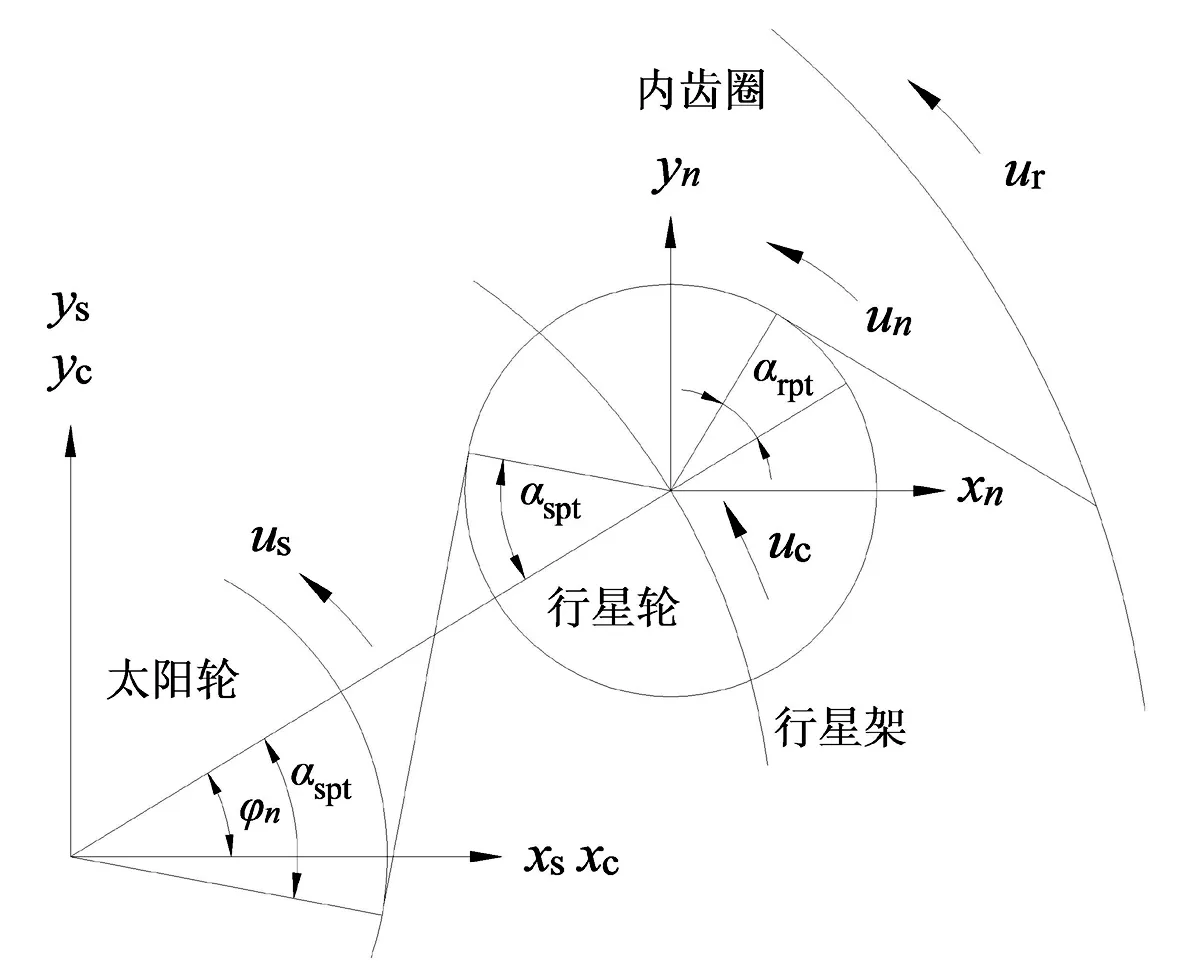
圖4　系統構件相對位置Fig.4 Feature relative position

行星輪中心和內齒圈中心在嚙合線上的相對位移δrn

δrn=(xn-xr)sin(φn+αrpt)+

(yr-yn)cos(φn+αrpt)-un+ur-ern

(10)

行星輪中心與行星架中心在xc，yc和uc方向上的相對位移δcnx，δcny，δcnu為

(11)

行星輪中心與行星架中心在xn，yn方向上的相對位移δxn，δyn

(12)

式中φn為行星輪n的位置角；αspt為太陽輪-行星輪嚙合角；αrpt為行星輪-內齒圈嚙合角；esn為第n個太陽輪-行星輪嚙合線上的綜合嚙合誤差；ern為第n個行星輪-內齒圈嚙合線上的綜合嚙合誤差。

根據牛頓第二運動定律得系統運動微分方程有：

(13)

式中：u，x，y分別表示扭轉自由度、水平方向平移自由度、豎直方向平移自由度；TD、TL表示輸入、輸出扭矩；I、ω，βb表示轉動慣量、轉動角速度與螺旋角；csu、ksu表示輸入軸和太陽輪之間的扭轉阻尼和扭轉剛度；ksx、csx分別表示太陽輪的橫向支撐剛度和橫向支撐阻尼；ksn、csn分別表示太陽輪與行星輪之間的嚙合剛度與嚙合阻尼；ksy、csy分別表示太陽輪的縱向支撐剛度和縱向支撐阻尼 ；kpn、cpn分別表示行星輪與行星架之間的支撐剛度和支撐阻尼；krn、crn分別表示行星輪與內齒圈之間的嚙合剛度與嚙合阻尼；krx、crx分別表示內齒圈的橫向支撐剛度與橫向支撐阻尼；kry、cry分別表示內齒圈的縱向支撐剛度和縱向支撐阻尼；kcx、ccx分別表示行星架的橫向支撐剛度與橫向支撐阻尼；kcy、ccy分別表示行星架的縱向支撐剛度與縱向支撐阻尼；kcu、ccu分別表示行星架與輸出軸之間的扭轉剛度和扭轉阻尼。

由于相位調諧后各構件齒數發生改變，系統的嚙合頻率與原始組不同，為了方便對比分析，調整相位調諧組的轉速使得相位調諧后系統的嚙合頻率與原始組嚙合頻率相同，系統參數如表2所示。

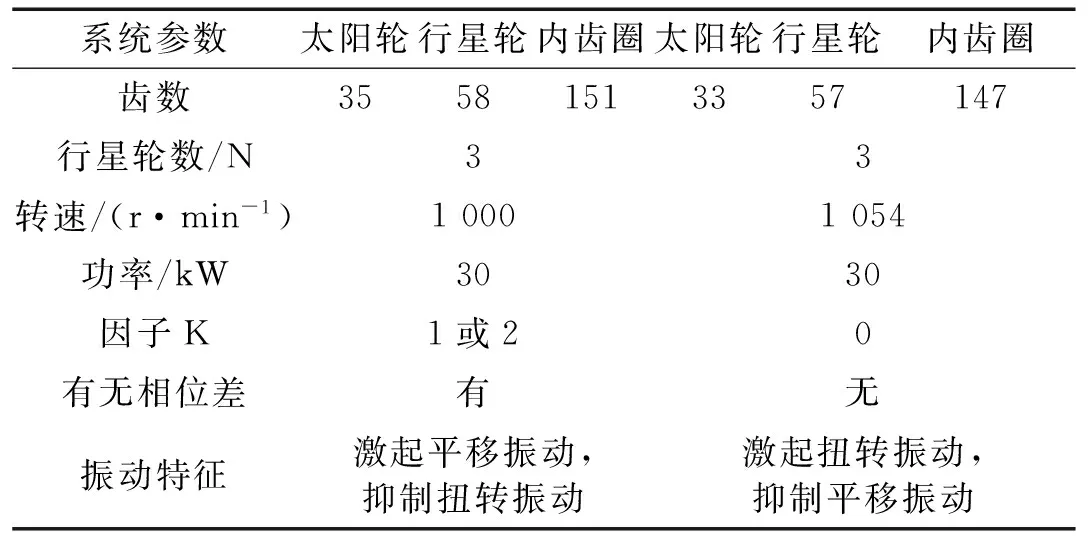
表2　系統參數

2.3動載荷計算

系統運動微分方程可以整理成如下矩陣形式。

(14)

式中:M為質量矩陣；Cb為支撐阻尼矩陣；Cm為嚙合阻尼矩陣；Kb為支撐剛度矩陣；Km為嚙合剛度矩陣；Tk為誤差和計入嚙合相位的嚙合剛度引起的激振列陣；Tc為誤差和嚙合阻尼引起的激振列陣；T為外激勵列陣；q為廣義坐標列陣。應用傅里葉解法[11]求解箱體軸承支撐動載荷如圖5～7所示。

由圖5，6可知，嚙合相位使嚙頻激勵相位發生調整，從而各構件動力學特性發生改變。原始參數下輪齒嚙合存在相位差，平移振動較大，齒輪箱受到的動載荷較大；相位調諧為0°后輪齒嚙合相位差為零，平移振動較小，齒輪箱受到的動載荷較小；由圖7可知，相位調諧后動載荷頻域成分與之前相比也有所降低。箱體動載荷變化規律與表1規律相符。

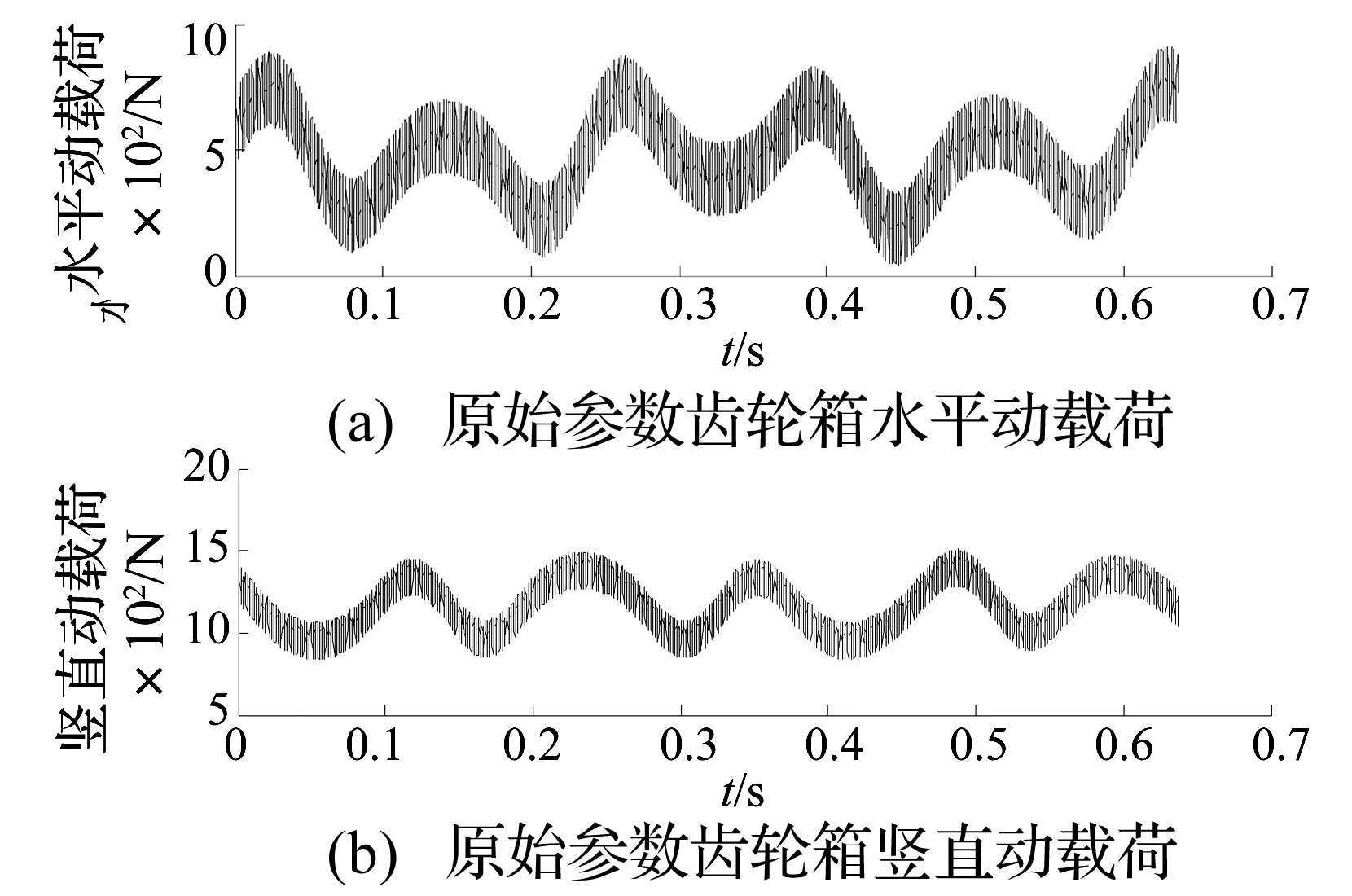
圖5　原始參數齒輪箱動載荷時域圖Fig.5 Original dynamic load of the gearbox in time domain

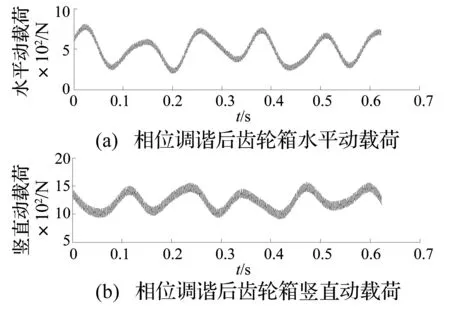
圖6　相位調諧后齒輪箱動載荷時域圖Fig.6 The dynamic load of the gearbox after phase adjustment in time domain

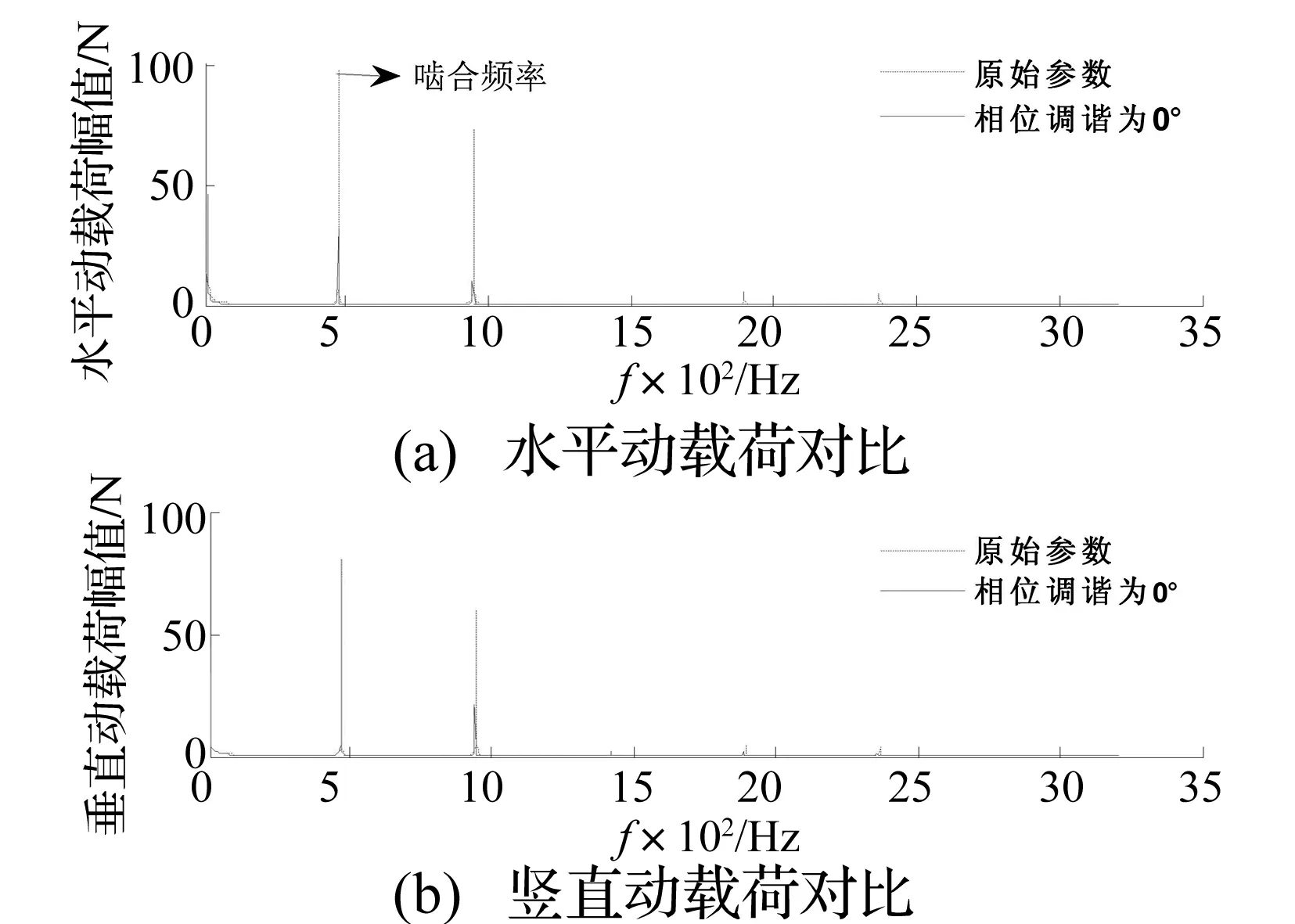
圖7　齒輪箱動載荷頻域對比Fig.7 The comparison of the dynamic load in frequency domain

3　齒輪箱體動響應計算

借助于有限元軟件Abaqus建立齒輪箱體的有限元模型如圖8所示，對其劃分網格、定義材料等屬性之后，在齒輪箱底部施加固定約束，計算齒輪箱模態頻率。在齒輪箱軸承孔處建立局部坐標，坐標原點位于孔的中心點，并在Abaqus中建立中心點與孔的耦合關系，將動載荷施加于中心點。采用瞬時模態動態分析法計算得原始組與相位調諧組齒輪箱體表面部分節點位移動響應如圖9，10所示。

圖8　齒輪箱體有限元模型Fig.8 The FEM model of the gearbox

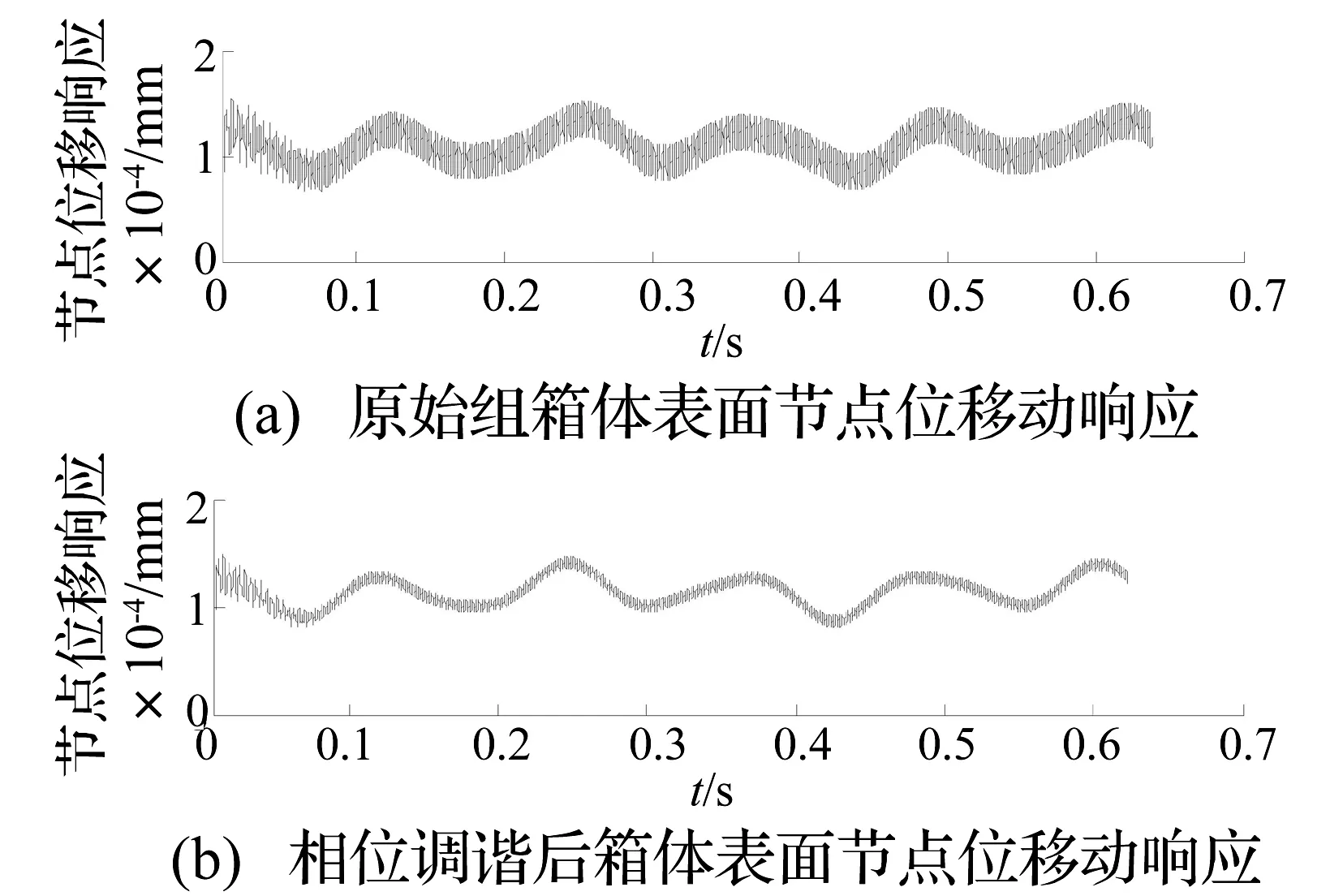
圖9　箱體表面節點位移響應時域圖Fig.9 The node dynamic response of the gearbox in time domain

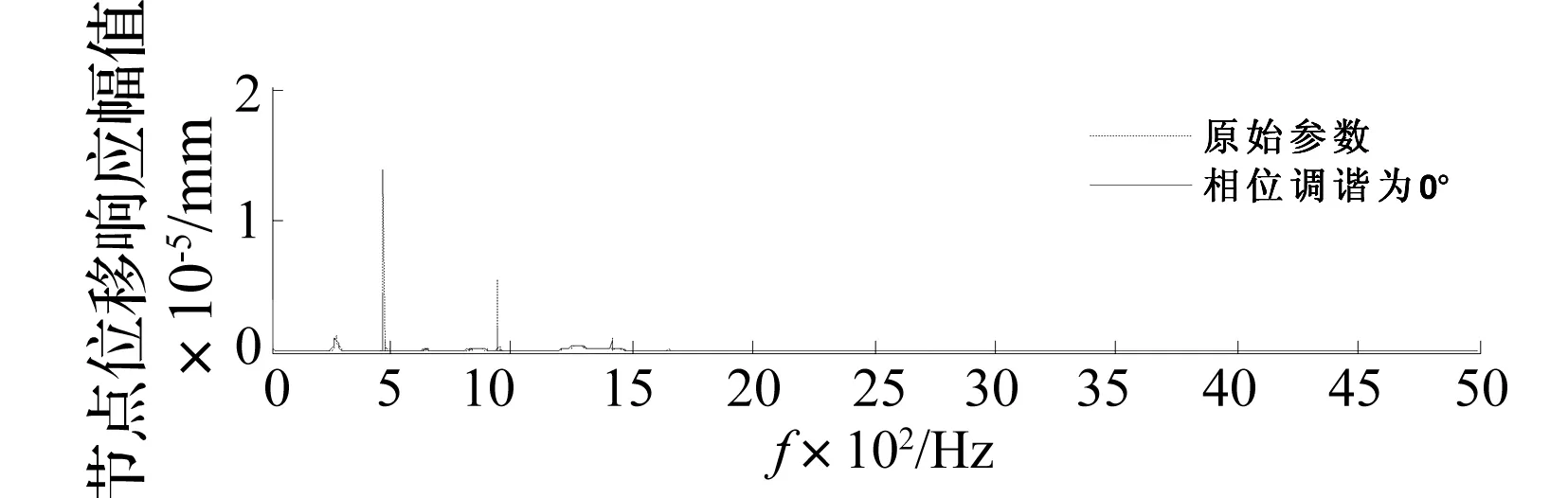
圖10　箱體表面節點位移動響應頻域對比Fig.10 The comparison of the node dynamic response of the gearbox in frequency domain

由圖10可知，相位調諧后齒輪箱表面節點動響應基頻及倍頻所占比例與原始組相比都有所降低。可知，齒輪箱動載荷基頻及倍頻激勵成分的下降使得箱體表面節點動響應中基頻及倍頻成分降低。

4　齒輪箱體輻射噪聲計算

行星齒輪系統的聲場是一個非封閉空間聲場，只應用有限元方法很難求解。本文在Virtual.lab中建立齒輪箱封閉的邊界元模型及外聲場模型如圖11所示。

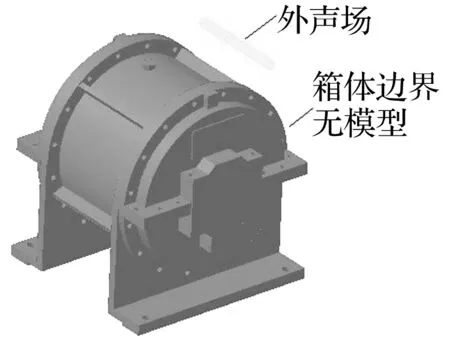
圖11　齒輪箱體邊界元及外聲場模型Fig.11 The BEM model of the gearbox and outer sound field

由于箱體有限元網格為實體網格，邊界元模型網格為面網格，這兩個網格不匹配，所以需要設置這兩個網格之間的映射關系。設置距離邊界元模型上某節點100 mm的范圍內，從有限元網格節點上最多找4個最近的節點對應目標網格的一個點。如圖12所示，如果原網格上的4個點對應目標網格上的一個點A，這4個點與目標網格點A的距離為di(i=1,2,3,4)，這4個點上的振動速度為vi(i=1,2,3,4)，那么目標點A的振動速度v為

(15)

圖12　數據轉移示意圖Fig.12 Schematic diagram of data transfer

圖中1，2，3，4為有限元網格上的節點，A為邊界元網格上的節點。

將有限元求解得到的節點位移動響應作為邊界條件導入齒輪箱體邊界元模型中，應用直接邊界元法計算得箱體表面噪聲云圖及外場點噪聲頻譜曲線如圖13，14所示。

圖13　嚙頻處齒輪箱表面聲壓云圖Fig.13 The distribution of the noise radiation on the gearbox surface at the meshing frequency

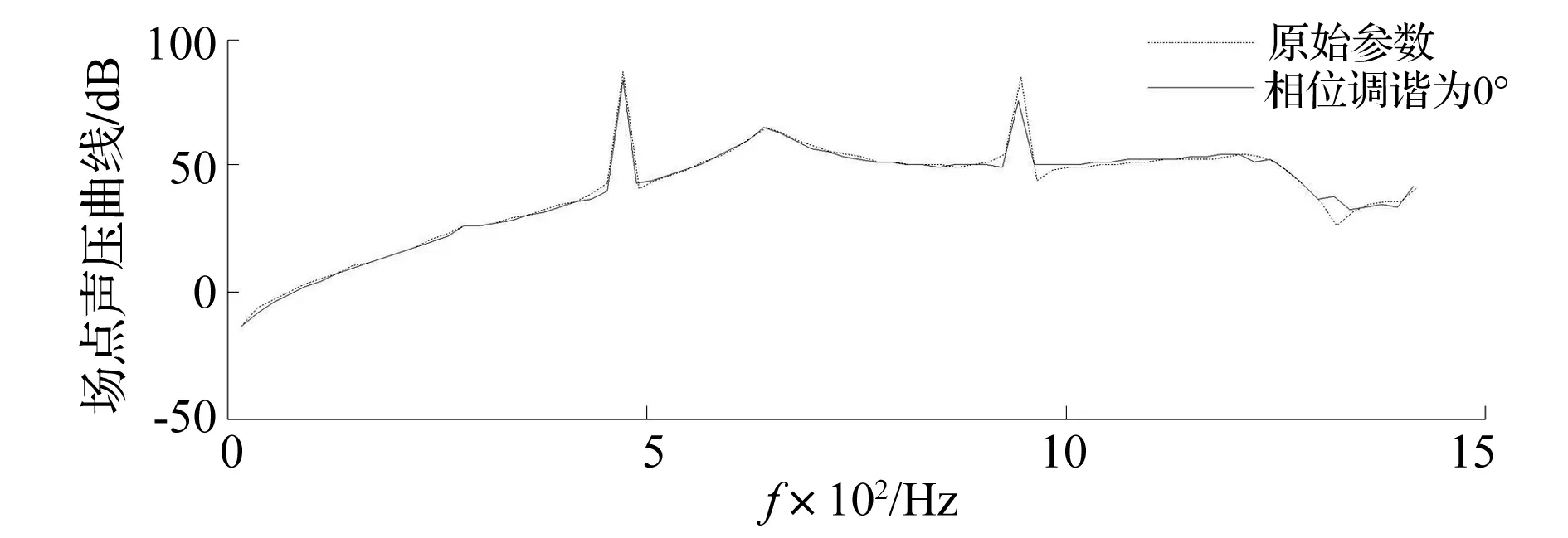
圖14　外聲場場點噪聲頻譜曲線Fig.14 The curve of the field point for noise

由圖13可知相位調諧后齒輪箱表面噪聲值有所下降，與原始組相比在基頻處齒輪箱表面噪聲在最大值處下降了1 dB；由圖14可知在計算頻率范圍內，場點噪聲在基頻及2倍頻處都達到峰值。原始參數下，場點噪聲值在基頻處達到86.91 dB，在2倍頻處達到85.21 dB。相位調諧后，場點噪聲值在基頻處達到84.03 dB，2倍頻處達到75.87 dB。在基頻處相位調諧之后場點噪聲值下降了2 dB左右，在2倍頻處噪聲值下降了9 dB左右。可知，相位調諧后，基頻及倍頻振動所占比例下降，使得傳遞到箱體上的振動降低，從而使得箱體輻射噪聲下降。

5　試驗研究

試驗需加工兩組參數齒輪，一組為原始組參數，一組為相位調諧后的參數，具體參數如表3所示。同樣為了使測量結果具有一定的可比性，兩組試驗的輸入轉速不同，原始組輸入轉速為1 000 r/min，相位調諧組輸入轉速改為1 054 r/min，這樣保證兩組試驗系統的基頻相同。

5.1試驗測試方案

試驗臺由控制柜、底座、潤滑油站、電機、單級人字齒行星齒輪傳動試驗件、磁粉制動器和隔音罩等組成如圖15，16所示。

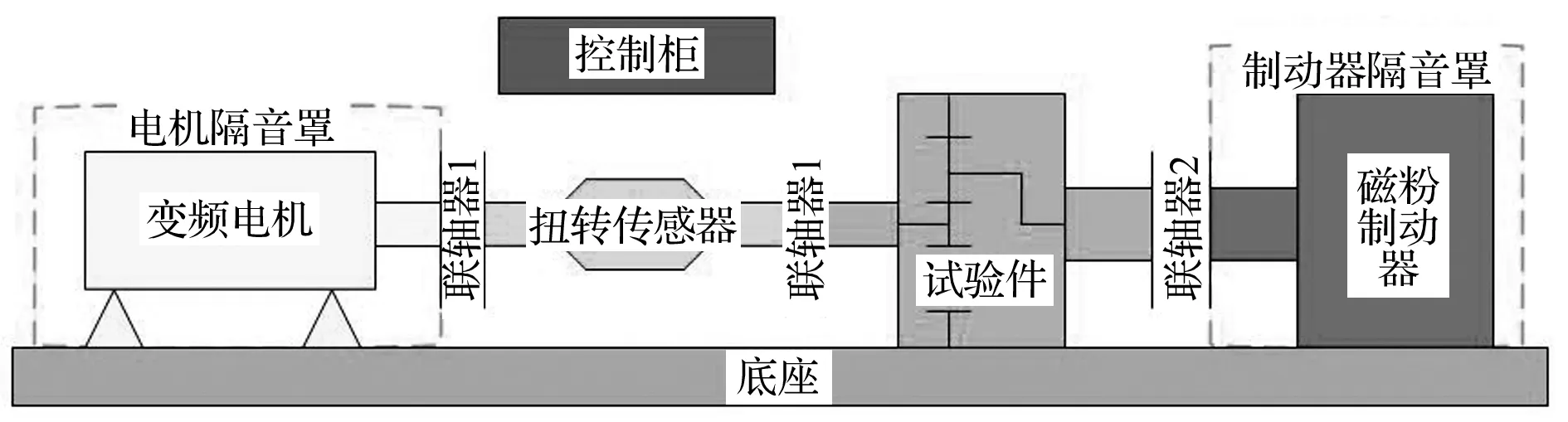
圖15　試驗裝置方案Fig.15 The scheme of the experiment

圖16　試驗測試現場Fig.16 The scene of the experiment

噪聲測試主要利用聲強探頭測量確定扭矩和穩定轉速下的噪聲分貝值。聲強探頭里含有兩個聲壓傳感器，通過德國M+P公司數據采集與分析系統中的Acoustic模塊可以測出箱體輻射聲壓級信號。通過測量原始組與相位調諧后齒輪箱輻射聲壓并作對比分析驗證相位調諧的降噪效果。

5.2試驗結果分析

在功率恒定為30 kW條件下，測得原始組與相位調諧組齒輪箱輻射噪聲如圖17所示。

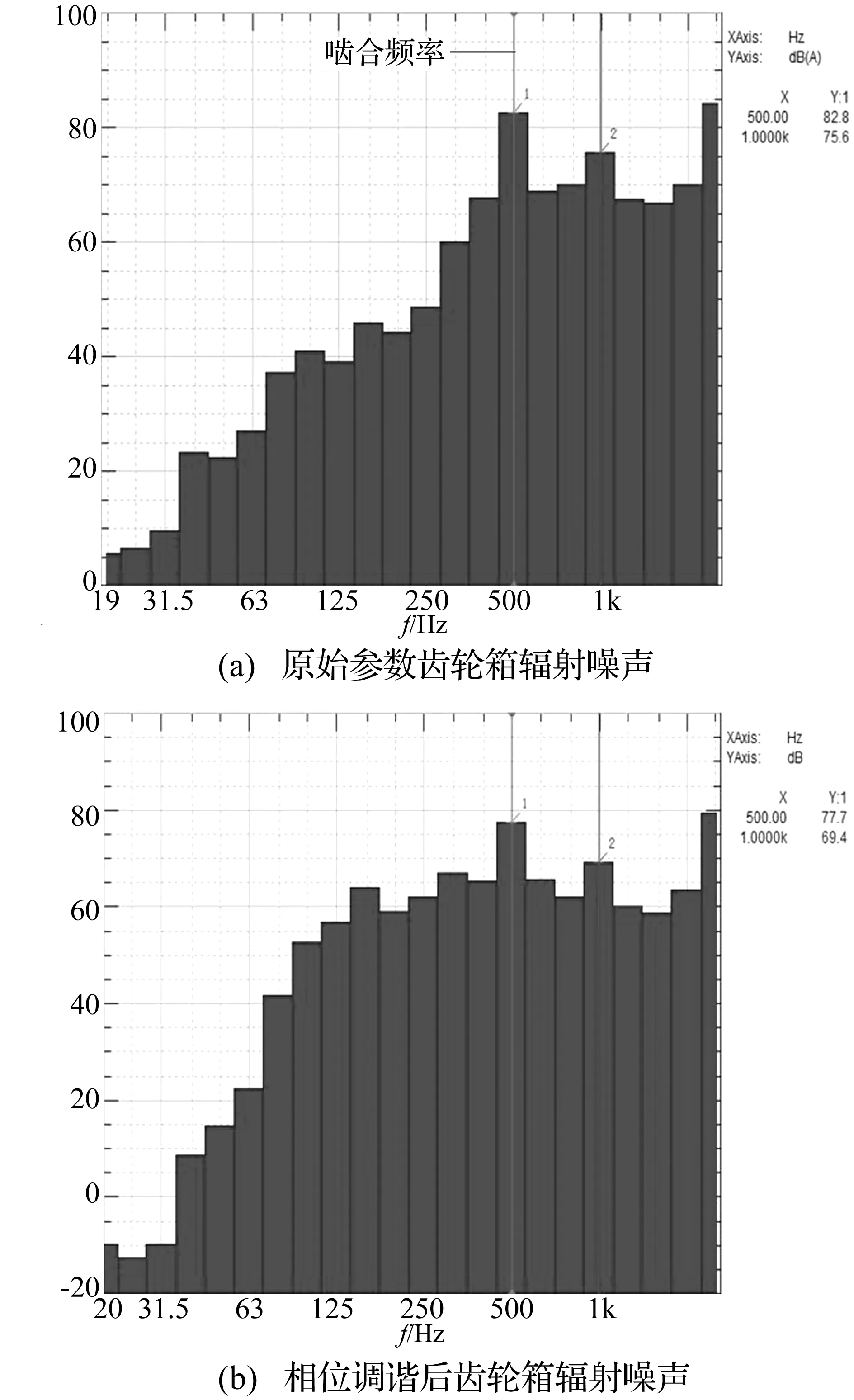
圖17　齒輪箱輻射噪聲試驗值Fig.17 The noise radiation of the gearbox by experiment

由圖17可知，齒輪箱輻射噪聲同樣在基頻與2倍頻達到峰值。原始組在基頻處箱體輻射噪聲值為82.8 dB，2倍頻處達到75.6 dB。相位調諧組測得在基頻處箱體輻射噪聲值為77.7 dB，2倍頻處噪聲值達到69.4 dB。與原始組相比，相位調諧后齒輪箱在基頻處的輻射噪聲值下降了5 dB左右，在2倍頻處輻射噪聲值下降了6 dB。由于理論計算中給予的誤差激勵值與實際裝配過程中的誤差值有所偏差等原因，使得理論計算結果與試驗測得結果有所差異，但理論仿真結果與試驗結果趨勢相同如表3所示。可知相位調諧后，輸入轉速比原始組還大，但是仿真結果與試驗測得數據表明相位調諧后箱體輻射噪聲比原始組小，更說明相位調諧方法對降噪的有效性。

6　結　論

(1) 相位調諧作為參數修改方法中的一種，在設計行星齒輪傳動系統時，通過合理選擇中心構件的齒數，使得行星齒輪的多重嚙合之間具有特定的相位關系，可以減小中心構件受到的激勵，其中嚙合相位對基頻及倍頻激勵降低作用較明顯。

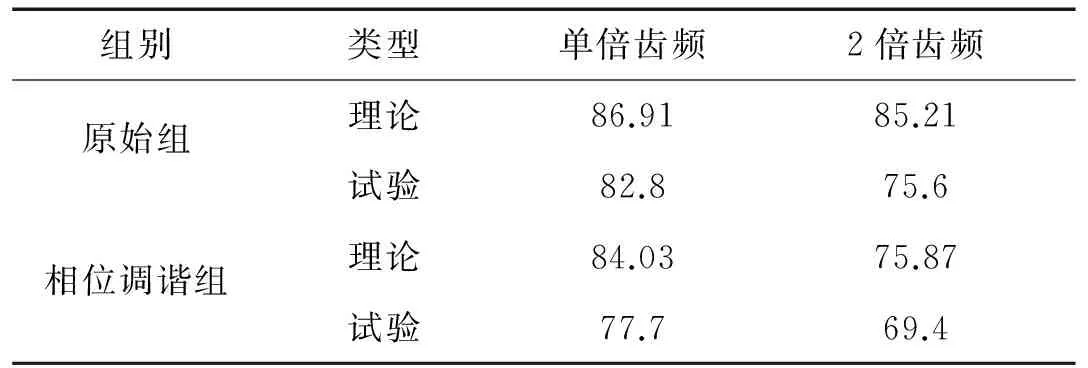
表3　場點輻射噪聲對比(dB)

(2) 相位調諧通過改變基本參數實現激勵之間相位的調整，使構件的平移振動得到一定的抑制，降低了傳遞到齒輪箱體上的動載荷，從而降低了齒輪箱體的振動和輻射噪聲,證明相位調諧方法對降噪的可行性。

[1] Schlegel R G,Mard K C. Transmission noise control-approaches in helicopter design[C]//New York: American Society of Mechanical Engineers Design Engineering Conference, 1967, ASME: 67-DE-58.

[2] Parker R G. A physical explanation of the effectiveness of planet phasing to suppress planetary gear vibration [J]. Journal of Sound and Vibration, 2000, 236(4): 561-573.

[3] 王世宇. 基于相位調諧的直齒行星齒輪傳動動力學理論與實驗研究[D]. 天津: 天津大學, 2005.

[4] Kato M, Inoue K, Shibata K, et al. Evaluation of sound power radiated by a gearbox[C]//Proc. Inter Gearing’94, 1994. 69-74.

[5] 張金梅,劉更,周建星,等. 人字齒輪減速器振動噪聲影響因素仿真分析研究[J]. 振動與沖擊,2014,33(11):161-167.

ZHANG Jin-mei, LIU Geng, ZHOU Jian-xing, et al. Simulation analysis of influencing factors on vibration and noise of a herringbone gear speed-reducer[J]. Journal of Vibration and Shock, 2014, 33 (11): 161-167.

[6] 周建星,孫文磊. 單極人字齒輪減速器振動噪聲分析方法研究[J]. 振動與沖擊, 2013, 33(9): 66-71.

ZHOU Jian-xing, SUN Wen-lei.Vibration and noise analysis of a herringbone gear transmission system[J]. Journal of Vibration and Shock, 2013, 33(9): 66-71.

[7] 周建星,劉更,馬尚君. 內激勵作用下齒輪箱動態響應與振動噪聲分析[J]. 振動與沖擊, 2011, 30(6): 234-238.

ZHOU Jian-xing, LIU Geng, MA Shang-jun. Vibration and noise analysis of the gear transmission system[J]．Journal of Vibration and Shock, 2011, 30(6): 234-238．

[8] 周建星,劉更,吳立言. 轉速與負載對減速器振動噪聲的影響研究[J]. 振動與沖擊, 2013, 32(8): 193-198.

ZHOU Jian-xing, LIU Geng, WU Li-yan. Effect of operating conditions on vibration and noise radiation of a gear reducer[J]. Journal of Vibration and Shock, 2013, 32 (8): 193-198.

[9] Kahraman A, Blankenship G W. Planet mesh phasing in epicyclic gear sets [C]//Newcastle, UK: Proceedings of International Gearing Conference, 1994: 99-104.

[10] 李發家,朱如鵬,鮑和云,等. 行星齒輪系統動力學特性分析及試驗研究[J]. 南京航空航天大學學報, 2013, 44(4):511-519.

LI Fa-jia, ZHU Ru-peng, BAO He-yun, et al.Dynamics characteristics and experiment research on planetary gear system[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 44(4): 511-519.

[11] 鮑和云,朱如鵬. 兩級星型齒輪傳動動態均載特性分析[J]. 航空動力學報, 2005, 20(6): 937-943.

BAO He-yun, ZHU Ru-peng.Analysis of dynamic load sharing in a 2-Stage planet gear train[J]. Journal of Aerospace Power, 2005, 20(6): 937-943.

Effects of phase adjustment on noise radiation in a planetary gear transmission system

DAI Lin, ZHU Ru-peng, BAO He-yun, ZHANG Lin-lin, CAO Xin

(College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

The number of gears’ teeth was computed considering phase adjustment in a single-level planetary gear transmission system. The dynamic model of the planetary gear transmission system was set up by using the lumped mass method. The dynamic load of the bearing of the system’s gearbox was taken as the excitation and the 3-D geometric model of the gearbox was built. Modal frequencies and vibration responses of the gearbox were computed with the finite element method. By using the method of the boundary element method (BEM) and the software Virtual.lab, the acoustic radiation pressure levels of the gearbox before and after phase adjustment were computed using a 3-D BEM model and boundary conditions imported with the results of vibration responses. The calculation results were compared with test data. It was shown that the phase adjustment method can effectively reduce noise radiation and its feasibility is verified.

gearbox; finite element method; direct boundary element method; phase adjustment; acoustic pressure

10.13465/j.cnki.jvs.2016.13.009

中央高校基本科研業務費專項資金資助(NZ2014201);國家自然科學基金資助(51305196)

2015-03-18修改稿收到日期：2015-07-07

戴麟 男，碩士生，1990年2月生

朱如鵬 男，博士,教授，1959年9月生

TH113

A