脫膠圓襯砌及其邊緣直裂紋對出平面波的散射

南景富, 趙春香, 齊　輝, 楊在林, 高國付, 于麗艷, 趙繼濤

(1.黑龍江科技大學 理學院,哈爾濱　150022； 2.哈爾濱工程大學 航天與建筑工程學院,哈爾濱　150001)

脫膠圓襯砌及其邊緣直裂紋對出平面波的散射

南景富1, 趙春香1, 齊輝2, 楊在林2, 高國付1, 于麗艷1, 趙繼濤1

(1.黑龍江科技大學 理學院,哈爾濱150022； 2.哈爾濱工程大學 航天與建筑工程學院,哈爾濱150001)

通過數學物理方法中的Green函數法研究了界面上含有上半圓形脫膠圓形襯砌及其邊緣界面直線型裂紋的均勻雙相介質全空間對出平面動力的響應。首先，給出了在含有半圓形凸起的圓形襯砌的下半空間和含半圓形凹陷的上半空間在水平分界面上任意一點加載出平面線源波動時在各自區域產生的位移場；再者，給出出平面波任意角度入射時的入射波、反射波、折射波和散射波函數；其次，采用裂紋"切割"方法構造直線型裂紋,并應用邊界條件對上下半空間在界面處實施“契合”，建立起問題的定解方程組；最后做為算例討論分析了裂紋尖端動應力強度因子的數值結果。

動應力強度因子(DSIF);半圓形脫膠;直線型裂紋;Green函數；出平面動力響應

隨著新材料科學的迅速發展，力學界人士對材料中缺陷的受力響應問題一直有很高的熱情，尤以對材料中的斷裂問題有很大的興趣。20世紀50年代末,Williams分析了全空間均勻雙相介質材料界面裂紋靜力問題, 在20世紀 90 年代劉殿魁等研究了界面裂紋尖端動應力強度因子在數值解基礎上的影響因素，汪越勝等計算了圓形邊界由于局部脫膠形成的曲線裂紋結構的裂紋尖端動應力強度因子的解析解及數值解。

本文采用數學物理方法中的 Green 函數法研究了水平界面上含有上半圓形脫膠襯砌及其邊緣界面直線型裂紋的全空間雙相均勻材料在承受任意角度入射的出平面波時產生的應力場和位移場,并推導了計算裂紋尖端動應力強度因子的函數方程。并以此問題的紋尖端動應力強度為算例進行了數值求解，討論了本力學模型的幾何參數、物理參數以及入射波數對動應力強度因子的影響。

1　所研究問題的力學模型

圖1(a)表示的是本問題的力學模型，即在界面上含有半圓形脫膠的圓形襯砌及其邊緣界面裂紋的全空間。將模型沿著界面S分成上下兩個半空間，上半部分為一含有半圓性凹陷的半空間，如圖1(b)所示；下半部分為一含有半圓形凸起圓形襯砌的半空間，如圖1(c)所示。

圖1　問題的力學模型Fig.1 The mechanics model of problem

2　線源波動載荷引起的位移函數

當在圖1(b)所示的上半空間水平邊界的任意一點加載一與時間協和的線源波動荷載時，上半空間的位移場通過Green函數法可表示為[5-11]

(1)

當在圖1(c)所示所示的下半空間水平邊界的任意一點加載一與時間協和的線源波動荷載時，下半空間的襯砌內位移場和下半空間其余部分位移場可分別表示為

W(st)=W′(st)+W″(st)=

(2)

(3)

式中，Am,Bm,Cm，Qm為待求常數，由邊界條件決定。W0為波的最大幅值。W(i)為入射波。W(s)為散射波。

(4)

3　問題的求解

圖2表示的是在本問題的力學模型空間中， 出平面波的以任意角度α0入射時的模型。

其中的入射波W(i)、反射波W(r)、和折射波W(f)的波場可表示為

(5)

(6)

(7)

式中,α0為波的入射角,α4為波的折射角

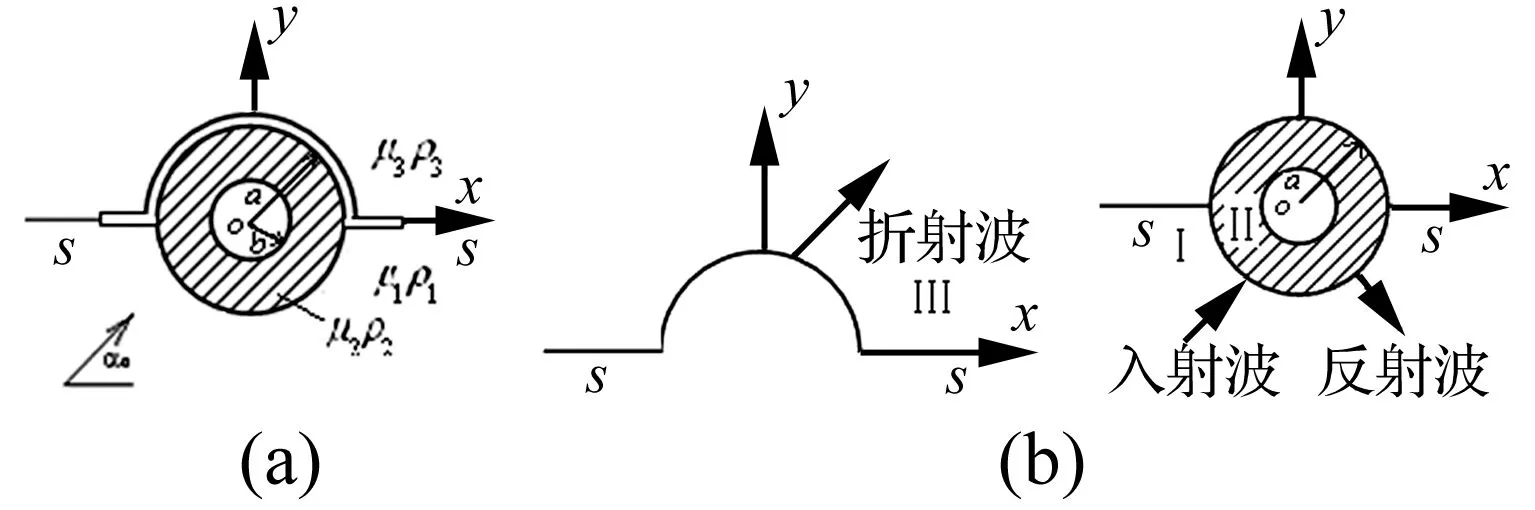
圖2　出平面波入射模型Fig.2 The model of the incidence of anti-plane-wave

同時采用與前面求解線源波動載荷引起的位移函數相同的方法，可以求得上下半空間中的散射波。

在下半空間的分界面s上，總的位移場和應力場可計算為

(8)

在上半空間的分界面s上，總的位移場和應力場可以計算為

(9)

圖3　模型接合示意圖Fig.3 Forming bi-media material

(10)

(11)

式中，a為襯砌的外半徑，c為裂紋的長度。

動應力強度因子(DSIF)的表達式為

式中，H表示裂紋尖端到原點O的距離。

f(G1+G2)=[f][G]=

通過上面關系式，可使kⅢ直接包含在定解積分方程組中。

無量綱的DSIF表達式為

(12)

特征參數Q在本問題中可表達為

τ0為入射波W(i)沿α0方向產生的應力最大值，表達式為

4　數值計算結果分析

(a) α0=90°,μ*1=1.0,μ*2=1.0,k*2=1.0,c/a=0.5(b) α0=90°,μ*1=1.0,μ*2=1.0,k*2=0.5,c/a=0.5(c) α0=90°,μ*1=1.0,μ*2=1.0,k*2=2.0,c/a=0.5圖4 出平面波α0=90°時,k*1不同時,DSIF隨k1a的變化Fig.4ThevariationofDSIFvs.k1aimpactedbyanti-planewaveverticallywhileα0=90°andk*1isdifferent

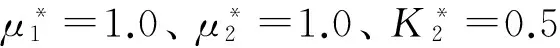
(4) 圖7給出了出平面波入射時，DSIF隨α0的變化情況。由圖可見，當k1a位于低頻段，α0為100度左右時，DSIF出現最大值；當k1a=0.1時，為準靜態，DSIF隨入射角的變化出現“雙峰”，并呈現近似90°度位置左右對稱。

(a) α0=90°,μ*1=1.0,μ*2=1.0,k*1=1.0,c/a=0.5(b) α0=90°,μ*1=1.0,μ*2=1.0,k*1=0.5,c/a=0.5(c) α0=90°,μ*1=1.0,μ*2=1.0,k*1=2.0,c/a=0.5圖5 出平面波α0=90°時,k*2不同時,DSIF隨k1a的變化Fig.5ThevariationofDSIFvs.k1aimpactedbyanti-planewaveverticallywhileα0=90°andk*2isdifferent

(a) α0=90°,μ*1=1.0,μ*2=1.0,k*2=2.0,k1a=0.5(b) α0=90°,μ*1=1.0,μ*2=1.0,k*2=0.5,k1a=0.5圖6 出平面波入射時DSIF隨c/a的變化Fig.6ThedistributionofDSIFatcracktipvs.c/aimpactedbyincidentanti-planewave

(a) k*1=1.0,k*2=0.5,μ*1=1.0,μ*2=1.0,c/a=0.5(b) k*1=1.0,k*2=2.0,μ*1=1.0,μ*2=1.0,c/a=0.5圖7 出平面波入射時DSIF隨α0的變化Fig.7ThedistributionofDSIFatcracktipvs.α0impactedbyincidentanti-planewave

5　結　論

(1) 應用Green函數法研究了含有界面脫膠襯砌及其邊緣直裂紋的全空間在任意角度入射的出平面波作用下所產生的位移場和應力場。

(2) 通過數值計算結果討論可得出，襯砌及其周邊介質的物理參數參數、裂紋和襯砌的幾何參數參數以及入射波參數的變化對DSIF有影響。

(3) 通過對比分析可以得出，裂紋和襯砌的幾何參數的變化對DSIF變化幅度的影響較小。

[1] 楊在林.界面可移動圓形剛性夾雜對反平面波散射和它的遠場解[D].哈爾濱:哈爾濱工程大學,2000.

[2] 齊輝.界面圓環形襯砌對反平面波散射及動應力集中[D].哈爾濱:哈爾濱工程大學,2000.

[3] 趙春香,齊輝,楊在林,等. 半空間內孔邊界面裂紋對SH波的動力響應[J]. 振動與沖擊,2014,24:169-172.

ZHAO Chun-xiang,QI Hui,YANG Zai-lin,et al.Dynamic response of interface cracks originating at an hole in a Half-space to SH-wave[J].Journal of Vibration and Shock., 2014,24:169-172.

[4] Nan Jing-fu, Qi Hui, Shi Yong. Scattering of SH-waves by cylindrical lining debonded near bi-material interfaces[J]. Advanced Science Letters,2011,4(5):1281-1285.

[5] 南景富, 齊輝，折勇.垂直半空間界面裂紋及附近圓孔對SH波的散射[J]. 工程力學, 2009,26(5):245-250.

NAN Jing-fu,QI Hui, SHI Yong .Scattring of SH-wave by interface crack and neighbouring circular cavity in bi-material vertical half-space[J].Engineering Mechanics,2009,26(5):245-250.

[6] Qi Hui, Shi Yong, Nan Jing-fu. Ground motion of non-circular alluvial valley for incident plane SH-wave[J]. The 14th World Conference on Earthquake Engineering, 2008,10.

[7] 南景富,齊輝，韓劉，等.反平面波作用下地表覆蓋層與淺埋圓柱形夾雜的相互作用[J]. 自然災害學報，2010,2: 169-174.

NAN Jing-fu,QI Hui, HAN Liu,et al.Interaction between ground coverage layer and shallow buried cylindrical inclusion under action of SH-wave[J].Journal of natural disasters,2010,2: 169-174.

[8] Nan Jing-fu,Qi Hui,Zhao Chun-xiang. Scttering of SH-waves by interface semicircular debonded cylindrical lining and linear cracks originating at edge of lining[J].Advanced Materials Research,2012,399/400/401:2149-2154.

[9] 南景富, 齊輝. 含半圓形襯砌凸起彈性半空間問題的Green函數解[J].工程力學,2012,401(5): 31-36.

NAN Jing-fu,QI Hui.Green’s function solution of elastic half space including a semi-lining hill[J].Engineering Mechanics,2012,401(5): 31-36.

[10] 南景富. 界面圓形脫膠襯砌與裂紋對反平面波的散射[D]. 哈爾濱:哈爾濱工程大學,2012.

Scattering of anti-plane wave by a cylindrical lining with a disconnected curve and its edge’s linear cracks

NAN Jing-fu1, ZHAO Chun-xiang1, QI Hui2, YANG Zai-lin2, GAO Guo-fu1, YU Li-yan1, ZHAO Ji-tao1

(1. College of Science,HeilongjiangUniversity of Science and Technology, Harbin 150022, China; 2. Civil Engineering College, Harbin Engineering University, Harbin 150001, China)

The dynamic response of a whole space of homogeneous Bi-medium with an interface containing a circular lining with a semicircular degumming and its edge’s linear cracks to anti-plane force was studied with Green’s function. Firstly, the displacement fields described with Green’s functions were deduced for the upper half space with a semicircular hollow and the lower half space containing a cylindrical elastic lining with a semicircular hill when an out of-plane line source wave was applied on the horizontal interface. Secondly, the functions of incident wave, reflected wave, refracted wave and scattering wave were derived with anti-plane wave at any incident angle. Thirdly, linear cracks were constructed using the method of “cutting”, the upper and lower half spaces were joined to satisfy the boundary conditions in the conjunction area, and the governing equations of the solution were established. Finally, as an example,the numerical results for the dynamic stress intensify factor(DSIF) of the linear cracks were analyzed.

dynamic stress intensify factor(DSIF); semicircular disconnected curve; linear cracks; Green’s function; dynamic response of anti-plane force

10.13465/j.cnki.jvs.2016.13.024

黑龍江省自然科學基金項目(A201419)

2015-04-02修改稿收到日期：2015-06-19

南景富 男，博士，教授，1967年出生

O343.1

A