例題教學應從“解題”走向“思想”

張海強 孟盛

【摘 要】微積分是繼歐幾里得幾何之后，數學發展史中的一個創造，極限思想則是微積分的基礎。從歷史發展來看，極限思想的建立是一個漸進的過程，因此新課程教科書為幫助學生建立極限思想作了諸多嘗試。從高考對極限思想的考查來看，結果不盡如人意，因此宜加強習題教學的研究，使習題教學從數學知識的教學走向數學思想（方法）的教學，甚至數學觀念的教學。

【關鍵詞】極限思想；漸近線；下確界；數學閱讀；習題教學

【中圖分類號】G633.6 【文獻標志碼】A 【文章編號】1005-6009（2016）28-0039-03

【作者簡介】1.張海強，江蘇省宜興中學（江蘇無錫，214200）教師，高級教師，江蘇省特級教師；2.孟盛，江蘇省宜興中學（江蘇無錫，214200）教師。

極限思想是一種重要的思想方法，是微積分的基礎，是連接初等數學與高等數學的橋梁。隨著高中對導數內容學習的深入，極限思想不可避免地從幕后走向臺前，以“正統”的姿態進入了高中教材，極限思想已然成為高中數學思想方法的重要內容。但從2010年和2013年江蘇高考對極限思想的考查來看結果不盡如人意，學生尚缺乏運用極限思想解決問題的意識和能力，極限思想并沒有在學生的頭腦中“扎根”。本文以2010年和2013年江蘇省數學高考試題中的壓軸題為例，呈現考生的不嚴密解答，并做出相關分析，基于此給出對極限思想教學的一點思考。

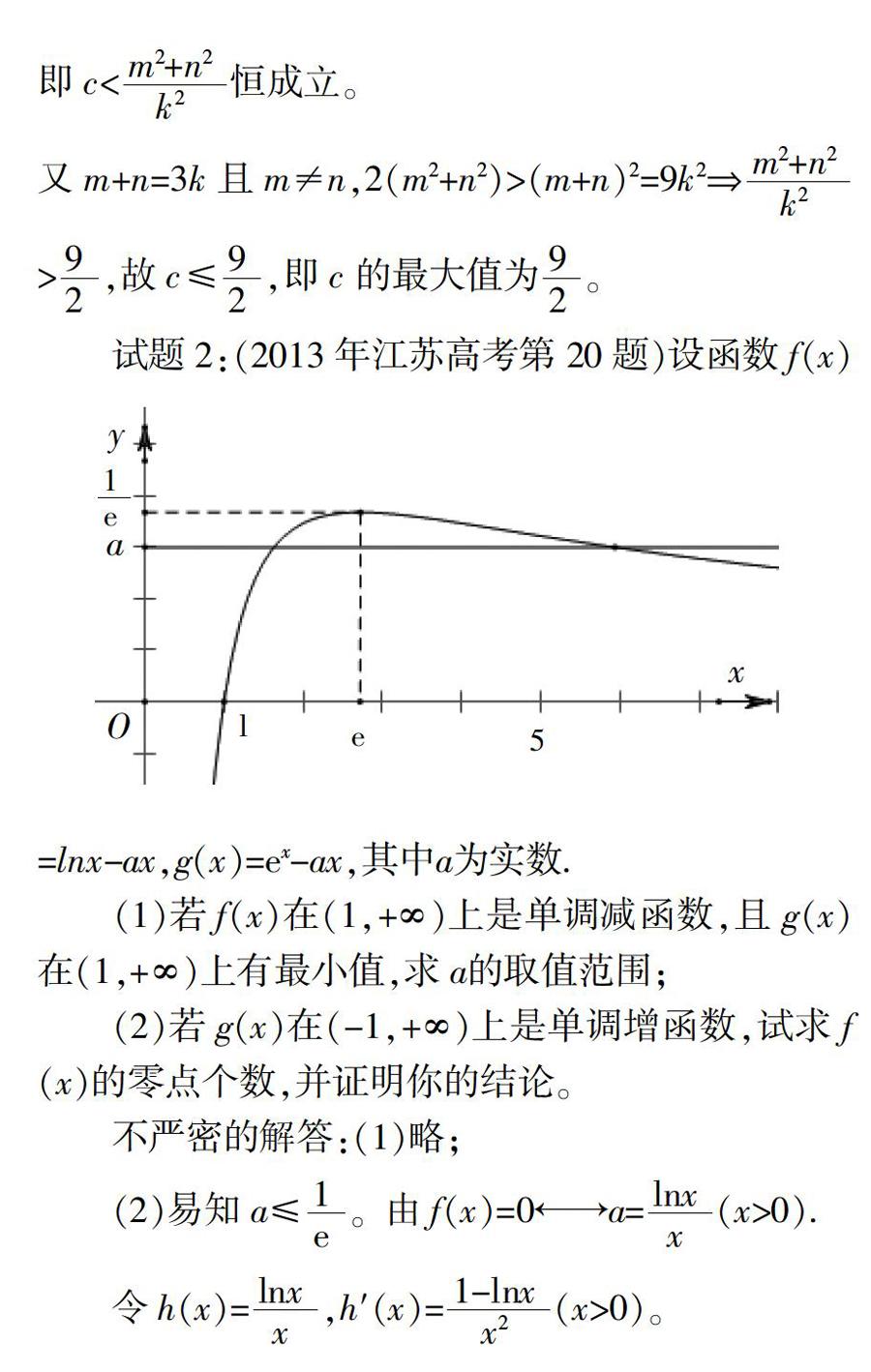
一、試題與不嚴密解答

四、兩點思考

首先，極限思想的建立是一個漸進的過程。就歷史發展的角度而言，極限思想的萌芽可以追溯到古代。在古希臘、中國和印度數學家的著作中，已不乏樸素的極限思想。如《莊子·天下篇》中的名言“一尺之棰，日取其半，萬世不竭”，劉徽的割圓術和古希臘的窮竭法等。17世紀英國物理學家牛頓與德國數學家萊布尼茲以無窮小概念為基礎創立了微積分，極限思想得到了進一步的發展。到18世紀極限思想得到初步的完善，法國數學家達朗貝爾等人先后對極限作出了各自的定義。19世紀法國數學家柯西比較完整地闡述了極限概念及其理論。由認知的歷史發生原理可知，學生頭腦中極限思想的建立應符合極限思想的歷史發展過程。

教科書在內容的編排上也充分考慮了這一漸進過程，以蘇教版高中教材為例，必修一“閱讀”欄目中“ 的含義”、必修二“問題與建模”欄目中“體積的近似計算”、“閱讀”欄目中的“祖暅原理”以及選修2-1正文中“雙曲線的漸近線的證明”等內容均為學生極限思想的建立提供了良好的素材和合理的時機。

因此，筆者以為應切實加強數學閱讀教學，而且首先從閱讀教科書開始，蘇教版高中教材中設置了“閱讀”“鏈接”“思考”“數學探究”等欄目，這些欄目的內容或有利于學生構建完整的知識的結構，或有利于擴展學生的數學視野、豐富學生的“智力背景”，或有利于參悟某種數學觀念。

其次，應當改進習題教學，立足于優化學生思維。蘇霍姆林斯基說：學生在課堂上的腦力勞動修養乃是教師勞動修養的一面鏡子。以此類推，學生在答卷上的腦力勞動修養何嘗不是教師勞動修養的一面鏡子？

試題1和試題2的不嚴密解答大多選擇“分離參數法”，這正是平時教學和練習中濫用“分離參數法”形成的思維定勢。因此，習題教學應著力提升學生分析問題的能力，注重通性通法，淡化技巧。

試題1和試題2的不嚴密解答說明學生對極限思想渾然不知，究其原因是教師在平時教學中缺乏高觀點的指導，缺乏極限思想的滲透，因此，習題教學應從數學知識的教學走向數學思想（方法）的教學，甚至數學觀念的教學。

試題1和試題2的不嚴密解答表現出了“千人一面”的現狀，究其原因是教師滿堂灌的結果，扼殺了學生的主動性和創造性，學生學會的僅僅是“依樣畫葫蘆”，臣服于教師的權威，缺乏質疑的品質。因此，習題教學需要留白，以提供學生“悟”的時間和空間，彰顯個人的特色與風采。

【參考文獻】

[1]華志遠.透視高考熱點，漫話極限思想[J].高中數學教與學，2014（17）.

[2]張海強，史豪峰.圖像固直觀，推理更精采[J].中學數學：高中版，2014（01）.