設計開放練習，打造活力初中數學課堂

秦燕

[摘 要] 數學練習是數學教學過程中最常見的一種鞏固、反饋、提升的訓練形式. 無論是課堂中的當堂訓練，還是課后的反饋訓練，我們要意識到練習的價值，需要教師用專業智慧和教育機智來挖掘其中的價值、優化其中的價值，最終更好地服務學生的發展.

[關鍵詞] 互動；多余；多解；隱藏；應用；初中數學

課堂練習對學生的意義重大，是促進學生溫故知新、鞏固新知的最有效方法之一. 但在以往的初中數學教學中，教師一直奉行題海戰術，認為只要做大量的練習，讓學生死記硬背概念公式，就是所謂的高效教學. 而事實上，恰好相反，這樣死板的練習模式，會讓學生逐漸形成固定的思維模式，不僅不利于學生的思考與發展，還會讓學生厭煩數學學習. 因此，在數學教學中，教師要善于為學生設計開放練習，給學生創造更大的思考空間，以更好地活躍學生的數學思維，培養學生各方面能力的發展.

設計互動型開放練習，活躍課

堂學習氛圍

在以往的數學練習課堂中，教師更多的是讓學生直接做題，大多數情況下，是教師出題學生做. 這樣的練習模式顯得很枯燥，學生的注意力較易分散，學習效率也不高，在很大程度上，這些練習是教師結合多年的教學經驗命制的，而這種經驗是單方面的，學生思維中需要達成的高度很難從練習題目中體現出來. 因此，教師必須創新、改變. 可以在數學練習課堂中，根據具體教材內容，為學生設計互動型開放練習，讓學生互相出題做題，以活躍學生的學習氛圍，提高學生的做題效率.

如教學“有理數的加減法”時，教師可選擇將課題交給學生，充分發揮其主體作用. “現在你們同桌互相出幾道關于有理數加減法的練習題，然后互相交換著做. 現在，你們每個人都是一名小老師，你們還要為其判對錯. ”學生在教師說完活動規則后，都很興奮、主動地投入到活動中. 這時，有學生為同桌出了這樣幾道題：-2+23=______；-28-3+12=______；55-（-12）+（-36）=______. 其同桌很快就給出了答案，并將自己所給的答案交給“小老師”. 學生由于“小老師”這一角色，都表現得很認真負責，不僅認真地判對錯，還從中尋找出錯的原因. 學生在檢查別人的錯誤時，也是對自己的一種檢驗，可以很好地汲取他人優點，反思自己的不足，并以他人的錯誤為警戒. 還有的學生能在自己的“學生”出現錯誤后，很好地為其講解，間接地做到了互幫互助.

教師為學生設計互動開放練習，能有效地激活學生的學習熱情，讓學生有機會互教互學，這無形中讓學生學到了更多的知識技能. 這種練習模式能讓學生找到學習的樂趣和自信，讓學生樂于做數學練習，樂于學習數學.

設計多余型開放練習，培養學

生的批判思維

練習是檢驗學生學習狀況的最有效方法之一. 教學中，如果題型過于單一，練習條件也很簡單、單調，學生很容易形成機械化解題，久而久之，就會使學生形成固定的思維模式，這不利于學生思維的發展，有時甚至會限制、約束學生的思維發展. 因此，教師要嘗試為學生設計一些開放型練習，可以設計一些條件多余型練習，讓學生自己去判斷、采集有用的信息，篩取多余的條件，以更好地培養學生的批判思維能力，從而架起未知量與已知量之間的橋梁.

比如，教學“一元一次方程”時，教師為學生設計了這樣的練習：小明和小強今年的年齡之和是30，小寧和小強的年齡之和為28. 當小明像小強這樣大時，小強的年齡恰好是小明的一半，問小強今年幾歲. 很多學生都已經形成了一定的思維定式，認為在練習中，給出的條件都是有用的，而且都必須要被用上. 因此，很多學生在做這道練習時，會受思維定式的影響，一直糾結于題中給出的數字“28”. 很多學生會想到用一元一次方程的知識，列出方程式，但是會發現，自己所列的方程式中沒有用完題中的條件，于是懷疑自己是否做錯了，是不是還有什么地方沒有想到，甚至有的學生一直不敢下筆. 由此，教師需要引導學生學會批判，培養學生的批判思想，讓學生能夠找到題中一些多余的、擾亂自己思維的條件. 學生在教師的引導下，會意識到其中的“28”這一條件是多余的.

條件多余型開放練習的設計，打破了學生的固定思維模式，給學生創造了觀察、思考、選擇的機會，讓學生學會了批判選擇，有效地培養了學生的批判思維，活躍了學生的數學思維，服務了學生學習效率的優化.

設計多解型開放練習，培養學

生的創新思維

以往教師設計的數學練習形式比較單一，大多情況下都只有一種解題結果. 這不僅會讓學生形成思維定式，還會限制學生的思維空間，嚴重影響學生思維的進一步發展. 由此，教師在數學教學中，要學會創新，要設計一些開放型練習，可以適時地為學生設計一些一題多解的練習題，以開拓學生的思維，更好地培養學生的創新思維. 而且，長期進行開放型題目的訓練，學生的思維也會隨著條件的變化而變化，能有效地引領學生進行思維，訓練思維的寬度，促使學生思維能力的提升，真正引領學生達成以不變應萬變的學習效果.

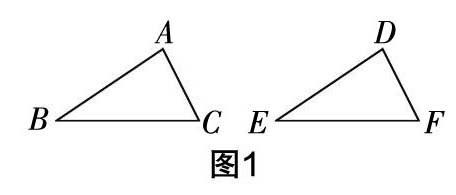
例如，教學“全等三角形”時，教師可為學生設計一道較為開放的練習，促使學生更進一步地思考. 首先，教師可給出一個圖形（如圖1），并告訴學生∠ABC=∠DEF，AB=DE，現在需要說明△ABC和△DEF全等，請他們添加一個條件. 這是一道開放的練習題，答案不唯一，能很好地開發學生的思維潛能，活躍學生的思維. 有的學生想到添加一個條件，使其最后滿足“SAS”的全等條件；有的學生想到添加一個條件，使其滿足“AAS”的全等條件；還有的學生則想到滿足“ASA”的全等條件. 學生在做完這道練習后，會對三角形全等的知識有一個全面的回憶和理解.

課堂教學中，通過設計多解型開放練習，能有效地挖掘學生的創新思維潛能，開發學生的智力. 一題多解型數學練習，給學生創造了更廣闊的思考空間，這種練習模式，能有效地培養學生的創新思維能力，推進學生全方面發展.

設計隱藏型開放練習，培養學

生的縝密思維

數學內容具有很強的邏輯性，是開發學生智力的最有效工具之一，初中數學在這方面表現的深度和廣度也顯而易見. 因此，在初中數學教學中，教師要善于開發、利用數學學科的這一資源. 我們可以從數學練習入手，注重培養學生的數學思維能力. 可以嘗試著設計一些條件隱藏型的開放練習，以培養學生的發現能力和觀察能力，進而更好地培養學生的縝密思維.

例如，教學“圖形的旋轉”時，教師在引導學生了解了有關旋轉的知識后，學生也都大體地了解到了旋轉的三個要素：方向、旋轉點、旋轉角度. 此時，教師可為學生設計這樣一道練習題：已知△ABC，且△ABC繞著其外一點O旋轉，現在已經知道點A和點B，經過旋轉后分別到達了點D和點E，需將旋轉后的三角形補充完整. 學生通過學習了解到，要想畫出旋轉圖形，首先要確定三個條件：旋轉方向、旋轉角、旋轉點. 通過觀察，他們發現這道題只明確給出了旋轉點，并沒有給出旋轉方向與旋轉角，一時間很多學生不知從何入手. 經過一番觀察、思考后，學生會發現那兩個條件其實都隱藏在其中. 即只要將對應點A，D與旋轉中心相連，就會構成一個角，這個角就是所謂的旋轉角，而所謂的旋轉方向根據D，E的位置也瞬間出現.教師在教學中通過設計隱藏型開放練習，能讓學生經歷較為深刻的觀察、發現、篩選、辨析等過程，讓學生在體驗中收獲、在體驗中成長，讓學生因經歷而體驗深刻，因深刻而記憶猶新，以此更好地培養學生的縝密思維，引領學生的智力生長.

設計應用型開放練習，培養學

生的應用能力

應用于生活，是學習數學的主要目的之一. 在數學教學中，教師要善于引導學生活學活用，而不是單純地記憶、機械地做題、強硬地死記硬背. 在設計練習時，教師要善于從學生的實際出發，設計一些應用型開放練習，以更好地鍛煉學生學以致用的能力，培養學生的應用能力.

在“二元一次方程組”的教學過程中，教師可為學生設計這樣一道應用型練習題：小明和小紅去書店買書，他們兩個喜歡上了同一本書，于是兩人各買了一本. 已知小明用了自己所有錢的五分之三，小紅用了自己所有錢的三分之二，而且小明最后剩下的錢比小紅多10元. 請問：兩人原來各有多少錢？他們買的這本書多少錢？

應用型練習的設計，能讓學生體驗到數學內容在生活中的應用價值，感受到數學學科的魅力，更能讓學生通過對實際問題的解決，感受到數學學習的重要性和必要性，進一步引領學生樹立正確的學習觀念，并通過解決這些問題，學會學以致用，學會變通，在長期的訓練和應用中，真真切切地提升學生的實際應用能力.

總之，在初中數學教學中，教師要善于打破固定練習模型，為學生設計一些開放型練習，給學生更多自由思考的空間，培養學生的思維能力，促進學生的全面發展.