深析例題 把握典型
孫靜
[摘 要] 如何真正提升學生的解題能力是我們當下需要深入研究的新課題. 解題能力,出發點在題目,因此,對典型例題進行深度分析,挖掘其價值,擴大其效益,變通其形式,是一種非常有效的方法和策略.
[關鍵詞] 遞進;薄弱;思維;解題能力
初中數學知識具有數量多、分散廣、變化活等特點,這些特征讓很多學生無法把握難點,在一些綜合性問題的應用過程中感覺無從下手,這也是讓很多學生感到知識接受困難的原因所在,也是教師們在開展教學活動時的關鍵著眼點. 對于數學知識與技能,似乎很難將其內容一一羅列出來,因為它的變化可能性太多了,綜合性也比較強. 既然如此,我們就需要轉換思維對其進行分析. 正所謂“萬變不離其宗”,數學知識的變化一定是按照其內在規律和基本起點進行的,如果我們能夠抓住這個核心內容,便可以提綱挈領地將整個知識體系予以掌握. 例題在數學教學過程當中就起到了這樣的重要作用.
逐層遞進,搭建問題梯度
例題經常會被運用在新知識的首次呈現過程中. 由于每個學生的知識基礎與接受能力存在差異,對于以新知識為內容的例題自然也會產生不同的感知. 這時,如果教師只在例題當中為學生提供唯一的接受選擇,難免會造成不同能力水平的學生無法找到真正適合自己的學習訓練平臺,進而造成知識學習效果的弱化. 因此,在課堂上設置有一定難度、梯度的例題便顯得尤為重要.
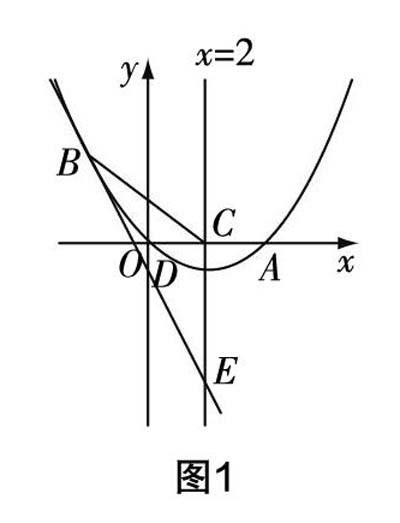
例如,在對拋物線內容進行深度講解時,筆者采用了這樣一道例題:
如圖1,拋物線過直角坐標系的原點O和x軸上一點A,其對稱軸是x=2,且與x軸交于點C. 直線y=-2x-1經過拋物線上的點B(-2,m),且與y軸及x=2分別交于點D和點E.
(1)求m的值及拋物線的函數解析式;
(2)求證:BC=CE,且點D是BE的中點;
(3)若點P(x,y)是拋物線上的動點,是否存在合適的點P使得BP=EP?
這道例題呈現出了十分明顯的難度梯度,解答問題的同時,學生們的思維能力自然而然地隨之深化了.
問題梯度的存在對于數學教學來講具有三個方面的意義:第一,將一個難度較大的問題劃分為幾個層次分別呈現出來,無形之中縮小了每一個問題之間的難度差距,學生接受起來也就更加輕松,不但能激發學生的參與興趣,還能滿足班級不同層面學生的需求,能真正達成隱性分層的效果. 第二,分梯度的問題為學生們的知識接受提供了更多選擇,大家可以根據自己的現有能力去選擇相應問題進行解答,既能實現能力的有效提升,又不致由于問題難度過大而打擊信心. 第三,問題的分層遞進無形之中也暗示了這類問題的解決方法,讓學生學會將一個較為復雜的問題分解成幾個簡單的問題,從問題的根源慢慢挖掘、分析,以此達成方法建構的效果.
找尋捷徑,提高解題效率
隨著初中數學知識的逐步加深,復雜的問題出現得越來越多. 筆者將學生認為困難或錯誤率較高的問題進行總結后發現,學生之所以會出現解題錯誤,很大一部分原因在于沒有找到解題捷徑. 特別是對于一些計算類型的問題來說,“繞路走”往往會增加很大的錯誤風險.
例如,學習因式分解的內容時,筆者以(x2-3x+2)(x2-3x-4)-72為例向大家進行了講解. 面對這道題,我沒有讓學生立刻動手計算,而是先耐心觀察,尋找其中的特點. 果然,大家發現,在兩個括號當中,(x2-3x+2)可以視為一個共有的整體,以此為基礎進行十字相乘. 于是,學生試著將(x2-3x+2)設為t,原式則轉化為t(t-6)-72,進而展開后得t2-6t-72. 這便成為學生所熟悉的因式分解類型,問題自然迎刃而解. 相比于直接將題目當中的兩個括號相乘展開成四次多項式再進行分解,這個方法顯然快捷得多.
解答數學問題的捷徑多種多樣,教師不可能將所有的技巧向學生講述完全. 教師要給予學生的,是發現捷徑的眼睛,讓學生學會用自己的思維去分析、篩選方法,并選擇一種最適合的方法去解決相應的問題. 如果學生都能從每一道典型例題當中總結出一個解題方法,日積月累下來,將是極大的財富,同時,學生的解題能力也會逐漸得到提升.
找準失誤,修補薄弱環節
一道例題提出之后,把它的答案解出來就結束了嗎?當然不是. 例題不僅僅是對所學知識進行實踐練習的工具,更是建立完善相應知識體系的絕佳契機. 如果教師能夠帶領學生以這個更高的視角對例題的作用進行認知,那么對于高效運用例題、有效強化數學問題解答,很有好處.
例如,在對圓的內容進行教學時,筆者以這樣一道例題予以強調:在平面直角坐標系中,圓心O的坐標為(-3,4),以半徑r在平面內作圓,那么,當圓O與坐標軸有1個、2個、3個、4個交點時,r所對應的取值情況分別是怎樣的?這個問題看似簡單,卻不容易答對,特別是在后兩個問題的解答中,很多學生沒有將情況考慮完全. 問題解答完畢后,筆者特別對此進行了分析,并引導大家找到出現錯誤的原因. 在圓的問題分析中,對基本概念的理解以及數形結合方法的運用,得到了大家的關注.
對例題的解答一定不會總是一帆風順. 無論學生最終能否將例題正確地解答出來,其中所出現的困惑疑難之處都應當被教師捕捉并加以關注,這將是促進學生解題能力提升的關鍵所在. 讓學生經歷失敗、分析失敗、戰勝失敗,才能真正讓失敗成為成功之母. 在學習時,教師一定要引導學生不要過多地關注自己會什么,而應勇敢地面對自己不會什么. 通過對例題解答過程當中出現的薄弱環節進行分析與強化,能讓學生的學習弱點得到及時彌補,并從中總結出更為凝練的問題解答方法,教學效果遠比單純地引導學生解答問題要理想得多.
學以致用,以生活釋理論
在數學知識的教授過程中,時常會談到生活的元素. 在實際生活當中,也總是可以找到數學知識的影子. 這不僅表明了數學理論與實際生活當中的密切聯系,更明確了在數學的理論學習當中滲透實際生活的重要性. 這也為教師的例題選擇提供了指引,即只有在例題當中融入實際生活的內容,才是完整、有效的. 也只有這樣,才能讓學生感受到數學學習的價值所在,更能激發學生對數學的內在學習動力.
例如,在對一元二次方程的內容進行教學時,筆者向同學們提出了這樣一個問題:小張所在的公司在每年一月份都會給員工漲月工資. 小張2008年的月工資是2000元,到了2010年,漲到了2420元,且2011年的月工資繼續按照2008年到2010年的月工資平均增長率增長. 那么,小張2011年的月工資是多少?這道例題的難度并不算太大,但其解答思路卻非常明確地指向了一元二次方程. 通過將月工資的平均增長率設為x,列出方程2000(1+x)2=2420之后,問題順利求解,這也是數學理論知識在實際生活當中的直接體現.
加入生活元素之后,原本抽象枯燥的數學理論一下子具體、靈動起來了. 實際生活以其特有的方式闡釋了理論的內涵,并向學生指明了拓展知識視野的方向. 在實際生活的輔助之下,學生以全新的視角認知了理論知識,并在解決實際問題的同時延伸了思維,實現了理論方法的靈活適用.
提煉總結,提升思維水平
例題之所以能夠成為當前所學知識內容的示范,就是因為其中具有比較明確的代表性. 這種代表性不僅表現在知識內容本身,還有其背后的思維方法. 初中階段的學生還沒有形成成熟、完善的數學思想,很少能夠站在宏觀角度總結解題規律,這也是解題效率不高的原因之一. 教師們正好可以從例題入手,提煉總結,為學生的解題打開捷徑.
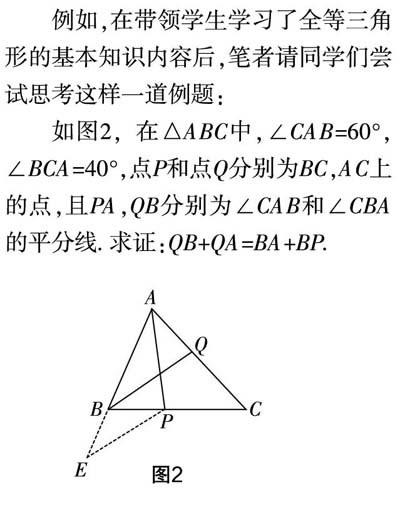
例如,在帶領學生學習了全等三角形的基本知識內容后,筆者請同學們嘗試思考這樣一道例題:
如圖2,在△ABC中,∠CAB=60°,∠BCA=40°,點P和點Q分別為BC,AC上的點,且PA,QB分別為∠CAB和∠CBA的平分線. 求證:QB+QA=BA+BP.
這個問題的證明過程采取了延長AB至點E使BE=BP,連接PE的輔助線構造方法,通過證明△APC和△APE全等得出AC=AE,進而將相等線段進行轉換,結論得證. 從這個問題當中可以總結出,當需要證明線段之間的和、差以及倍數關系時,將長線段進行分解或將短線段加長,是一個管用的規律性方法.
可以說,只有抓住每一道例題,將其中的思想方法總結出來,才算是將這道題真正解答明白了. 這個過程也將學生的思維水平提升到了一個新高度. 將這種思想用于具體問題的解答當中,無疑是一種效果的升華.
以具體問題闡述知識內容,是初中階段數學課堂教學當中,經常會運用到的方式. 然而,驗證理論知識并不是例題存在的全部意義,它在呈現代表性知識內容、為靈活的數學變化提供根本依據當中也起到了決定性作用,這不僅完善了我們對于數學例題價值的認知,更為教師們的例題選擇與設計提供了更多啟示. 我們一定要盡可能地讓例題的示范性作用達到最大化,讓同學們在掌握了一道例題之后,便可以對相關的整個知識鏈有所感知,并以例題為抓手,實現知識內容學習的深入與知識能力的提升.

