開發利用初中數學課程資源的探索

潘優紅

摘 要 教師應該深入挖掘教材上的例題、習題的教學功能，做到既立足教材，整合和優化教材，又能夠超越教材，開發課程資源，有效服務數學教學。本文通過研究中考題目，聯系教材例題，探討了創編數學習題有效開發利用初中數學課程資源的問題。

關鍵詞 課程資源 習題創編 習題教學 初中數學

中圖分類號：G633.6 文獻標識碼：A 文章編號：1002-7661（2016）09-0067-03

數學習題教學不僅僅只是在形式上的示范，更應該是對于知識重點和難點突破的良好載體。這就需要教師靜下心來，深入鉆研課標和教材，弄懂教材的重點、難點和知識間的聯系，在教材的運用上采取調適取向，在教學的方式上采取創生取向，不斷創編符合教材和學生實際的習題。教師在創編中培養自己調整教材、創造性的使用教材的能力，一定能夠挖掘教材的潛在因素，創編出像中考題那樣精彩的補充習題，從而開發和利用好初中數學課程資源，有效拓展學生學習的空間，為提高學生綜合數學素養服務。

一、有效創編習題的原則和要求

1.基本原則：立足教材，超越教材

教師教育學生的目的是培養他們發現問題、解決問題的能力，學習新事物的能力，提出更一般、更廣闊的、更深層次的新問題和建立新理論的能力。因此，有效補充習題并不是簡單、盲目地更換教材內容，更改例題的情境與數據，甚至是大刀闊斧地拋卻教材，對教學內容進行重新設計。它應該是教師在仔細研讀和分析教材后，在充分了解和把握課程標準、學科特點、教學目標、教材編寫意圖的基礎上，立足于學生的學習需要，以教材例題和習題為藍本，根據學生的實際情況并結合具體的教學環境，利用現有的教學資源，充分發揮教師的個人教學特長和創新能力，靈活有效地組織教學，有計劃、有目的地對教材進行活化、改編及重構，實現對教材的必要超越，從而拓展教學空間，促進學生的主動發展。

2.具體要求：變通使用，拓展空間

教師要深刻認識到包含在這些素材性資源之中的隱性資源，在基礎知識的教學中強調從原型出發上升到抽象的數學知識，暴露思維，讓學生體驗知識產生的過程。從課本例題、課本習題出發，讓學生把所學知識在更大范圍內進行歸納、演變，使知識形成一個更加完整的網絡。從變通出發，通過變換題目的表面形式讓學生準確把握知識的深層結構，通過變式訓練強化學生的理解和掌握，實現開發數學思想方法等隱性資源的目的。教師還可以針對課本內容設計一些開放性的教學內容，為學生的創造性學習提供必要的素材。

（1）針對性。應圍繞數學知識的本質屬性選擇習題，淡化這些事例中的非本質屬性，以免干擾數學知識的形成，真正達到鞏固知識、活化思維的目的。

（2）可比性。既要設計所要形成數學知識的正例，又要設計不符合這一知識的反例，正例與反例應當容易識別，能讓學生明顯區分它們的某些不同屬性。

（3）適量性。習題要有一定的數量，數量太少，不足以形成知識與技能；數量太多，會浪費學習時間并且使學生感到乏味。

（4）趣味性。習題應盡可能生動、有趣，語言要簡練，有利于激發學生的興趣，還可借助于實物、模型、圖片、錄像、課件等多種形式引入習題。

（5）參與性。一般來說，創編習題的目的是為了選取學生更感興趣的教學內容與活動，深入學生的精神世界，從而激發學生的學習興趣，使他們產生強烈的學習動機，最大限度地激發學生探究的欲望。有了動機，學生才能自主探索、大膽質疑，積極、主動地去學習。因此，教師要及時組織學生對創編的習題進行思考、討論、動腦、動手，參與課堂教學活動，調動他們的學習積極性和主動性。

二、例析創編習題的有效策略

1.原題呈現

浙教版教材九年級（上）有這樣一道題：有一塊三角形余料ABC，它的邊BC=120mm，高AD=80mm。要把它加工成正方形零件，使正方形的一邊在BC上，其余兩個頂點分別在AB，AC上。問加工成的正方形零件的邊長為多少㎜？

【解題點撥】本題的解答非常簡單，只要利用PN∥BC，得到△APN∽△ABC，再利用相似三角形的性質即可得解。本試題難度不大，主要考查學生綜合運用相似的知識解決實際問題的能力。

【問題賞析】題目以學生熟悉的“平面圖形（三角形和四邊形）”為載體，將數學蘊涵于平面圖形的探究變化之中，搭建起一個讓學生真正思維起來的研究平臺，極富啟發性、開放性、再生性和思維性，具有極大的自由度和探索空間。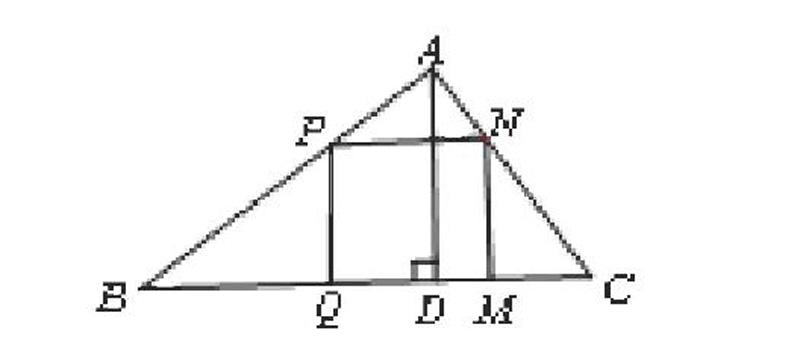

2.立足教材，在重組中激發興趣，促進學習

教材作為學生從事數學學習的基本素材，教師應充分認識到這僅是提供給師生的一個情境、一個問題、一條思路，在這個情境、問題和思路面前，教師完全可以展示自己的教育智慧，以有利于學生開展學習活動為追求目標，在尊重學生的認知發展和知識的邏輯順序前提下勇于對教材進行合理、適度、準確的開發。對于教材中靜態方式呈現的主題情境，可以根據需要改變為動態的實際場景；也可以將脫離本地學生實際的情境內容適當調整或更換，或根據學生的現實學習水平，對主題情境呈現的內容進行適當重組。教師可根據教學目標的要求，遵循學生的學習規律和學習實際，通過恰當的重組教材，引導學生經歷數學化的過程，引導每個學生主動參與到數學活動中來，以提高課堂教學的有效性。教師可以補充湖北鄂州中考24題：如圖所示，某校計劃將一塊形狀為銳角三角形ABC的空地進行生態環境改造。已知△ABC的邊BC長120米，高AD長80米，學校計劃將它分割成△AHG、△BHE、△GFC和矩形EFGH四部分（如圖）。其中矩形EFGH的一邊EF在邊BC上，其余兩個頂點H、G分別在邊AB、AC上。現計劃在△AHG上種草，每平方米投資6元；在△BHE、△FCG上都種花，每平方米投資10元；在矩形EFGH上興建愛心魚池，每平方米投資4元。

（1）當FG長為多少米時，種草的面積與種花的面積相等？

（2）當矩形EFGH的邊FG為多少米時，△ABC空地改造總投資最小？最小值為多少？

問題⑴是將原課本題適度引申，原題中的正方形變成矩形，所考查的知識與課本題類似，本題利用相似三角形的性質將矩形的另一邊長用FG來表示，再列方程求解。對于問題⑵△ABC空地改造投資最少，言下之意是四邊形HEFG面積最大，又回到原課本題的解題中。

從教學的實際效果來看，這個增補的習題使學生興趣倍增，大家躍躍欲試，紛紛利用所學的知識進行解答，課堂氣氛達到了高潮。看來，除了教材中有限的習題外，教師還可以做個有心人，細心觀察、用心尋找生活中與數學學習相關的素材，進行創造性地加工，設計成新穎的練習，用以輔助教學。

3.以生為本，在改編中促進學習，挖掘潛能

教師用教材就是根據學生的認知水平、心理特征、學習規律而定，因此教師要認真研究學生的現實水平，所要補充的習題既要立足現實水平，又要挑戰學生潛在水平。教師可以補充山東東營中考24題：如圖，在銳角三角形ABC中，BC=12，△ABC的面積為48，D、E分別是邊AB、AC上的兩個動點（D不與A，B重合），且保持DE∥BC，以DE為邊，在點A的異側作正方形DEFG。

（1）當正方形DEFG的邊GF在BC上時，求正方形DEFG的邊長；

（2）設DE = x，△ABC與正方形DEFG重疊部分的面積為y，試求y關于x的函數關系式，寫出x的取值范圍，并求出y的最大值。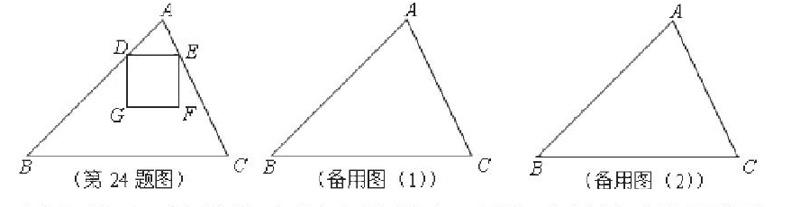

以生為本，從學生實際出發補充習題，應該注意以下兩點：

（1）根據學生新舊知識的聯系創編習題。課堂教學過程是將教材的知識結構轉化為學生的知識結構過程。這一過程實現取決于教師能否從學生的知識水平出發，幫助學生找準新舊知識的聯結點，使新舊知識之間建立起聯系，使學生學會用舊知去同化新知，從而學會學習。本題的條件中沒有告訴三角形的高，但可以啟發學生思考，根據底和面積順利求出。問題⑴的求解其實就是課本題重現，解答方法與課本題目一樣。

（2）從學生的生活經驗出發創編習題。建構主義認為：復雜的學習領域應針對學習者先前的經驗和學習者的興趣。只有這樣才能激發學習者的學習積極性，學習才可能是主動有效的。問題⑵的求解高于課本題，求解要注意分類，因為重疊部分可能在三角形內部，也可以在三角形的外部。這樣讓學生能通過動口、動手、動腦，親自參與再創造，更輕松、更深刻地感知和理解所學的知識，更好地掌握解決問題的策略與方法，形成良好的數學思維品質，從而學會用數學的眼光去分析問題、解決問題。

4.教給方法，在創編中落實主體，學會學習

學生是數學學習的主人，通過數學學習，學生不僅要掌握知識，而且更重要的是學會運用所學的知識，在不斷地學與用中提高能力。所以，在教學中，教師要善于教給學生數學學習的思想方法。數學思想方法是數學知識在更高層次上的抽象和概括，它蘊含于知識發生、發展和應用的過程之中，是知識轉化為能力的橋梁，數學能力的高低往往表現在對數學思想方法的理解和運用上。因為學生所做的題目，以及教師所選的例題不過是一種知識載體。教師的任務就是通過這一知識載體去發現、挖掘其中不變的數學內涵，即數學的基礎知識和基本技能、數學的通性通法。抓住了通性通法，就抓住了數學對象的基本性質。因此，教師要立足課本例題，創造性地選用和創編題目，幫助學生體會函數與方程的思想、等價轉化的思想、分類討論的思想、數形結合的思想等重要思想方法在數學解題中的應用，要把總結與反思解題的思維過程成為數學思想方法的滲透、領悟、升華和應用的過程，使學生自覺地運用數學思想方法指導數學解題。學生掌握了思想方法，才能主動地、積極地去探究新知，鞏固舊知，形成自學能力。比如在初中數學教學中，有時將問題看成一個整體時，則無從下手，若分而解之，各個擊破，則能柳暗花明。分類討論正是這一種思想，為了解決問題，將問題所涉及的對象不遺漏地分成若干類問題，然后逐一解決，從而最終解決整個問題。通過向學生講解分類討論這個方法，就會提高自身靈活遷移理解數學知識的能力。教師還可以補充福州中考21題：如圖，在△ABC中，∠C=45埃珺C=10，高AD=8，矩形EFPQ的一邊QP在邊上，E、F兩點分別在AB、AC上，AD交EF于點H。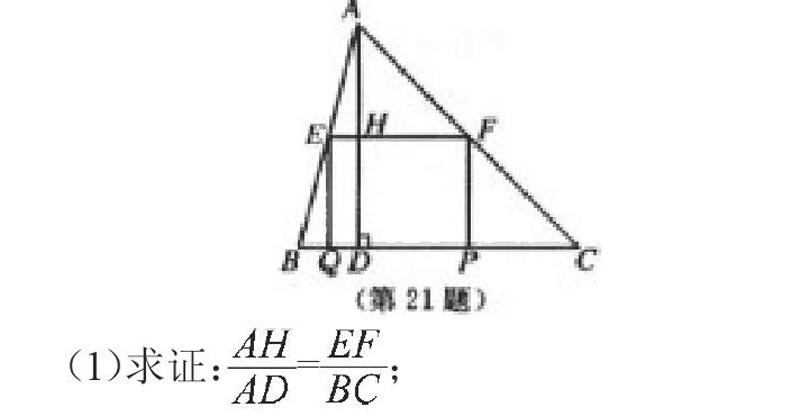

（2）設EF=x，當x為何值時，矩形EFPQ的面積最大？并求其最大值；

（3）當矩形EFPQ的面積最大時，該矩形EFPQ以每秒1個單位的速度沿射線QC勻速運動（當點Q與點C重合時停止運動），設運動時間為t秒，矩形EFPQ與△ABC重疊部分的面積為S，求S與t的函數關系式。

問題（1）是考查相似三角形的性質，容易得證。問題（2）表面上看是一個求二次函數最值的問題，其實是課本原題的拓展與延伸，它也是利用比例線段的性質，將矩形的另一邊的長用含X的代數式表示；然后建立面積關于變量X的函數關系式再求最值。問題（3）又與動態的問題相結合，考察學生運用相似解決動態問題，這類問題有利于培養學生的思維能力。這類問題通常運用分類討論的數學思想，解答這類問題有一定難度，需要學生具備獨立的鉆研精神，教師要經常進行訓練。

當然，用分類討論思想解題，在數學解題中占據重要地位，用分類思想解題不僅可以加深對數學基礎知識和基本技能的理解，而且也有助于理性思維能力的提高。但是，有時在分類討論時，會造成解題過程的繁瑣，這就要求我們在解分類討論題目時，注意解法上的優化，對有一些題目，可以采用其它解法，使分類討論得以避免和簡化。

可見，數學題目情境千變萬化，形形色色，教學中想要以有限的題型來給它們編號掛點，這無疑是大海撈針。因此，課堂中必須幫助學生從總體上條理出解決問題的本質思路，引導學生抓住貫穿于各種類型問題的“紅線”，即數學思想方法。我們在平時教學中不應過分地追求特殊方法和特殊技巧，不必將力氣花在鉆難題、怪題和過于繁瑣、運算量太大的題目上，而應將主要精力放在基本方法的靈活應用和提高學生的思想層次上。因此，為了將能力的培養落到實處，重視數學思想方法的提煉和滲透顯得尤為重要。

三、結語

教師不單純是課程的接受者，同時也是課程的調適者和創生者。有效創編數學習題，既可拓展學生的解題思路，又可培養學生的探究發現能力。只要教師發揮自己的創造能力，根據學生的學情對習題進行整合和創編，前“鋪”后“繼”，才能讓學生學得輕松，學得愉快！

參考文獻：

[1]袁永昌.初中數學教師開發課程資源的現狀分析[J].新課程，2008，（4）.

[2]何國光. 例談初中數學課程資源的有效開發與利用[J].數學學習與研究，2010，（10）.

[3]康利燕.談數學課程資源的有效開發和利用[J].西部素質教育，2016，（3）.