2016 年高考數學全國卷試題評析與新一輪高考數學復習建議(上)

◇ 北京 丁益祥(特級教師)

(作者單位：北京陳經綸中學)

?

2016 年高考數學全國卷試題評析與新一輪高考數學復習建議(上)

◇ 北京 丁益祥(特級教師)

1 試題總體評價

2016年全國高考數學甲、乙、丙3套試題,都依照考試大綱的要求,較好地堅持了“考查基礎知識的同時,注重考查能力”的原則.在以能力立意的命題思想指導下,著意將知識、能力與素質融為一體,全面檢測了考生的數學素養.

試題注意了數學的學科特點,突出了知識的基礎性和綜合性,以主干知識為主體,注意在知識網絡交會點設計試題.著力體現概念性、思辨性和應用性,在數學思想、理性思維以及數學潛能方面都作了比較深入的考查.試題總體難度適中,除了個別把關試題較難外,大部分試題平和穩定、似曾相識、穩中有變、推陳出新.既考查了中學數學的知識和方法,又檢測了考生進入高校繼續學習的潛能,發揮了數學作為基礎學科應有的作用.

2 主要特點分析

2.1 在考查雙基中凸顯重點內容

2016年的數學《考試大綱》在考查要求中明確指出:“對數學基礎知識的考查,既要全面又要突出重點,對于支撐學科知識體系的重點內容,要占有較大的比例,構成數學試題的主體.”

《考試大綱》的這一命題要求,在2016年全國甲、乙、丙3套數學試題中都得到了較好的落實.試題一方面對高中數學所涉及的概念、性質、公式、法則、定理、公理等都作了較為全面的考查,知識點覆蓋面約占所有知識點的65%;另一方面凸顯了對導數與函數、三角函數(包括三角恒等變換和解三角形)、平面向量與空間向量、數列、不等式、概率與統計、圓錐曲線與方程、空間圖形與平面圖形等8個重要部分內容的考查.

我們以2016年全國甲、乙、丙3套理科試題作說明見表1.這些都充分說明在全面考查雙基的同時,凸顯重點內容重點考查、重點內容反復考查的命題特點.

表1

2.2 在考查交會中提高學科能力

2016年甲、乙、丙3套數學試題,都十分重視從學科的整體高度和思維價值的高度,凸顯對知識網絡交會問題的考查,據此檢測學生的數學能力.

(1) 證明|EA|+|EB|為定值,并寫出點E的軌跡方程;

(2) 設點E的軌跡為曲線C1,直線l交C1于M、N2點,過B且與l垂直的直線與圓A交于P、Q2點,求四邊形MPNQ面積的取值范圍.

分析與評述 此題第(1)問是2條線段長度之和的定值問題和動點的軌跡問題,充分利用平面幾何中圓的性質、等腰三角形的性質以及平行線的性質,不難證明|EA|+|EB|等于已知定圓的半徑,當然是定值.再結合橢圓的定義,即可判斷動點E的軌跡是橢圓,進而可寫出其方程.

解決第(2)問的前提是求出四邊形MPNQ的面積函數,然后確定其取值范圍.注意到這個四邊形的4個頂點是由直線l與第(1)問中求出的橢圓C1的交點,以及過點B且垂直于l的直線與已知圓的交點所確定的,這自然想到應考慮直線l斜率的存在與否,所以應分“直線l與x軸不垂直”和“直線l與x軸垂直”2種情況討論.此外,無論是上述哪一種情況,都可以把四邊形分割成2個三角形來處理.為此需要通過弦長公式或圓的半徑、弦心距以及半弦所構成的直角三角形,利用勾股定理求弦長,然后根據上述2種情況再確定四邊形面積的取值范圍.

顯然,此題突出了解析幾何與平面幾何的交會,具有較強的綜合性,著重考查了直線與圓及橢圓的位置關系、橢圓的定義、弦長公式、平行線的性質、勾股定理、三角形面積等知識,考查了分類與整合的思想以及運算求解能力和推理論證能力.通過此類問題求解,可以有效地檢測和提高學生的數學能力.

2.3 在考查應用中強化應用意識

數學應用問題的考查由來已久,2016年應用問題在保持考查概率與統計模型的基礎上,又關注了其他數學模型應用問題的考查.

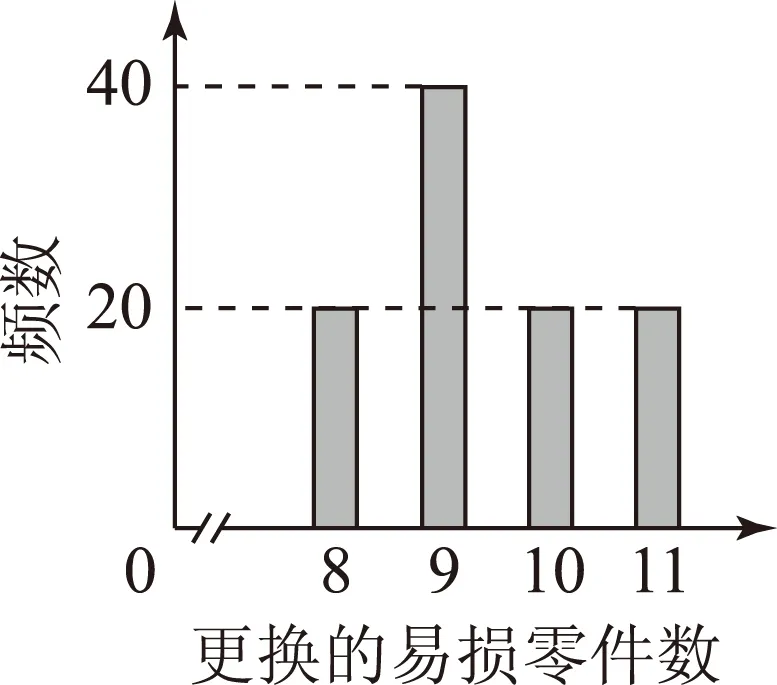
圖1

(1) 求X的分布列;

(2) 若要求P(X≤n)≥0.5,確定n的最小值;

(3) 以購買易損零件所需費用的期望值為決策依據,在n=19與n=20之中選其一,應選用哪個?

分析與評述 第(1)問給出了關于100臺這種機器在3年使用期內更換的易損零件數的柱狀圖,并且在“以這100臺機器更換的易損零件數的頻率代替1臺機器更換的易損零件數發生的概率”的條件下,求2臺機器3年內共需更換的易損零件數X的分布列.核心是X可取值的確定及相應概率的分析和計算.

第(2)問是在第(1)問基礎上的自然引申.事實上,只需根據第(1)問所求出的X的分布列,通過計算、比較,便可以確定n的最小值.

處理第(3)問,首先應弄清購買零件的費用所包括的2個方面:1)購買機器時同時購買的零件所需費用,按每個200元計算; 2)備用零件不足時另外購買的零件,按每個500元計算.在此基礎上,分別計算n=19與n=20這2種情況下各自所需費用的分布列,進而求出期望,再比較大小,即可作出正確決策.

不難看出,此題著重考查離散型隨機變量的分布列和期望.后2問從經濟核算的角度,考查了在數理統計基礎上的理性決策,體現了概率統計知識在實際問題中的應用.這種概率統計知識的命題方式,既是近幾年高考試題的熱點,又是亮點,具有濃郁的應用味兒,它有效地檢測了學生的應用意識和實踐能力.

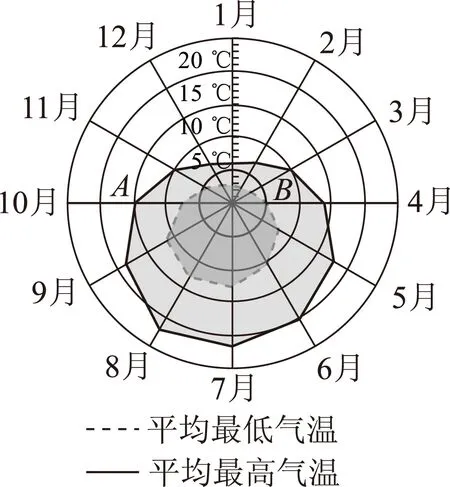
圖2

A 各月的平均最低氣溫都在0℃以上;

B 7月的平均溫差比1月的平均溫差大;

C 3月和11月的平均最高氣溫基本相同;

D 平均氣溫高于20℃的月份有5個

分析與評述 由雷達圖可看出:對于選項A,0℃在虛線為邊界的圖形內,故各月的平均最低氣溫都在0℃以上,因此A正確.對于選項B,7月的平均溫差大于7.5℃,1月的平均溫差小于7.5℃,所以7月的平均溫差比1月的平均溫差大,因此B正確.對于選項C,3月和11月的平均最高氣溫大約都在10℃左右,所以3月和11月的平均最高氣溫基本相同,因此C正確.由此可知D錯誤,因此選D.

事實上,由雷達圖可看出,平均氣溫高于20℃的只有3個月份(6、7、8月),因此D錯誤.

此題是關于某城市氣溫情況的實際問題.問題的解決利用了雷達圖的閱讀和分析技術,這種技術是基于一種形似導航雷達顯示屏上的圖形而構建的一種多變量對比分析技術,雷達圖是統計圖中的一種,它由若干個同心圓以及從圓心向外引出的若干條射線構成.這些同心圓的間距相等,每個圓代表一定的指標值.解題時,通常將同一類變量不同時期的指標值依次連接成封閉折線,從而獲得不同類別變量不同的折線圖,再進行對比分析,進而作出相應的判斷.

這里,雷達圖只是這個旅游城市用來向游客介紹本地氣溫情況的一種形式.命制此題的弦外之音是數學應用意識的考查,除了概率與統計問題以外,還有涉及其他知識的問題.此題的考查為我們把握應用問題的復習內容和方向,提供了新的視角.同時,通過不同知識內容實際問題的考查,體現數學應用的廣泛性,以此不斷強化學生的數學應用意識.

(未完待續)

(作者單位：北京陳經綸中學)