交互式多系統跟蹤定位算法

張曉光　　魏東巖　　徐　穎　　袁　洪(中國科學院光電研究院　北京　100094)

?

交互式多系統跟蹤定位算法

張曉光*魏東巖徐穎袁洪
(中國科學院光電研究院北京100094)

摘要：交互式思想在多模型定位中獲得廣泛應用，但在多系統跟蹤定位中應用較少。該文借鑒交互式思想提出交互式多系統跟蹤定位算法。該算法利用已獲得的估計信息進行系統間定位信息的直接交互，然后進行多系統并行濾波，并利用各系統濾波新息和方差對系統概率進行實時更新，將估計結果按照系統概率加權融合輸出。通過跟蹤機動目標的仿真實例，可以看出該算法能夠根據定位系統的性能及時調整系統概率，有效改善多系統下目標跟蹤定位性能。

關鍵詞：多系統跟蹤；交互式；系統概率

1　引言

文獻[1]提出的交互式多模型(Interacting Multiple Model，IMM)算法在機動目標跟蹤定位中得到廣泛應用[2]。其基本思想是通過多模型并行描述目標可能的運動狀態，依據貝葉斯理論通過新息動態調整模型概率，并將各模型濾波結果融合輸出。該算法有效解決了單一模型在目標運動狀態變化時的失真問題。針對IMM的相關研究層出不窮，文獻[3]和文獻[4]針對單一模型集對目標運動狀態覆蓋有限的問題分別提出了多模型集切換和基于K-L(Kullback-Liber)理論的模型集自適應的IMM算法，并有效避免了計算復雜度的提升；文獻[5]和文獻[6]分別提出自適應模型轉移概率調整IMM算法，有效解決了轉移概率固定不變對目標跟蹤定位性能的限制；文獻[7]提出了粒子濾波器與擴展卡爾曼濾波器(Extended Kalman Filter，EKF)并行的不對稱交互式濾波算法，有效解決了非線性和線性定位系統并存的問題。文獻[8]提出了隨機無跡卡爾曼IMM算法，有效解決了定位系統數據丟失與未丟失情況并存的問題。文獻[9]針對IMM實際應用中可能存在并行濾波器相關的情形，提出了一種基于濾波器估計誤差互協方差陣計算似然函數的標量權重交互式多模型算法(Cross-covariance Scalar weighted Interacting Multiple Model，CSIMM)，該算法計算量適中且能夠適用于惡劣的定位環境。

但是除了運動模型的限制，定位系統性能對目標跟蹤定位的影響也至關重要。傳統衛星導航單系統定位已經很難滿足需求，依靠各種傳感器建立的多系統融合導航定位技術被廣泛研究[10-12]。但將交互式理論引入到多系統定位中，解決系統間協作的研究還不多。文獻[13，14]提出多傳感器的交互式協作算法，但該算法還是對上一采樣時刻濾波的狀態向量進行交互，并沒直接對當前各系統定位信息進行交互，也沒考慮交互所對應的系統間誤差處理，協作定位中系統概率動態調整滯后，影響了跟蹤定位性能。

本文借鑒交互式的思想，提出一種多系統交互式(Interacting Multiple System，IMS)跟蹤定位算法。該算法根據已獲得的估計信息直接對各系統定位信息和誤差協方差進行交互，并根據多系統并行濾波中的新息及其方差不斷更新系統概率，最后按照系統概率將各系統的狀態估計加權融合輸出。仿真結果表明IMS算法能夠獲得較好的性能。

2　多系統跟蹤定位建模

采用多個系統對目標進行跟蹤定位，目標運動狀態方程和觀測方程可以表示為

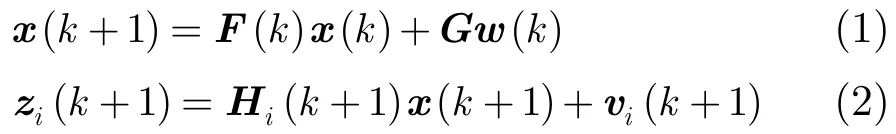
假設機動目標運動過程中，用多個系統對其進行觀測跟蹤，系統間的轉移概率可以用一階馬爾科夫鏈表示[15]：

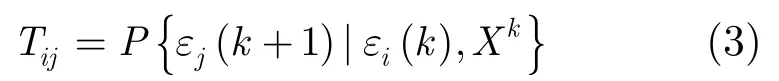
3交互式多系統跟蹤定位算法（IMS）

3.1 多系統交互

在多系統并行濾波前，首先根據已有估計新息對系統定位信息進行交互。當k +1時刻系統j有效時，系統間交互概率為

基于以上計算獲得的交互概率，對k +1時刻各系統的定位信息和噪聲方差進行交互，作為后續并行濾波器的輸入：

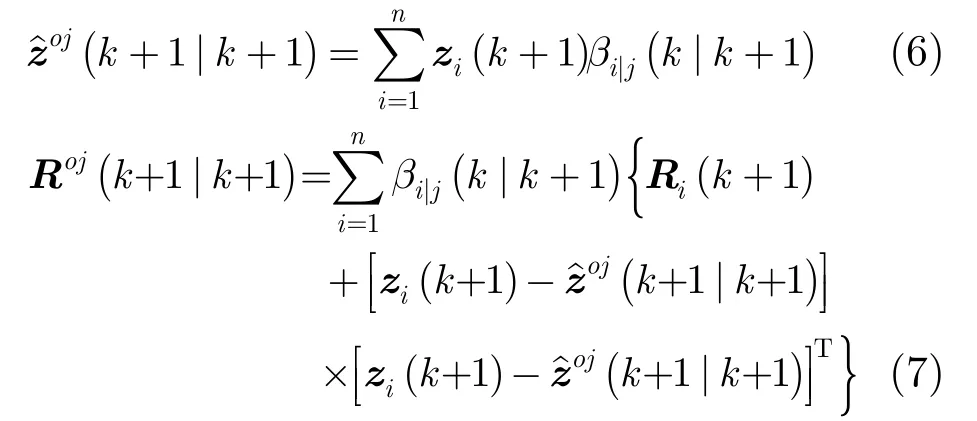
3.2 多系統并行濾波

以多系統交互后的定位信息和噪聲方差為輸入進行并行濾波。簡單起見，此處采用較為簡便的卡爾曼濾波器(Kalman Filter，KF)進行濾波估計。

預測值計算：

其中G為噪聲傳遞矩陣，k +1時刻系統j的新息及方差為

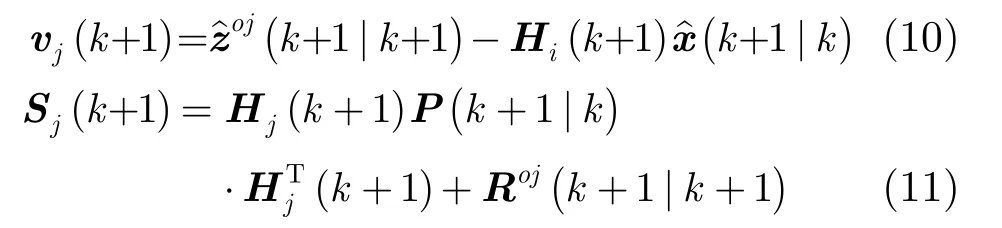
增益因子計算：

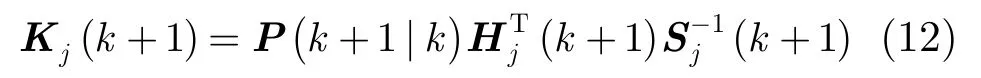
狀態及其方差估計：

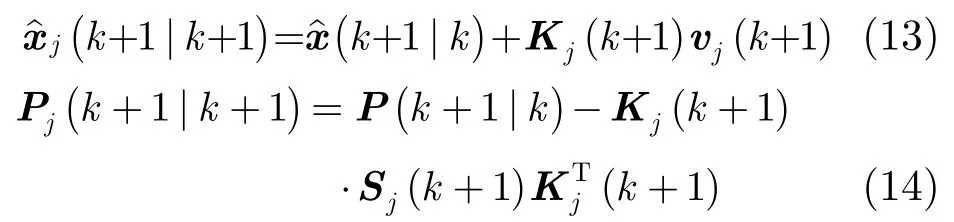
3.3 系統概率更新

每一采樣時刻根據濾波所得新息及其方差對系統概率進行更新，k +1時刻系統j的后驗概率為

3.4 多系統融合輸出

在系統概率更新的基礎上，將各系統濾波結果按照貝葉斯條件概率進行融合，得到最終的跟蹤定位結果估計值和估計誤差協方差：

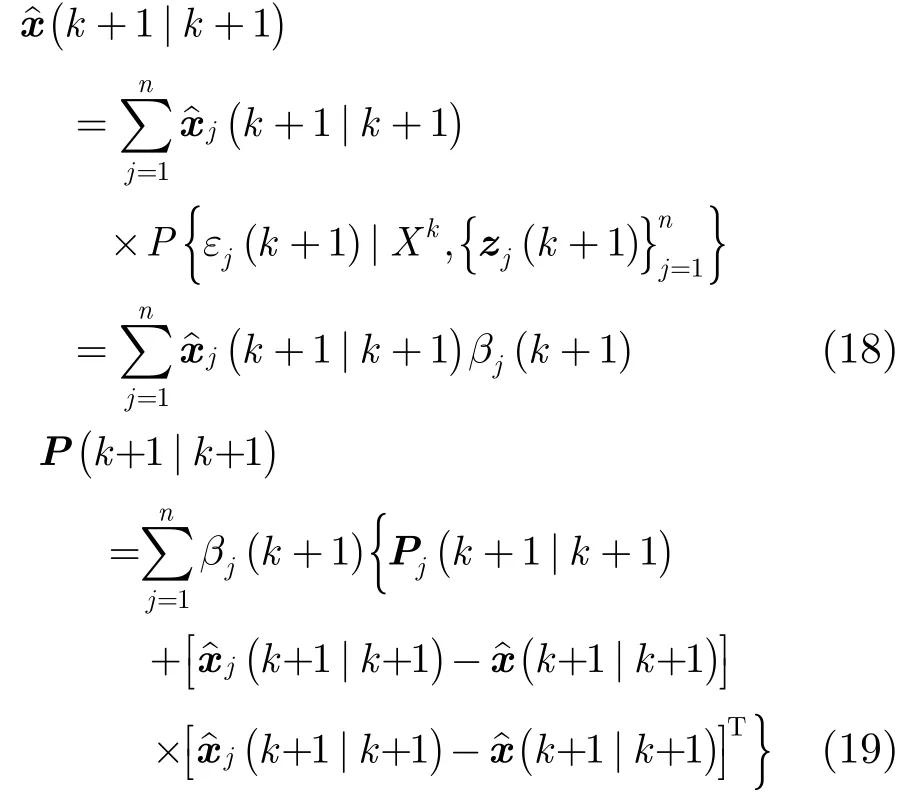
4　仿真分析

為了驗證本文所提出的IMS算法的有效性，分別對本文提出的IMS算法和文獻[13]，文獻[14]中提出的多傳感器交互式算法(IMSF)進行仿真，并對性能進行對比分析。

仿真中定位目標的初始位置及速度為(-104m，-104m)和(30 m/s，0 m/s)，前1500 s做勻速直線運動，然后以加速度(0.1 m/s2，0.1 m/s2)做1500 s的勻加速運動。仿真中采樣周期T =1 s，設置3個系統對目標進行跟蹤定位，觀測矩陣，相應的觀測誤差如表1所示。

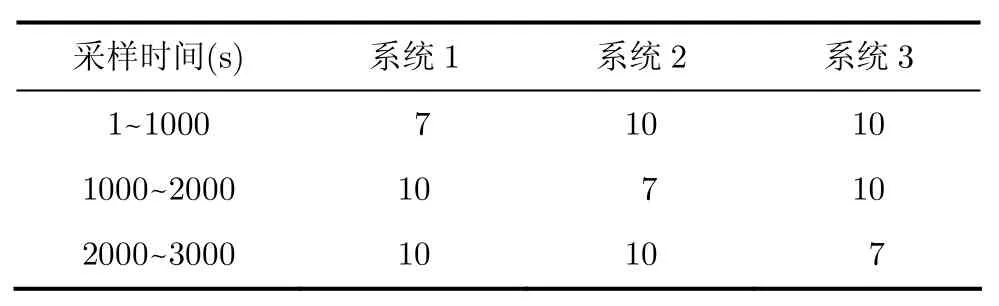
表1　3個定位系統的定位誤差（m）

則3個系統觀測噪聲協方差矩陣為

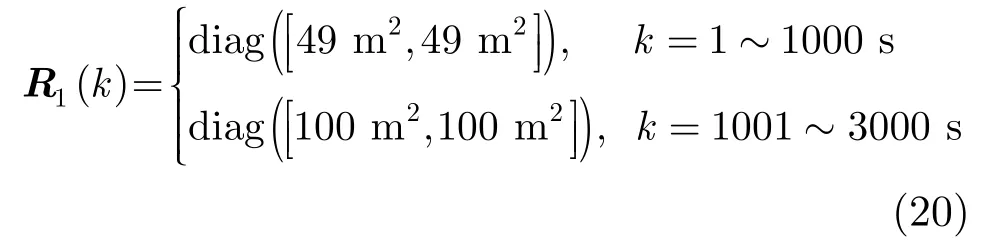
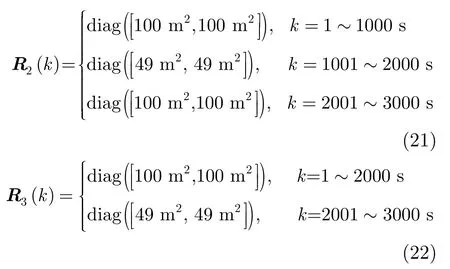
系統間切換的一階馬爾科夫轉移概率矩陣為

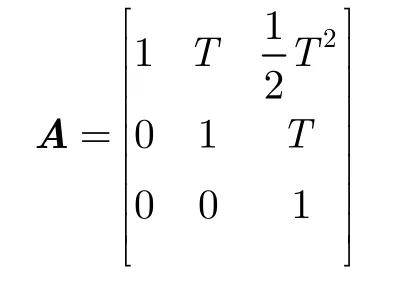
誤差傳遞矩陣為

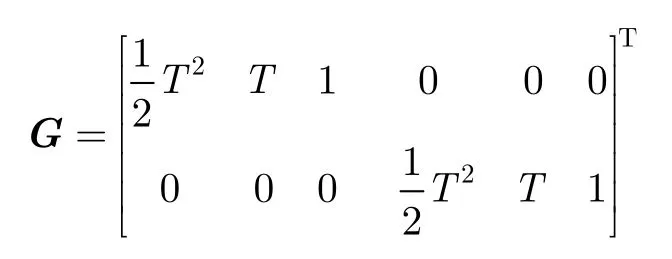
運動過程中的加速度噪聲標準差wx=wy=，對應的協方差矩陣進行3000次Monte Carlo仿真，得到兩種算法的跟蹤性能結果，其中圖1和圖2為截取50個采樣點獲得的目標位置和速度RMSE曲線，圖3和圖4為3000個采樣點統計獲得的RMSE誤差統計曲線，其中虛線為IMSF算法的結果，實線為IMS算法的結果。

從圖1和圖2可知在跟蹤定位過程中，本文所提出的IMS算法能夠將位置誤差和速度誤差控制在更小的范圍之內，獲得更好的跟蹤定位性能。圖3和圖4進一步從統計角度證實了這一結論，從圖中可以看出，相同的誤差概率下IMS算法的誤差更小。

圖5為IMS算法下三系統在整個仿真過程中的系統概率變化情況。仿真中動態調整三系統定位誤差均值的大小，使三系統的定位性能交替變化，性能相差30%。從圖中可以看出本文所提出的IMS算法能夠很好地根據定位系統的性能變化快速調整系統概率，使得任何時候性能越好的系統所占的概率越大。但是系統的切換仍然存在一定的滯后性，這是由于系統之間的轉移概率是人為先驗確定的，并沒有利用相關信息進行實時調整，根據文獻[5]的論述可知，采用先驗確定的轉移概率是系統切換與未切換情況下的一種折中。

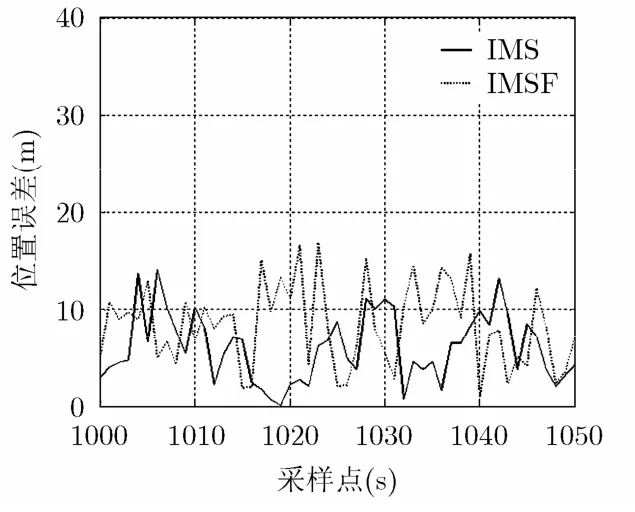
圖1　位置誤差RMSE曲線

圖2　速度誤差RMSE曲線

圖3　位置誤差RMSE概率統計

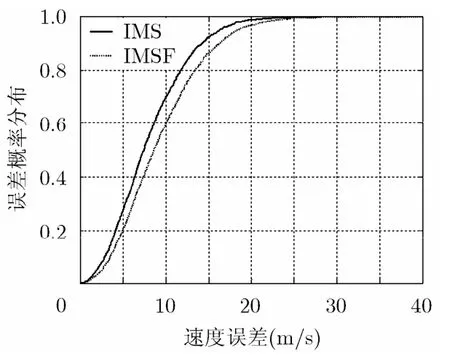
圖4　位置誤差RMSE概率統計

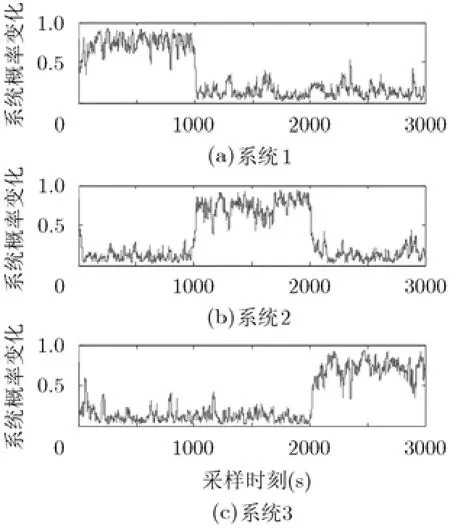
圖5　IMS算法系統概率

5　結束語

本文借鑒交互式多模型的思想提出一種多系統交互式跟蹤定位算法，實現多系統間定位信息和誤差的直接交互。仿真結果表明與已有的多傳感器交互式定位算法相比，該算法能夠根據系統性能變化及時調整系統概率，有效提高目標跟蹤定位性能。但由于系統之間的切換概率是人為先驗確定的，當系統性能快速切變時存在一定的延遲，需要進一步改進。

參考文獻

[1]BLOM H A P and BAR-SHALOM Y.The interacting multiple model algorithm for systems with Markovian switching coefficients[J].IEEE Transactions on Automatic Control，1988，AC-33(8):780-783.doi:10.1109/9.1299

[2]秦雷，李君龍，周荻.基于交互式多模型算法跟蹤臨近空間目標[J].系統工程與電子技術，2014，36(7):1243-1249.doi:10.3969/j.issn.1001-506X.2014.07.04.QIN Lei，LI Junlong，and ZHOU Di.Tracking for near space target based on IMM algorithm[J].Systems Engineering and Electronics[J].2014，36(7):1243-1249.doi:10.3969/j.issn.1001-506X.2014.07.04.

[3]SUN Can，XING Jianping，LIANG Haozhe，et al.S-IMM:Switched IMM algorithm for maneuvering target tracking[J].Journal of Convergence Information Technology，2012，14(7):461-468.

[4]陳亮，楊峻巍，舒曉菂.基于K-L信息因子的變結構多模型算法模型集自適應研究[J].系統工程與電子技術，2013，35(12):2459-2466.doi:10.3969/j.issn.1001-506X.2013.12.03.CHEN Liang，YANG Junwei，and SHU Xiaodi.Model-set adaptive algorithm of variable structure multiple-model based on K-L criterion[J].Systems Engineering and Electronics，2013，35(12):2459-2466.doi:10.3969/j.issn.1001-506X.2013.12.03.

[5]羅笑冰，王宏強，黎湘.模型轉移概率自適應的交互式多模型跟蹤算法[J].電子與信息學報，2005，27(10):1539-1541.LUO Xiaobing，WANG Hongqiang，and LI Xiang.Interacting multiple model algorithm with adaptive markov transition probabilities[J].Journal of Electronics ＆ Information Technology，2005，27(10):1539-1541.

[6]周衛東，蔡佳楠，孫龍.具有最有模型傳遞矩陣的交互式多模型算法[J].哈爾濱工業大學學報，2014，46(11):101-106.ZHOU Weidong，CAI Jianan，and SUN Long.Interacting multiple model with optimal mode transition matrix[J].Journal of Harbin Institute of Technology，2014，46(11):101-106.

[7]劉貴喜，高恩克，范春宇.改進的交互式多模型粒子濾波跟蹤算法[J].電子與信息學報，2007，29(12):2810-2813.LIU Guixi，GAO Enke，and FAN Chunyu.Tracking algorithms based on improved interacting multiple model particle filter[J].Journal of Electronics ＆ Information Technology，2007，29(12):2810-2813.

[8]劉妹琴，湯曉芳，鄭世友，等.基于RUKF-IMM的非線性系統濾波[J].華中科技大學學報(自然科學版)，2013，41(5):57-63.LIU Meiqin，TANG Xiaofang，ZHENG Shiyou，et al.Filtering of nonlinear systems with measurement loss by RUKFIMM[J].Journal of Huazhong University of Science and Technology(Natural Science Edition)，2013，41(5):57-63.

[9]周衛東，劉萌萌，楊永江.基于多傳感器信息融合理論的交互式多模型算法[J].華南理工大學學報(自然科學版)，2014，42(9):82-89.doi:10.3969/j.issn.1000-565X.2014.09.015.ZHOU Weidong，LIU Mengmeng，and YANG Yongjiang.An improved interacting multiple model algorithm based on multi-sensor information fusion theory[J].Journal of South China University of Technology(Natural Science Edition)，2014，42(9):82-89.doi:10.3969/j.issn.1000-565X.2014.09.015.

[10]吳楠，王旭東，胡晴晴，等.基于多LED的高精度室內可見光定位方法[J].電子與信息學報，2015，37(3):727-732.doi:1011999/JEIT140725.WU Nan，WANG Xudong，HU Qingqing，et al.Multiple LED based high accuracy indoor visible light positioning scheme[J].Journal of Electronics ＆ Information Technology，2015，37(3):727-732.doi:1011999/JEIT140725.

[11]谷陽，宋千，李楊寰，等.基于慣性鞋載傳感器的人員自主定位粒子濾波方法[J].電子與信息學報，2015，37(2):484-488.doi:10.11999/JEIT140362.GU Yang，SONG Qian，LI Yanghuan，et al.A particle filter method for pedestrian navigation using foot-mounted inertial sensors[J].Journal of Electronics ＆ Information Technology，2015，37(2):484-488.doi:10.11999/JEIT140362.

[12]何堅，萬志江，劉金偉.基于電源線和位置指紋的室內定位技術[J].電子與信息學報，2014，36(12):2902-2908.doi:10.3724 /SP.J.1146.2013.02022 HE Jian，WAN Zhijiang，and LIU Jinwei.Indoor positioning technology based on powerline and location fingerprint[J].Journal of Electronics ＆ Information Technology，2014，36(12):2902-2908.doi:10.3724/SP.J.1146.2013.02022.

[13]劉志剛，汪晉寬.多傳感器交互濾波算法[J].電子學報，2012，40(4):724-728 doi:10.3969/j.issn.0372-2112.2012.04.016.LIU Zhigang and WANG Jinkuan.Interacting multiple sensor filter for sensor networks[J].Acta Electronica Sinica,2012，40(4):724-728.doi:10.3969/j.issn.0372-2112.2012.04.016.

[14]LIU Zhigang，WANG Jinkuan，and XUE Yanbo.Interacting multiple sensor filter[J].Signal Processing，2012，92(9):2180-2186.

[15]BAR-SHALOM Y and LI X R.Multitarget-Multisensor Tracking:Principles and Techniques[M].Los Angeles，CA，US，Artech House，Inc.，1995:187-277.

張曉光：男，1983年生，助理研究員，研究方向為衛星導航及傳感器導航、制導與控制.

魏東巖：男，1985年生，副研究員，研究方向為衛星導航及傳感器導航、制導與控制.

徐穎：女1983年生，研究員，研究方向為衛星導航及信號體制.

Interacting Multiple System Tracking Algorithm

ZHANG XiaoguangWEI DongyanXU YingYUAN Hong
(Academy of Opto-Electronics，Chinese Academy of Sciences，Beijing 100094，China)

Abstract:Interacting algorithm is widely used in multi-model target tracking，but it is rarely used in multi-system target tracking.In this paper，the interacting idea is used as a reference，and an interacting multi-system tracking algorithm is proposed.The direct interaction between systems is finished based on their former state estimation.Then system probabilities are updated using innovation and its covariance from the parallel filters.Finally，weighted fusing results are achieved on the updated probabilities.The simulation result of tracking a maneuvering target shows that system probability can be adjusted based on its performance immediately，and the tracking performance can be improved effectively.

Key words:Multi-system tracking; Interacting; System probability

基金項目：中國科學院光電研究院創新項目(Y40802A1BY)

*通信作者：張曉光zxg@aoe.ac.cn

收稿日期：2015-05-11；改回日期：2015-11-04；網絡出版：2016-01-04

DOI:10.11999/JEIT150543

中圖分類號：TP391

文獻標識碼：A

文章編號：1009-5896(2016)02-0389-05

Foundation Item:The Innovation Program of Academy of Opto-Electronics，Chinese Academy of Sciences(Y40B02A1BY)