厘清脈絡 建構聯系 感悟思想
——《平面圖形的面積總復習》教學設計與思考

朱元華

【教學過程】

一、明確任務，自主整理脈絡

1.課前談話，引出課題。

小學階段我們學習了哪些平面圖形？這些圖形有什么特征？今天我們一起復習它們的面積計算。出示課題：平面圖形的面積總復習。

2.回憶面積公式及推導方法。

它們的面積計算方法分別是怎樣的？這些面積公式是怎么推導出來的？選擇其中的一個進行說明。

3.自主整理，初步感知聯系。

你能用一幅簡潔的圖示表示下列面積公式之間的聯系嗎？請在練習紙上畫一畫。

自主整理要求：（1）想一想：這些公式是怎樣推導出來的？（2）畫一畫：把它們之間的聯系用簡要的圖示表示出來。

二、小組交流，完善知識結構

1.小組交流，完善結構圖。

2.教師巡視，適時指導。

3.匯報反饋。

（1）你是怎樣整理的？為什么？請說明理由。

（2）比較和辨析不同的整理成果。

（3）初步形成圖形面積公式之間的知識結構圖。

三、討論聯系，互通知識網絡

1.觀察結構圖，你發現了什么。

我們學習知識的先后順序是有講究的，如果把這個結構圖逆時針旋轉90度，就形成了一棵知識樹，正如樹一樣，從樹干到樹枝并不是隨意生長的。

（1）從下往上看，根據長方形的面積公式可以推導出其他圖形的面積公式。

（2）從上往下看，我們在探討一種新的圖形面積計算時，都是把它轉化成已經學過的圖形來研究的。

（3）小結“轉化”的數學思想，把未知轉化為已知，這是研究新問題常用的辦法。

2.全班討論：哪個圖形的面積公式可以推導其他圖形的面積公式？

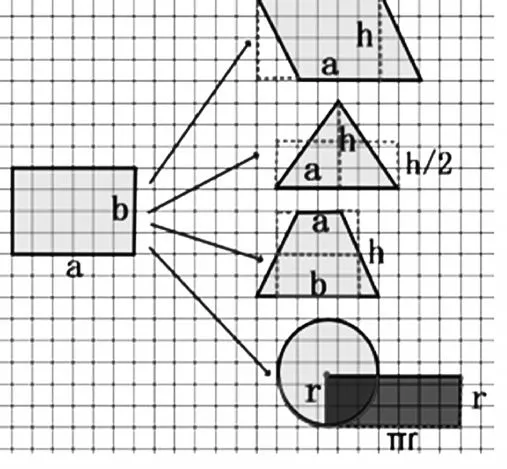
（1）以長方形為基礎共構知識網絡圖。

討論一：為什么我們要先學長方形的面積公式？

這是因為面積單位是正方形，而長方形最方便用面積單位擺一擺，數格子得到面積。

面積單位都是以邊長是1厘米、1分米、1米、100米，甚至1000米的正方形。那么什么叫面積呢？

面積就是物體表面或平面圖形的大小。如果把這些平面圖形的面積計算方法看作是一棵大樹的話，面積的定義就是這棵樹的樹根，是研究這些所有平面圖形的面積計算方法的基礎。長方形的面積就是這棵樹的樹干。

討論二：你能用長方形的面積公式推導出其他所有的公式嗎？

學生匯報，教師課件演示。

（2）以梯形為主線構建知識網絡圖。

想象：上底和下底的和為10，高為4的梯形有哪些形狀？

通過想象梯形的形狀，滲透運用“運動”的視角，溝通以梯形的面積公式為主線的知識網絡，發展學生空間觀念的同時，感悟圖形面積公式的共通性。

誰能用梯形的面積公式變換出其他所有圖形的面積公式？

預設課件呈現：

當上底為0時，就變成三角形；當上下底一樣時，就變成平行四邊形；當上下底相等并垂直，就成了長方形等。通過進一步溝通，加強梯形面積公式與其他面積公式的聯系。

3.環節小結。

根據學生發言，提煉出課堂結構“自主整理——小組交流——討論聯系——分層練習”，我們是“先理再練”的復習形式，接下去我們要運用所學知識去解決問題。

四、分層練習，全面內化提升

A組：

一個三角形底45厘米，高20厘米，它的面積是（），一個與它面積和高都相等的梯形，上底為15厘米，下底為（）厘米。

B組：

你能將一個上底5厘米，下底16厘米，高10厘米的梯形平均分成面積相等的三等份嗎？請分一分、畫一畫。

C組：

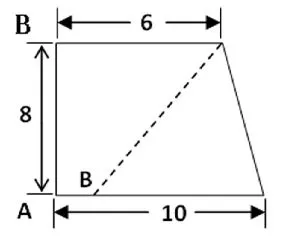
如果用虛線將梯形分成面積相等的兩部分,那么AB的長度是多少？

【課后思考】

自主梳理，構建網絡——開展有效復習的關鍵點

復習課是幫助學生梳理和重新組織知識，使之系統化、結構化，完善認知結構的過程。

在《平面圖形的面積總復習》一課中，注重學生的自主學習，多元表征知識結構，通過“自主整理——小組交流——全班討論”的教學環節，讓學生自主參與知識的整理，在合作交流學習中，理清了各種平面圖形面積公式的內部聯系，形成了多元化的知識結構網，充分發揮了學生的積極能動性。

在自主整理梳理的過程中，回憶公式的推導過程，進一步深化“轉化”思想的感悟，不僅達成對知識的理解，而且不斷積累有效的復習經驗和學習方法，真正達成“理而通”的復習效果。

分層練習，差異發展——找準有效復習的著力點

復習課應重視錯題歸類，分層練習，突出重點，實施有針對性的差異化學習。注重分層練習，實現差異化的發展

在《平面圖形的總復習》一課中，根據學生的錯題情況，總結出學生存在的四大問題：（1）死套公式；（2）不善變通；（3）缺乏聯系；（4）方法單一。針對這些問題，練習設計A、B、C三組練習題。通過分層練習，實現差異化的教學，取得良好的效果。

感悟思想，拓展能力——重視有效復習的延伸點

復習課也應該考慮不同層次學生的要求，可以有所延伸和拓展，做到“下要保底，上不封頂”。這樣才能做到溫故而知新，促進學生可持續的發展。如在本課教學時，課堂小結后，進行了一些拓展性學習。

師：你們還想研究什么圖形的面積計算方法？

生：我想研究多邊形的面積計算方法。

師：那我們就以正五邊形為例，想一想我們可以怎樣研究？

生：用轉化思想，把它分成我們學過的圖形進行研究。

生：可以從正多邊形的中心出發，將它分成若干個三角形。

師：大家明白這位同學的意思嗎？能想象出是怎么分的嗎？（課件演示）

師：請同學們繼續想下去，隨著邊數變多，圖形逐漸變成什么圖呢？

生：啊！（恍然大悟）變成圓形，圓可以看作正無數邊形。

生：看來圓的面積也可以用三角形的面積公式推導出來。

師：怎么推導呢？

生：圓的周長相當于無數個三角形底之和，圓的半徑相當于三角形的高，三角形的面積=底×高÷2，那么圓面積=圓周長×半徑÷2。