由此及彼 由個到類
——以“問題解決”的教學為例張

福建省廈門市湖里第二實驗小學 張碧玉

由此及彼 由個到類
——以“問題解決”的教學為例張

福建省廈門市湖里第二實驗小學 張碧玉

在數(shù)學問題教學的實踐中，往往需要引導學生進行由此及彼、由個到類的數(shù)學思考，進而發(fā)展學習者轉(zhuǎn)化與類化的能力。這些能力能發(fā)展學習者的數(shù)學素養(yǎng)，讓學習者因?qū)W數(shù)學而智慧。

小學數(shù)學 問題解決 轉(zhuǎn)化類化

眾所周知，數(shù)學使人聰明，學好數(shù)學能更簡潔、準確、快速地解決問題，這種能力亦或稱之為素養(yǎng)的東西如何通過數(shù)學學習得以培養(yǎng)起來，值得每一位數(shù)學教育工作者的深思與踐行。筆者發(fā)現(xiàn)：在數(shù)學問題教學的實踐中，往往需要引導學生進行由此及彼、由個到類的數(shù)學思考，進而發(fā)展學習者轉(zhuǎn)化與類化的能力。這些能力的培養(yǎng)，反過來又能促進解決問題的水平與能力的提升，同時發(fā)展學習者的數(shù)學素養(yǎng)，讓學習者因?qū)W數(shù)學而智慧。

一、由此及彼，發(fā)展學生的轉(zhuǎn)化能力

轉(zhuǎn)化是指將未知的、陌生的、復(fù)雜的問題通過演繹歸納轉(zhuǎn)化為已知的、熟悉的、簡單的問題,從而使問題得以順利解決的一種數(shù)學思想方法。發(fā)展學生的轉(zhuǎn)化能力，可以讓學生自主建構(gòu)更完整更系統(tǒng)的知識體系。因此，在問題解決教學中，教師應(yīng)當在轉(zhuǎn)化的素材與時機上下功夫，讓學生在恰當?shù)臅r機運用適當?shù)乃夭淖龊棉D(zhuǎn)化的文章。

1.活用轉(zhuǎn)化的素材。轉(zhuǎn)化雖無處不在，但能把素材進行巧妙的利用，離不開老師對教材的深入挖掘和把握。特級教師俞正強執(zhí)教的《植樹問題》一課就是很好的典范。在傳統(tǒng)的教學中，我們往往是直接出示植樹新問題，引導學生通過畫線段圖從而得到“棵樹比段數(shù)多1”的辦法。但在俞老師的課堂上，他卻在新舊知識的聯(lián)結(jié)點上，巧妙運用轉(zhuǎn)化，化新為舊，以舊引新。

課一開始，俞老師在黑板上出示一道題：20米，平均每5米分一段，共分幾段？這是一道典型的平均分問題，學生們很快解答為：20÷5=4（段）。

緊接著，俞老師出示了第二道題：20米路，每5米栽一棵樹，共栽幾棵樹？

生1：應(yīng)該還是用除法，20÷5=4。

師：有不同意見嗎？

生2：我認為應(yīng)該是要種5棵樹。

師：為什么？

生2：因為每5米一棵樹，而剛開始的時候就要先種一棵樹，所以是種5棵樹。

師：我們算出來明明是4棵，他偏偏說是5棵，誰懂他的意思？

生3：是不是就是從0米開始就要先種一棵？

這時俞老師利用線段圖畫一畫，引導學生感受“5棵樹”的由來。

師：這兩道題有沒不一樣？不一樣在哪里？

生：一個問分幾段，另一個問種幾棵。

師：幾段和幾棵有什么不一樣嗎？

生：段是兩個中間的一個單位，棵是以個為單位的。

師：平均分是一段一段分的，但種樹的時候，是種在段上的還是種在哪里的？

生：段與段之間的點上。

師：對！種樹是種在點上的，兩者的區(qū)別就在這兒……

數(shù)學中每一個新知識幾乎都是在舊知識的某一連接點上生長起來的，從教學片段中可以發(fā)現(xiàn)，俞老師巧妙地從除法平均分入手，先解決一道平均分“舊問題”，再試著解決植樹“新問題”，制造出“我們算出來明明是4棵，他偏偏說是5棵，這是怎么回事”的認知沖突，再深入分析“這兩道題有沒不一樣？不一樣在哪里”，在尋找植樹問題與平均分問題之間的異同點中，感受新舊知識的緊密聯(lián)系，也讓學生對新生事物自然而然產(chǎn)生親切感。

2.巧用轉(zhuǎn)化的時機。教學實踐表明：同樣的素材會因不同的時機選擇而產(chǎn)生迥然不同的教學效果。因此，教學中老師還要善于把握好轉(zhuǎn)化的時機。例如，在執(zhí)教《加法交換律》一課時，在學生認識了加法交換律后，老師問到：加法交換律我們以前見過嗎？孩子們就想：這不是今天才學習的新知識嗎，我們哪里有見過呢？老師出示下圖，并故作神秘地說：我們不僅見過，我們還用過呢。不信呀，你們瞧！

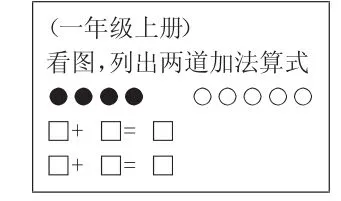
讓學生情不自禁地感嘆到：原來我們早就認識這個新朋友了，數(shù)學知識原來是這樣的緊密聯(lián)系。

這個轉(zhuǎn)化的素材其實也可以前置于課的開始，然而，置于課的開始將大大地削弱本課的探究性。而此時“回馬一槍”將新知與舊知聯(lián)系起來，引導學生由此及彼，對于學生建立系統(tǒng)的知識結(jié)構(gòu)是很有好處的，并且也讓學生對轉(zhuǎn)化思想的體驗更深刻更真切。

綜上所述，在不斷地由此及彼的轉(zhuǎn)化中，教師通過對教材進行深入細致的挖掘和運用，把看似無關(guān)聯(lián)的知識點在恰當?shù)臅r機進行巧妙的轉(zhuǎn)化。學生一方面會發(fā)現(xiàn)數(shù)學知識不是割裂的知識碎片，而是充滿聯(lián)系的整體，這對于他們利用聯(lián)系的方法學習數(shù)學是大有幫助的。同時培養(yǎng)起他們一種普遍聯(lián)系的哲學眼光；另一方面，在廣泛的轉(zhuǎn)化的學習經(jīng)驗的積累中，學生自然而然地可以在轉(zhuǎn)化中學會轉(zhuǎn)化，發(fā)展轉(zhuǎn)化的能力。

二、由個到類，發(fā)展學生的類化能力

類化，就是讓學生通過解決一個問題進而學會解決這一類的問題，從而借助事情的共同特征去認識事物，創(chuàng)造事物。有了類化能力，不僅能形成良好的認知結(jié)構(gòu)，建立數(shù)學模型，還能發(fā)展創(chuàng)新思維，提升學習品質(zhì)。具體地，在數(shù)學解決問題中應(yīng)當注重引導學生敢于聯(lián)想、善于聯(lián)想以培養(yǎng)學生的類化能力。

1.引導學生敢于聯(lián)想。數(shù)學上的聯(lián)想往往表現(xiàn)為一種想象，誠如愛因斯坦所說的：“想象力比知識更重要，因為知識是有限的，而想象力概括著世界上的一切 ，推動著進步，并且是知識進化的源泉。”在解決問題的教學中，教師引導學生大膽聯(lián)想，往往可以突破“一個題”的羈絆，而將目光與思考鎖定到“一類題”共同特征上。

在俞正強老師執(zhí)教的《植樹問題》中就有這樣一個引發(fā)學生聯(lián)想的片段：

師：植樹人把樹植在點上，想想看，還有什么人做什么事也把它做在點上的？

在俞老師循循善誘下，學生們放飛思維，舉出了很多生活中“種”在“點”上的例子，如：桌上每隔幾分米放一個水杯，這里水杯是“樹”；建筑工人每隔幾米打地樁，這時地樁成了“樹”；街上每隔幾米豎一個路燈，路燈成了“樹”；高速公路每隔幾米設(shè)置一個服務(wù)區(qū)，服務(wù)區(qū)成了“樹”；每節(jié)課的課間放一首音樂，這音樂也成了“樹”。俞老師甚至讓孩子們思考：美國每隔五年選總統(tǒng)，總統(tǒng)是不是“樹”？這個大膽問話，可把孩子們難住了，總統(tǒng)怎么成了樹？可每隔五年的規(guī)律就是平均分，總統(tǒng)居然真的是“樹”。多么大膽的聯(lián)想啊！不僅讓學生看到了一棵樹，更是看到了一片的“數(shù)學問題”的樹林。

這樣一種打開學生視界的教學，讓學生逐漸地學會由個到類地思考問題，也讓學生的思維更開放、更自由、更無拘束，由此，與其說打開的是眼光中的視界，毋寧說打開的是學生思維的天地。

2.引導學生善于聯(lián)想。大膽地聯(lián)想是意識層面的，只有意識上的“敢于聯(lián)想”顯然是不夠的，在具體的數(shù)學問題解決的教學中，教師還應(yīng)當引導學生學會聯(lián)想的方法，從而善于聯(lián)想。只有這樣，有了主動聯(lián)想的意識，再加上有了聯(lián)想的方法，學生才能真正在問題解決中自覺運用聯(lián)想的方法，從而在不斷積累的聯(lián)想的經(jīng)驗與體驗中學會由個到類地數(shù)學思考。

在《用字母代表數(shù)》一課中，老師設(shè)計了這樣一道搶答題：

①蝸牛每天爬3米，x天爬（ ）米。

②一朵百合花3元，x朵百合花（ ）元。

③阿姨每天做3面紅旗，x天做（ ）面紅旗。

師：你發(fā)現(xiàn)了什么？

生：答案都是3x

師：3x給我們講述了不同的數(shù)學故事，它還可以講什么故事呢？你來試試看。于是，同學們打開了思維的大門，暢所欲言地講述他們對3x這道式子在生活中的運用。這樣的練習設(shè)計，不僅讓孩子們用數(shù)學的眼光去發(fā)現(xiàn)生活中的數(shù)學問題，更讓學生進一步體會，現(xiàn)實生活中的看似許多不同事件，其實都蘊含著相同的數(shù)量關(guān)系或者數(shù)學意義。

綜上所述，解決問題的教學不是為了一個題的教學，而是為了一類題的領(lǐng)悟。學生對一類題的領(lǐng)悟不可能也不應(yīng)當建立在完成一類題的訓練之后，教師要做的是讓學生從一個題中看到一類題，那種就題講題的教學是讓學生只見樹木不見森林的教學，是低效的教學，更是制約學生思維能力發(fā)展的教學。更恰當?shù)淖龇☉?yīng)當是引導學生大膽聯(lián)想，“舉一隅而以三隅反”，進而在不斷的經(jīng)驗積累中發(fā)展“由個到類”的數(shù)學思考。同時在廣泛的類化的學習經(jīng)驗的積累中，在類化中學會類化，發(fā)展類化的能力。