基于平方根CKF的多傳感器序貫式融合跟蹤算法

劉　華, 吳　文, 王世元

(1. 南京理工大學近程高速目標探測技術國防重點學科實驗室, 江蘇 南京 210094;

2. 西南大學電子信息工程學院, 重慶 400715)

?

基于平方根CKF的多傳感器序貫式融合跟蹤算法

劉華1, 吳文1, 王世元2

(1. 南京理工大學近程高速目標探測技術國防重點學科實驗室, 江蘇 南京 210094;

2. 西南大學電子信息工程學院, 重慶 400715)

摘要：為了提高非線性序貫式融合跟蹤算法的精度,提出了基于平方根容積卡爾曼濾波器的多傳感器序貫式融合跟蹤算法。該算法使用三階容積數值積分原則計算非線性過程的均值和方差,克服了擴展卡爾曼濾波器存在的濾波精度低及平方根無跡卡爾曼濾波器存在的參數復雜的缺點。同時，在濾波遞歸過程中以協方差平方根矩陣代替協方差矩陣,這樣確保了濾波算法的數值穩定性,提高了跟蹤的精度。最后用已知彈道系數的再入段彈道跟蹤模型對所提算法的性能進行仿真測試。仿真結果表明,所提算法具有很好的跟蹤性能,是一種有效的非線性序貫式融合跟蹤算法。

關鍵詞：多傳感器; 序貫式融合; 平方根容積卡爾曼濾波器; 再入段

0引言

多傳感器非線性融合跟蹤算法是一種將多個相同或者不同類型傳感器所提供的觀測信息加以融合形成統一的狀態估計的算法,它能提高單傳感器目標跟蹤算法的準確性,因此得到了學者的廣泛關注。目前已有許多非線性融合算法,主要有集中式融合算法[1-2]和分布式融合算法[3-4]。但這兩種算法都是在獲取所有傳感器的測量值后才能對系統狀態進行融合估計,因此對于實時性要求很高的系統而言,難以滿足其應用要求。

針對上述兩種融合算法存在的實時性問題,文獻[5]提出了多傳感器非線性序貫式融合算法。該算法先用第一個傳感器的測量值更新系統預測狀態及對應的預測協方差,接著依次用下一個傳感器的測量值更新前一個傳感器更新所得的狀態估計及對應的協方差,最后得到該時刻目標狀態的全局融合估計值及其相應的協方差。文獻[5]所提出的算法不僅在融合精度上與集中式融合算法等價,而且能做到測量值即到達即濾波,具有很好的實時性。但由于文獻[5]的融合算法是基于擴展卡爾曼濾波(extended Kalman filter, EKF)算法的,因此存在EKF算法的一些固有缺點:①需要計算非線性系統的雅克比矩陣,這將導致算法的穩定性降低,甚至會出現發散;②處理強非線性系統時精度會降低。

針對文獻[5]存在的不足,文獻[6-7]分別提出了基于平方根無跡卡爾曼濾波器(square-root unscented Kalman filter, SRUKF)的序貫式融合算法和基于SRUKF的序貫融合粒子濾波算法。由于SRUKF算法能精確地捕獲任何非線性高斯系態的二階矩,因此,與文獻[5]的算法比,基于SRUKF的序貫融合算法有更高的融合精度。但SRUKF算法存在3個可調參數,需選擇適當才能達到良好的濾波效果,而且需要2n+1(n是系統狀態維數)個采樣點,這給工程實踐帶來了一定限制。

文獻[8-9]提出一種基于3自由度球面-徑向容積準則的非線性濾波器,即容積卡爾曼濾波器 (cubature Kalman filter, CKF)。該算法使用一組等權值的容積點集來計算非線性變換后的隨機變量的均值和協方差。與EKF算法相比,該算法具有更優的非線性逼近性能(三階矩)、數值精度以及濾波穩定性。與UKF算法相比,該算法具有實現簡單、運算時間短的特點。該算法一經提出就在導航[10]、目標跟蹤[11-13]、數據融合[14-15]等領域得到廣泛應用。

由于CKF算法在數值計算中存在著噪聲信號和計算誤差等因素,有時會得到負的協方差陣,從而導致CKF出現發散問題。平方根CKF (square-root cubature Kalman filter, SRCKF)[9]算法采用了平方根濾波的思想,確保了協方差陣的非負定性,因此可有效提高CKF濾波的精度和穩定性。本文在結合SRCKF和多傳感器序貫式融合算法優點的基礎上,提出了基于SRCKF的多傳感器非線性序貫式融合跟蹤算法。

本文首先給出了多傳感器非線性系統的系統描述,然后詳細闡述了基于SRCKF算法的多傳感器序貫式融合算法,最后用再入段彈道目標運動模型仿真對比分析了基于EKF、SRUKF、CKF與SRCKF的序貫式融合跟蹤算法的性能。

1系統描述

考慮一個具有加性高斯白噪聲并帶有個傳感器的非線性動態系統

(1)

(2)

式中,E代表均值符號;δtk=1 (t=k;t,k>0); δtk=0(t≠k);Qw與Ri為正定矩陣。

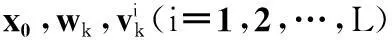
2基于SRCKF的多傳感器序貫式融合算系統描述

2.1SRCKF算法介紹

CKF算法在迭代過程中,由于計算機字長限制而產生的舍入誤差可能導致誤差協方差陣失去對稱性和正定性,致使CKF算法中求平方根操作無法進行,進而導致濾波中斷,影響濾波器的穩定性,而且在每次迭代時都要計算協方差陣的平方根,這需要很大的計算量。為了增加計算過程中的數值穩定性并提高計算效率,Arasaratnam和Haykin在CKF算法的基礎上進一步提出了SRCKF算法。

SRCKF算法的具體流程參見文獻[8]。與CKF算法相比,SRCKF算法具有以下兩個優點:

(1) 在濾波過程中直接以協方差陣的三角分解因子進行遞推更新,而不是協方差陣本身,這樣可降低計算負擔,提高了算法的計算效率;

(2) 保證了協方差陣的非負性,避免了濾波器的發散問題,提高了濾波器的數值穩定性。

2.2基于SRCKF的多傳感器序貫融合算法流程

步驟 1初始化,使用三階容積準則產生2n個基本容積點及對應的權值

(3)

式中,n為系統狀態變量的維數,記n維單位向量為e=[1,0,…,0]T,符號[l]表示對e中元素進行全排列和取反所生成的完全對稱點集,[l]j表示[l]中第j列向量。當n=3時,[l]可表示為

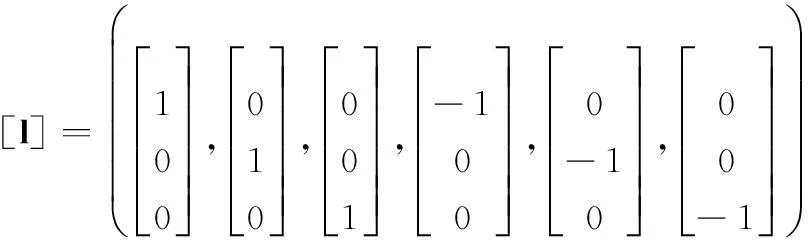
(4)

(5)

(6)

(7)

(8)

(9)

式中,qr{·}表示矩陣的QR分解。

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

綜上所述,可以得到基于SRCKF的多傳感器序貫式融合濾波算法如圖1所示。

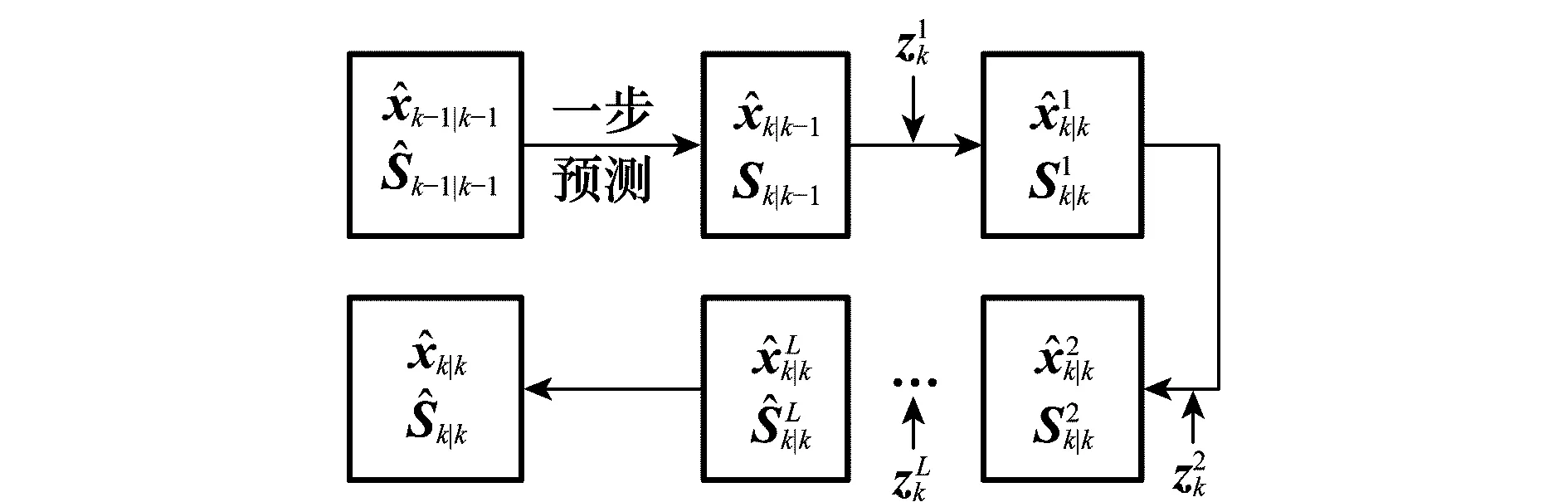
圖1　基于SRCKF的序貫濾波框圖

3再入段彈道目標運動模型和目標測量模型

3.1目標運動模型

再入段導彈距離地面較近,飛行時間較短,可假定地球為平面,并可忽略地球公轉與自轉的影響,且假定目標在再入段時只受到空氣阻力和地球引力的作用,因此可建立再入段彈道的目標運動方程為

(32)

式中,v為運動速度;ρ(z)為目標周圍的大氣密度;β為彈道系數;g是地球引力加速度。大氣密度可建模為與高度z成指數關系的函數,ρ(z)=c1e-c2z,c1與c2均為常數。

對于目標運動方程(32),其相應的離散時間目標運動狀態模型通過歐拉近似得到

(33)

非線性函數D(Sk,β)表達式為

(34)

式中,g=9.81m/s2。矩陣Φ與G分別表示為

fd(Sk-1,β)為空氣阻力對再入目標產生的影響,表達式為

(35)

假設過程噪聲wk是零均值的高斯白噪聲,其協方差矩陣為

(36)

式中,q是過程噪聲強度參數。

3.2目標測量模型

雷達觀測量有兩個,彈道的距離r與俯仰角φ,根據幾何關系,可建立測量方程為

(37)

式中,Mk=[rk,φk]T,rk是目標距離,φk是目標俯仰角,計算公式為

(38)

φk=arctan(zk/xk)+vφ

(39)

雷達測量噪聲vk=[vr,vφ]T為零均值的高斯白噪聲,即vk~N(0,Rk),其協方差矩陣為

(40)

式中,diag{·}表示對角矩陣;σr為雷達的測距誤差標準差;σφ為雷達的俯仰角測量誤差標準差。

4仿真及結果

4.1仿真場景

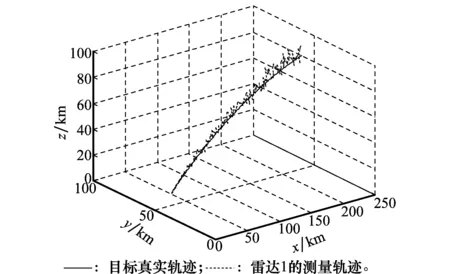
圖2　目標運動軌跡與測量軌跡

設濾波初始方差為P0=diag{[5002, 202, 5002, 202]},濾波初始位置為X0=[232 500,-2 255.2, 88 100,-397.6]T,采樣周期為0.5s,仿真時間為100s,并假定各傳感器均無虛警及漏檢發生,進行200次蒙特卡羅仿真。仿真設備的處理器為AMDAthlon(tm) 64X2DualCoreProcessor4000+,內存為2G。

4.2實驗結果

圖3給出了基于EKF、SRUKF、CKF與SRCKF 4種算法的序貫式融合估計的位置均方根誤差(root mean square error, RMSE)變化曲線,圖4是這4種算法的速度均方根誤差變化曲線。從圖3和圖4中可以看出,基于EKF的序貫式融合算法誤差最大。這是由于EKF算法采用了一階泰勒級數展開,丟棄了高階項,引入了很大的高階截斷誤差,降低了估計精度。從圖中還可得到基于CKF與SRCKF算法的融合估計精度比SRUKF算法的融合估計精度要高,這是由于SRUKF算法僅捕獲非線性高斯系統的二階矩,而CKF與SRCKF算法使用容積數值積分原則對非線性系統方程的均值和方差進行計算,通過此方法能夠達到泰勒展開式的三階精度,因此具有更高的融合估計精度。而SRCKF算法采用了平方根濾波的思想,確保協方差矩陣的正定性,提高了CKF算法的融合估計精度。因此,采用基于SRCKF的序貫融算法能夠提高目標跟蹤精度。

圖3　位置均方根誤差對比

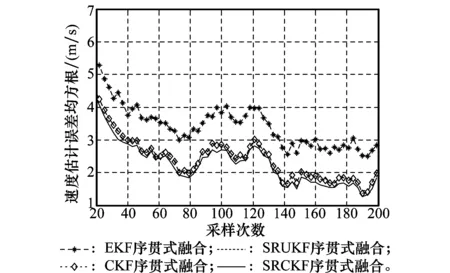
圖4　速度均方根誤差對比

比較算法性能的另一種指標是平均累加均方根誤差(accumulated root mean square error,ARMSE)。下面分別定義位置平均累加均方根誤差ARMSEp與速度平均累加均方根誤差ARMSEv。

(41)

(42)

表1定量地給出了這4種算法的位置與速度的平均累加均方差誤差。從表1可以看出,SRCKF估計精度最高,CKF算法與SRUKF算法次之,EKF算法精度最低。這與圖3和圖4的結果一致。

表1　位置與速度的ARMSE比較

表2給出了4種算法的200次蒙特卡羅仿真的平均運行時間。從表2可看出,SRUKF、CKF和SRCKF算法的計算復雜度均明顯大于EKF算法,而在SRUKF、CKF與SRCKF這3種算法中,SRCKF算法的計算復雜度稍低于另外兩種算法。

表2　算法的運行時間對比

5結論

本文將SRCKF算法與多傳感器序貫式數據融合算法結合,提出了基于SRCKF算法的多傳感器序貫式數據融合算法,并將該算法用于跟蹤彈道系數已知的再入段彈道目標。仿真實驗就估計精度、計算復雜度對本文算法與基于EKF、SRUKF及CKF的多傳感器序貫式融合算法進行了比較,仿真結果證實本文算法的融合精度較高,計算復雜度適中,是一種有效的多傳感器融合跟蹤算法。

參考文獻：

[1] Li X R. Comparison of two measurement fusion methods for Kalman-filter-based multisensor data fusion[J].IEEETrans.onAerospaceandElectronicSystems, 2001, 37(1): 273-280.

[2] Lang H. Centralized and distributed multisensor integration with uncertainties in communication networks[J].IEEETrans.onAerospaceandElectronicSystems, 1991, 27(2): 370-379.

[3] Rao B S, Durrant-whyte H F. Fully decentralized algorithm for multi-sensor Kalman filtering[J].IEEProceedings-DControlTheoryandApplications, 1991, 138(5): 413-420.

[4] Si X H, Li X B, Zhang Y, et al. Multi-sensor fusion target tracking of reentry phase based on square-root unscented Kalman filter[J].SystemsEngineeringandElectronics, 2012, 34(2): 303-306. (司學慧, 李小兵, 張彥, 等. 基于平方根UKF的多傳感器融合再入段目標跟蹤研究[J].系統工程與電子技術, 2012, 34(2): 303-306.)

[5] Wen C L, Lü B, Ge Q B. A data fusion algorithm based on filtering step by step[J].ACTAElectronicaSinica, 2004, 32(8): 1264-1267. (文成林, 呂冰, 葛泉波. 一種基于分步式濾波的數據融合算法[J].電子學報, 2004, 32(8): 1264-1267.)

[6] Guo W Y, Han C Z, Lian F. Multiple-sensor fusion tracking based on square-root unscented Kalman filter[J].JournalofSystemSimulation,2008,20(12):3237-3240.(郭文艷,韓崇昭,連峰.基于平方根UKF的多傳感器融合跟蹤[J].系統仿真學報,2008,20(12):3237-3240.)

[7] Pan B, Feng J F, Li Q, et al. Tracking algorithm for MMW/IR multi-sensors fusion[J].JournalofInfraredandMillimeterWaves,2010,29(3):231-235.(潘勃,馮金富,李騫,等.毫米波/紅外多傳感器融合跟蹤算法研究[J].紅外與毫米波學報,2010,29(3):231-235.)

[8] Arasaratnam I, Haykin S. Cubature Kalman filters[J].IEEETrans.onAutomaticControl, 2009, 54(6): 1254-1269.

[9] Arasaratnam I, Haykin S. Cubature Kalman smoothers[J].Automatica, 2010, 47(10): 2245-2250.

[10] Sun F, Tang L J. INS/GPS integrated navigation filter algorithm based on cubature Kalman filter[J].ControlandDecision, 2012, 27(7): 1032-1036. (孫楓, 唐李軍. 基于cubature Kalman filter的INS/GPS組合導航濾波算法[J].控制與決策, 2012, 27(7): 1032-1036.)

[11] Mu J, Cai Y L. Iterated cubature Kalman filter and its application[J].SystemsEngineeringandElectronics, 2011, 33(7): 1454-1459,1509. (穆靜, 蔡遠利. 迭代容積卡爾曼濾波算法及其應用[J].系統工程與電子技術, 2011, 33(7): 1454-1459,1509.)

[12] Yuan Z J, Zheng N N, Jia X C. The Gauss-Hermit particle filter[J].ActaElectronicSinca,2003,31(7):970-973.(袁澤劍,鄭南寧,賈新春.高斯-厄米特粒子濾波器[J].電子學報,2003,31(7):970-973.)

[13] Lu C G, Feng X X, Zhang D. Pure bearing tracking based on improved cubature Kalman filter[J].SystemsEngineeringandElectronics, 2012, 34(1): 28-33. (鹿傳國, 馮新喜, 張迪. 基于改進容積卡爾曼濾波的純方位目標跟蹤[J].系統工程與電子技術, 2012, 34(1): 28-33.)

[14] Ao Z G, Tang C C, Fu C Q, et al. Multi-sensor adaptive cubature Kalman filter data fusion algorithm[J].ApplicationResearchofComputers,2014,31(5):1312-1315,1331.(敖志剛,唐長春, 付成群, 等. 多傳感器自適應容積卡爾曼濾波融合算法[J].計算機應用研究, 2014, 31(5): 1312-1315,1331.)

[15] Hu Z T,Cao Z W,Li S,et al.Heterogeneous multi-sensor fusion algorithm based on cubature Kalman filter[J].JournalofOptoelectronics·Laser,2014,25(4):697-703.(胡振濤,曹志偉,李松,等.基于容積卡爾曼濾波的異質多傳感器融合算法[J].光電子·激光,2014,25(4):697-703.)

劉華(1980-),男,博士研究生,主要研究方向為非線性濾波、目標跟蹤、多源信息融合。

E-mail: peterliuh@126.com

吳文(1968-),男,研究員,博士,主要研究方向為毫米波制導技術和多模復合制導技術。

E-mail: wuwen@njust.edu.cn

王世元(1980-),男,副教授,博士,主要研究方向為非線性信號處理、自適應濾波器設計、數字通信系統及生物信息學。

E-mail: wsy@swu.edu.cn

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150109.0953.001.html

Multi-sensor sequential fusion tracking algorithm based on

square-root cubature Kalman filter

LIU Hua1, WU Wen1, WANG Shi-yuan2

(1.MinisterialKeyLaboratoryofJGMT,NanjingUniversityofScienceandTechnology,Nanjing210094,China;

2.SchoolofElectronicandInformationEngineering,SouthwestUniversity,Chongqing400715,China)

Abstract:In order to improve the accuracy of the nonlinear sequential fusion algorithm, a new multi-sensor sequential fusion algorithm based on square-root cubature Kalman filter (SRCKF) is proposed. The proposed algorithm uses the third degree spherical-radial cubature rule to calculate the mean and covariance of the nonlinear process, and hence, overcomes the shortcomings of low performance in extended Kalman filter and complex parameters in square-root unscented Kalman filter. Meanwhile, the square-root covariance matrix replaces the covariance matrix in filtering recursion. In this way, the numerical stability of the algorithm is guaranteed and the tracking accuracy is improved. The performance of the proposed algorithm is tested by the reentry trajectory tracking model with known ballistic coefficients. Simulation results show that the proposed algorithm has good tracking performance, and is therefore an effective nonlinear sequential fusion tracking algorithm.

Keywords:multiple sensors; sequential fusion; square-root cubature Kalman filter (SRCKF); reentry phase

作者簡介：

中圖分類號：TP 911

文獻標志碼：A

DOI:10.3969/j.issn.1001-506X.2015.07.05

收稿日期：2014-07-25；修回日期：2014-12-03；網絡優先出版日期：2015-01-09。