倒雙譜的分形維數在故障診斷中的應用

吳文兵，葉福蘭，陳章斌

(福州外語外貿學院，福建福州350018)

0 前言

高階譜由高階累積量進行多次傅里葉變換得來。高階累積量可以消除高斯噪聲，因而可以提取復雜信號中的非高斯信號。與功率譜相比，高階譜同時含有信號的幅度信息和相位信息。高階累積量可以檢測和描述系統的非線性，因而常用于機械系統非線性振動信號的研究［1-2］。高階譜估計主要有以下幾個方面的應用:聲納與雷達處理、多維信號處理、非線性系統分析、生物醫學信號處理、諧波恢復、信號檢測、陳列處理等。由于機械振動信號的非線性、非高斯性和環境中噪聲的高斯性，因而高階譜方法可以去除振動信號中的高斯噪聲，保留其中的非高斯信息，為故障處理提供有力的分析方法。倒譜分析也是機械故障診斷的有效方法，倒譜是將對數功率譜進行反傅立葉變換后得到的，它可以進一步將信道特性和激勵特性有效地分開，但噪聲對倒譜分析的結果具有較大的影響［3-4］。機械設備故障診斷是通過測量機械設備工作狀態的特征信號來識別其狀態的。由于實際測量獲得的信號的切片譜在一定的尺度上具有分形特征，即這些信號切片譜的分形維數會隨著系統狀態的改變而變化，因此分形維數能在一定程度上反映機械設備的運行狀態［5-7］。提取分形維數這一特征量，將有助于對機械設備的正常工作狀態和故障狀態進行診斷和識別。

本文作者將倒譜分析、雙譜分析以及分形理論相結合，針對溢流閥故障信號具有的機械振動信號非線性等共性，提出了通過計算倒雙譜的分形維數進行故障檢測和診斷的方法，并應用到溢流閥的故障診斷中。

1 倒譜與倒雙譜

設{x(n)}為零均值k階平穩隨機過程，功率譜定義為:

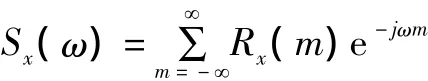
雙譜定義為:

設ω1＝ω2＝ω時，即得到AR雙譜的對角切片Bx(ω，ω)，其中 c3x(τ1，τ2)為三階累積量:

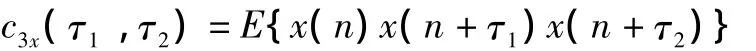
功率譜對數值的逆傅里葉變換稱為倒譜。設信號x(n)的功率譜為Sx(ω)，則倒譜Cx(τ)為

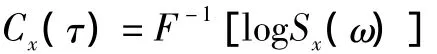
將Bx(ω，ω)代入上式，代替Sx(ω)，即得到倒雙譜。

實際計算中倒雙譜采用下式:

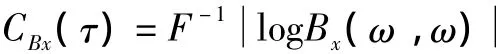
2 容量維與關聯維

按照文獻 ［5］，即采用盒子覆蓋算法來計算功率譜的容量維數。對于Dc維物體:

N(r)∝(1/r)Dc→lim N(r)＝(1/r)Dc

取對數得容量相似維數:

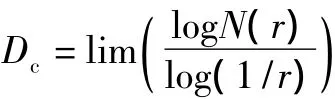
式中:L為線段長度，r為尺子長度，L與r之比為N。

按照文獻［7］，關聯維數可以由實測一維時間序列，利用基于相空間重構的G-P算法直接計算得到。

基于相空間重構，考察m維相空間中的一對相點

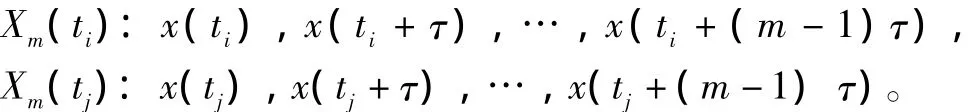
設其距離為εij(m)，則有

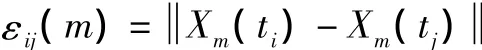
式中:‖·‖為范數，則關聯積分為:

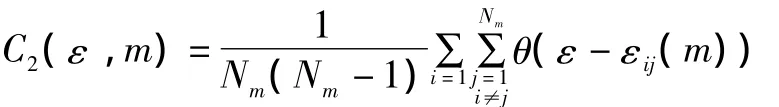
式中:Nm＝n-(m-1)τ為相點數，ε為m維超球半徑 (標度)，θ是Heaviside階躍函數，即有

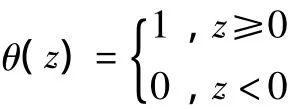
適當選取標度ε，在無標度區內有:

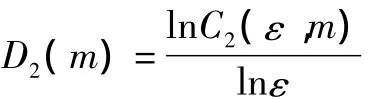
則D2(m)即為關聯維數。

3 數據采集

溢流閥在每個液壓系統中幾乎都要用到，其性能的好壞對整個系統的正常工作有很大影響。它可作為安全閥、卸荷閥和加載閥等使用，也可與遠程調壓閥組合以實現遠距離調壓等。圖1中，先導型溢流閥在液壓回路中用作安全閥，防止液壓系統過載。正常工作情況下，系統壓力不超過溢流閥的調定壓力時，溢流閥關閉不起溢流作用。當系統壓力達到溢流閥的調定壓力值時，溢流閥打開，將油液溢回油箱，使壓力不再上升，以保證系統的安全。文中進行的實驗人為設置了在主閥芯的阻尼孔處穿上一根細導線的故障。

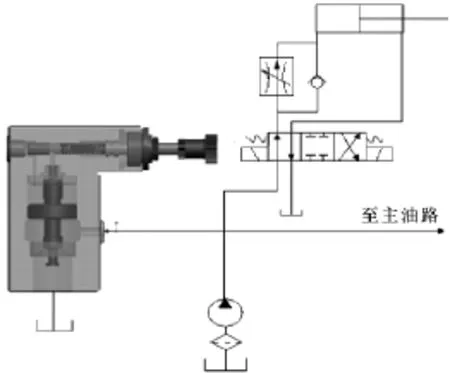
圖1 溢流閥工作回路

實驗分別在溢流閥正常工作狀態和故障狀態各自采集了10組和11組共21組數據。實驗使用的數據個數為512個。

4 譜圖

為了進行故障識別，將實驗中測得的正常狀態和故障狀態的21組數據分別求出其雙譜對角切片和倒雙譜。在正常狀態和故障狀態下，在3種不同的油壓下 (1 MPa、2 MPa、4 MPa)，將兩種狀態的雙譜對角切片和倒雙譜各選取1組示于圖2—5。其中圖2、3的x軸表示頻率，單位為Hz，y軸表示歸一化后的幅值大小，無量綱。由圖4、5的x軸表示數據，單位為個，y軸與圖2、3相同，也表示歸一化后的幅值大小，無量綱。可以看出，在倒譜方式下，從圖像峰值的構成和數量來看，2種狀態的區分較為明顯。

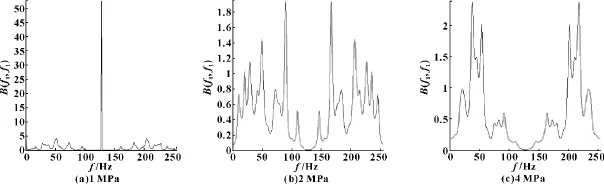
圖2 正常狀態雙譜對角切片圖

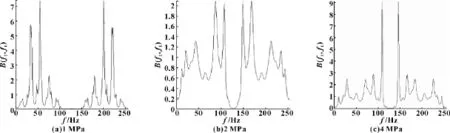
圖3 故障狀態雙譜對角切片圖

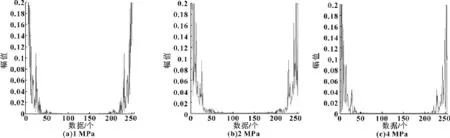
圖4 正常狀態倒雙譜圖

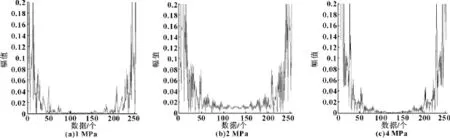
圖5 故障狀態倒雙譜圖

5 實驗結果與分析

為了有效判別故障，分別利用雙譜對角切片和倒雙譜作為工具，鑒于雙譜對角切片的光滑性和倒雙譜的時序性，分別計算了信號在正常狀態和故障狀態下雙譜對角切片的容量維以及倒雙譜的關聯維。正常狀態以及故障狀態倒雙譜的關聯維數值示于表1。為了在直觀上有效區分故障診斷結果，通過EXCEL軟件繪制了倒雙譜關聯維數值的點折線圖，見圖6。圖6的橫坐標代表數據，單位為組，縱坐標表示計算出的關聯維數值，無量綱。從圖6中可以看出，在倒譜方式下，正常狀態和故障狀態下信號的關聯維數在整體上區別較為明顯，為了準確統計診斷正確率，特選定故障狀態第1組數據的關聯維數值作為分界值，即以關聯維數值大于等于0.456 2確定為故障狀態，以小于0.456 2確定為正常狀態，則正常狀態和故障狀態誤判的數據個數分別是2個和1個，總體正確率為3/21＝1/7，超過了85%，這一結果在故障診斷中算是良好的。文中同時對相同信號的雙譜對角切片的容量維進行了計算，結果如圖7。圖7的橫坐標代表數據，單位為組，縱坐標表示計算出的容量維數值，無量綱。從圖中可以看出，兩種狀態難以區分。為了進行對比，還對信號的倒譜計算了關聯維以及信號的功率譜計算了容量維，信號的倒譜和功率譜分別在正常狀態和故障狀態下選取一組，如圖8—11所示。圖8、9的坐標意義與圖4、5相同，圖10、11的坐標意義則與圖2、3相同。倒譜關聯維和功率譜容量維的計算結果見圖12和圖13，圖12和圖13的坐標意義分別與圖6、7相同。圖12和圖13所表示的2種狀態均難以區分。

表1 正常狀態和故障狀態倒雙譜的關聯維數值

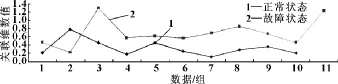
圖6 正常狀態和故障狀態倒雙譜關聯維折線圖

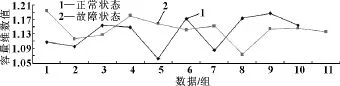
圖7 正常狀態和故障狀態雙譜對角切片容量維折線圖

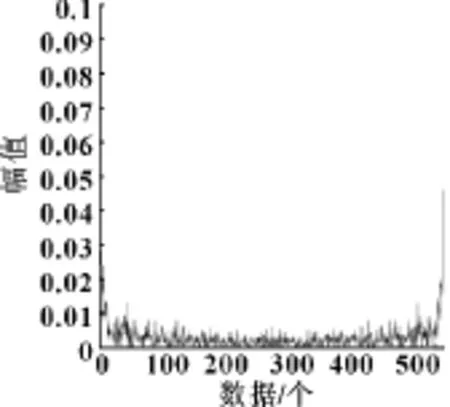
圖8 正常狀態倒譜

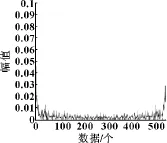
圖9 故障狀態倒譜

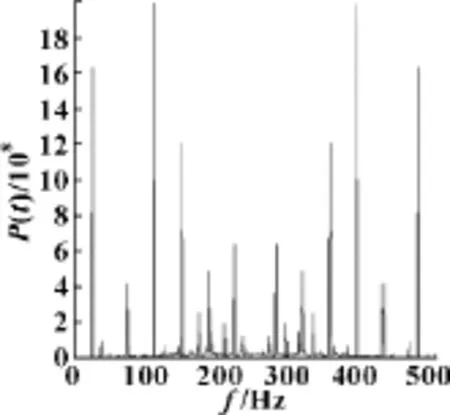
圖10 正常狀態功率譜

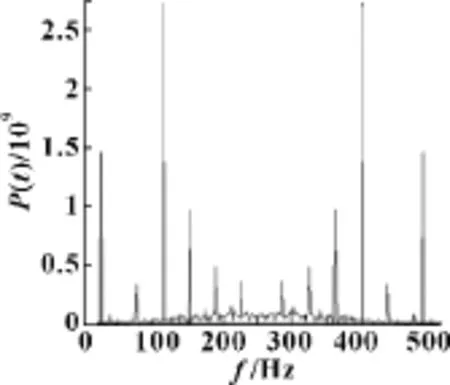
圖11 故障狀態功率譜

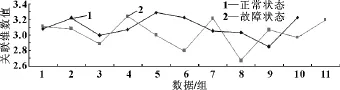
圖12 正常狀態和故障狀態倒譜關聯維折線圖

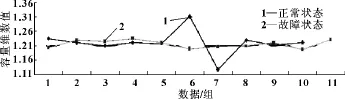
圖13 正常狀態和故障狀態功率譜容量維折線圖

文中在所選用實驗數據的基礎上，通過對比功率譜、倒譜、雙譜對角切片以及倒雙譜的故障診斷效果，得出了倒雙譜能取得最佳診斷效果的結果。由于雙譜可以從采集信號中最大限度地剔除掉噪聲的干擾，從而有效提取信號中的信息。這說明雙譜具有很強的消噪能力，理論上可以抑制高斯噪聲。對信號進行分析得出它的倒譜參數的過程稱為同態處理，倒譜參數所包含的信息也比其他參數多，同時受信號傳遞路徑的影響較小，但噪聲對倒譜分析的結果具有較大的影響。倒雙譜則將兩者的優點很好地結合了起來。由于分形維數能在直觀上度量不規則圖形的粗糙度，因而振動信號倒雙譜的分形維數可以在一定程度上反映機械設備在不同運行期間運行性質的變化，可以直接反映該設備在此期間的運行狀況。因此，文中的實驗數據在通過功率譜、倒譜以及雙譜對角切片都未能取得理想效果時，通過計算倒雙譜的分形維數而取得了良好的故障診斷效果是完全可以從理論上得到合理解釋的。

6 結論

通過計算倒雙譜的分形維數而取得了良好的故障診斷效果，說明在現有理論的基礎上，通過將各種方法的優點相結合的方式來提高機械故障診斷正確率的方式是可行的。

［1］KOCUR Dusan，STANKO Radoslav.Order Bispectrum:A New Tool for Reciprocated Machine Condition Monitoring［J］.Mechanical Systems and Signal Processing，2000，14(6):87l-890.

［2］蔣雨燕，黃宜堅.時間序列雙譜在調速閥故障診斷中的應用［J］.集美大學學報，2008，13(2):175-179.

［3］李輝，鄭海起，唐力偉.基于倒階次譜分析的齒輪故障診斷研究［J］.振動與沖擊，2006，25(5):65-68.

［4］李輝，鄭海起，唐力偉.基于倒雙譜分析的軸承故障診斷研究［J］.振動、測試與診斷，2010，30(4):353-356.

［5］吳文兵，黃宜堅，陳文薌.基于機械故障診斷的高階譜耦合性能分析［J］.振動、測試與診斷，2012，32(1):130-134.

［6］王春來，吳愛祥，劉曉輝.深井開采微震活動容量維Df變化特征［J］.北京科技大學學報，2010，32(11):1379-1382.

［7］張燕平，黃樹紅，高偉.關聯維數在汽輪機故障診斷中的應用［J］.華中科技大學學報:自然科學版，2007，35(7):93-95.