基于AMESim的直驅式電液伺服舵機控制系統的建模與仿真

王俊鋒，游有鵬

(南京航空航天大學機電學院，江蘇南京210016)

0 前言

電液伺服舵機是一個高精度的位置伺服控制系統，它在飛行器的姿態和軌跡精度控制起著決定性作用。直驅式電液伺服舵機是伺服電動機技術與液壓技術的結合，它通過伺服電機直接驅動滾珠絲杠帶動液壓缸活塞運動方式代替了結構復雜的電液伺服閥和易出現故障的變量泵，并由高壓油液直接驅動擺動馬達帶動負載轉動。控制簡單、高效、節能、集成化、價格便宜。

但是直驅式電液伺服舵機系統也存在一些不足，如轉動慣量很大、外負載復雜多變、易受系統泄漏和油液彈性模量系數的影響，且存在一定的時滯，影響了舵機系統的動靜態特性，是一種時變特性顯著并具有非線性特性的電液伺服系統。對于這樣的系統，普通的PID控制策略并不適合，而單一神經元網絡自適應PID是神經網絡與PID的結合，它不僅繼承了神經網絡大規模并行處理，高度的容錯性和魯棒性、自組織學習和實時處理等特點，而且兼有普通PID簡單、實用易于調節的特點，它能夠有效地優化PID參數，克服傳統PID的不足，實現對非線性、時變系統智能控制。

我國的直驅式電液伺服舵機研究起步比較晚，其設計和制造水平與發達國家有很大差距，隨著航空航天技術的飛速發展。飛行器的控制精度也越來越高，也對直驅式電液伺服舵機的性能提出了更高的要求。AMESim作為一種液壓系統專用仿真軟件，可采用基本元素法按照實際物理系統來構建仿真模型，能夠方便地對多學科跨專業復雜系統進行不同領域的模塊進行建模與仿真分析。本文作者利用AMESim仿真平臺建立了某直驅式電液伺服舵機控制系統的仿真模型，對其性能進行了分析，結果表明該方法有效可行。

1 直驅式電液伺服舵機工作原理

文中設計的直驅式電液伺服舵機以伺服電動機驅動滾珠絲杠，滾珠絲杠的滑塊與液壓缸的活塞桿相連，通過改變伺服電機的轉速和工作時間來改變液壓缸油液輸出量 (電動伺服泵)，最終控制擺動馬達的輸出，其最大的特點是發揮伺服電機的特性，避免了傳統電液伺服中電磁閥泄漏和變量泵故障多的缺點，無溢流損失、節流損失、體積小、效率高，操作控制簡單方便。該系統的工作原理如圖1所示，飛控計算機給出的舵面偏角指令信號，電位計根據舵面偏轉角度實時產生反饋信號，控制器將兩者進行比較，輸出操縱指令驅動電機偏轉，電機經減速器帶動滾珠絲杠旋轉，絲杠螺母與液壓缸活塞桿相連作往復直線運動，推動液壓缸工作腔高壓油液流入擺動馬達，推動馬達旋轉，馬達轉子與舵機轉軸一體安裝，帶動舵面產生偏轉，從而改變飛行器航行姿態或航行軌跡以達到控制器飛行軌跡的目的。圖中溢流閥起安全保護作用，防止過載損壞系統部件;蓄壓器用于低壓腔補油。

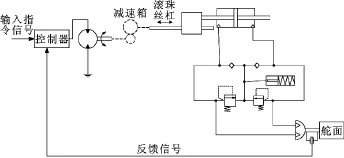
圖1 直驅式電液伺服舵機系統工作原理

2 系統建模

2.1 直驅式電液伺服舵機控制系統建模

直驅式電液伺服舵機控制系統由伺服電機驅動、減速器、滾珠絲杠，雙出桿液壓缸、擺動馬達、電位計等組成。為分析系統運動規律，列出伺服電機—減速器—滾珠絲杠—伺服液壓缸—擺動馬達的動力運動學方程如下:

(1)由伺服電機與減速箱之間運動關系可得:

整理得電機軸力矩平衡方程:

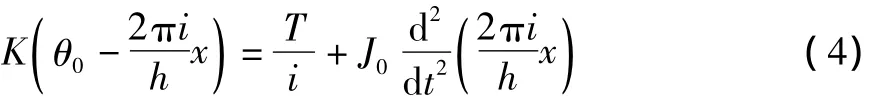
式中:J0為電機軸轉動慣量;T為滾珠絲杠上的力矩;θ為電機轉角;k為滾珠絲杠扭轉剛度;M為電機驅動力矩;h為滾珠絲杠的導程;θ0為電機軸輸入轉角;x為滑塊位移量;i為減速箱減速比。

(2)由電機軸與滾珠絲杠力矩平衡得到滾珠絲杠的運動力矩平衡方程:

其中:J1為滾珠絲杠的轉動慣量;θ為滾珠絲杠的轉角;M為滾珠絲杠運動的阻力矩;F為活塞連桿的驅動力;m為絲杠滑塊及連桿活塞質量;μ為阻尼系數。

整理得:

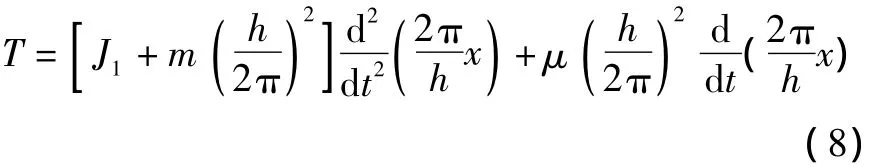
(3)假設油溫和體積彈性模量為常量，伺服液壓缸流量方程為:

式中:A為伺服液壓缸活塞有效面積;q為伺服缸推油量。

(4)根據流量和擺動馬達的排量可得擺動馬達輸出轉角方程:

式中:b為擺動馬達的葉片厚度;D為擺動馬達外殼內半徑;d為擺動馬達轉軸半徑。

對式 (4)、(8)、(9)、(10)分別進行拉普拉斯變換，消除中間項可得馬達輸出轉角與電機輸入轉角的傳遞函數:

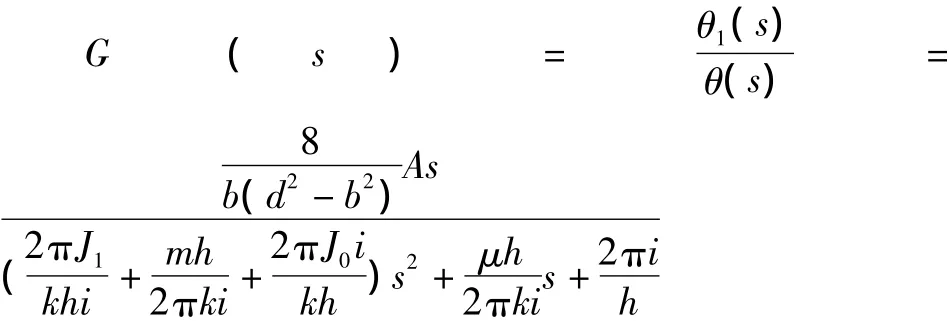
2.2 單一神經元自適應PID建模

為改進舵機的伺服性能，將單一神經元自適應PID引入舵機控制系統，它把神經網絡技術和常規PID控制器相結合，利用神經網絡的自學習功能和非線性函數的表示能力，遵從一定的最優指標，在線智能地調整PID控制器的參數，使之適應被控對象參數以及結構的變化和輸入參考信號的變化，并抵御外來擾動的影響。

神經元PID自適應控制方法的原理如圖2所示。

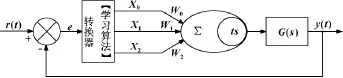
圖2 神經元PID自適應控制方法原理

如圖2所示，系統通過學習算法將誤差轉換為神經元，通過神經元權值wj的自適應調整使被控對象的輸出信號y(t)跟蹤r(t)的變化。

令神經元的輸人變量為:

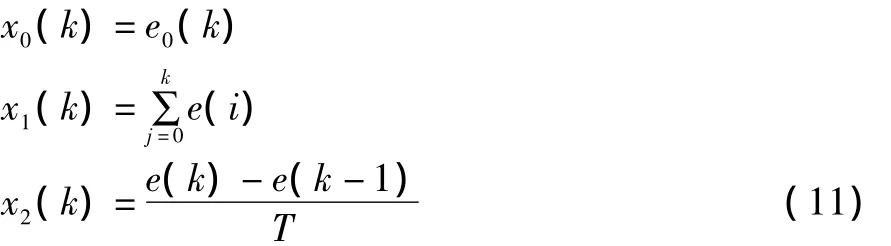
則神經元輸出為:

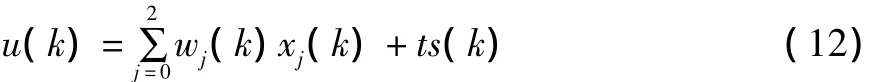
其中:wj為神經元權值;ts為神經元閾值;k為迭代次數。

采用Delta算法調節wj，則調節公式為:

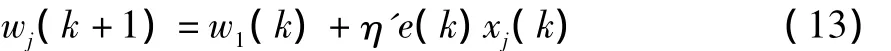
其中η'為學習率，神經元閾值調節公式為:

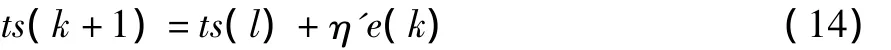
上面兩式兩端同除以輸入信號的采樣周期T，可得

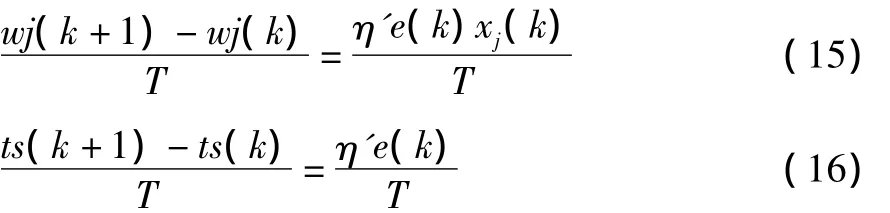
合并神經元的學習率和采樣周期，令η'/T＝η，若T取得足夠小，可把離散變量看成連續變量，離散變量k用連續時間變量t代替，則有:

對上面兩式分別積分得:

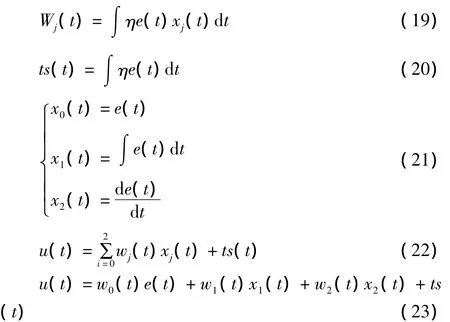
由此可見U(t)可分成比例環節、積分環節、微分環節和閾值4個部分，如圖3—6所示。

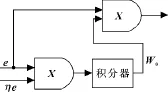
圖3 比例環節

圖4 積分環節

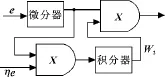
圖5 微分環節

圖6 閾值

基于AMESim軟件平臺，可構建如下單一神經元自適應PID模型。

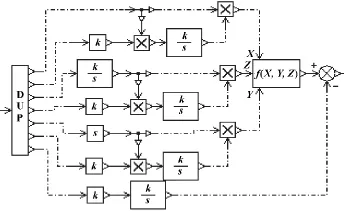
圖7 單一神經元自適應PID模型

為了簡化結構，將復雜單一神經元自適應PID模型生成超級模塊。

2.3 仿真平臺搭建

直驅式電液伺服舵機控制系統主要由伺服電機、減速器、滾珠絲杠、雙出桿液壓缸、擺動馬達、電位計等組成。分析系統內各部分組成及原理，利用AMESim平臺建立相應仿真模型:

(1)在草圖模式下，按照系統的物理構成搭建如圖8所示的系統仿真模型。為了簡化結構，伺服控制部分控制器的仿真建模采用了單一神經元PID模型的超級模塊。

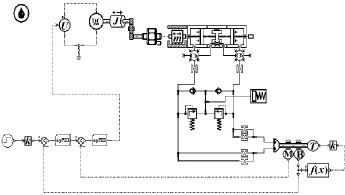
圖8 基于AMESim的直驅式電液伺服舵機控制系統仿真模型

(2)在給元件分配子模型時，為了便于初步分析，使用首選子模型功能為每個元件分配最簡單的子模型。

(3)在參數模式下為各元件設定具體參數。主要參數設置:電機最大轉速12 000 r/min，減速器減速比1∶4，滾珠絲杠導程2 mm，活塞最大位移50 mm，擺動馬達最大角行程 60°，擺動馬達排量24.115 2 mL/r，安全閥開啟壓力27 MPa，負載為140sinθN·m(θ為舵面與飛行器機體的夾角，140 N·m為假定舵面與飛行垂直時對軸的扭矩)，其他參數為默認值。

3 仿真結果分析

為了對比分析，分別采用普通PID和單一神經元自適應PID進行控制，在AMESim環境下建立仿真模型，給系統施加不同的輸入信號，得到直驅式電液伺服舵機控制系統的響應曲線。

圖9是直驅式電液伺服舵機控制系統對階躍信號響應的仿真曲線。圖 (a)是幅值為15°時的響應曲線，圖 (b)是幅值為30°的響應曲線。

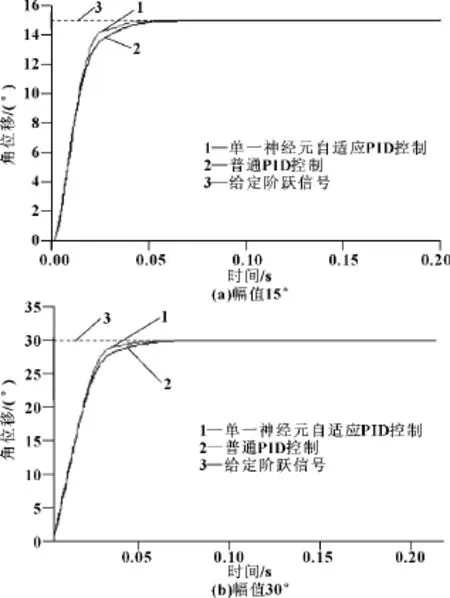
圖9 直驅式電液伺服舵機控制系統階躍信號響應曲線

圖10 為直驅式電液伺服舵機控制系統對正弦信號響應的仿真曲線。圖 (a)是頻率為1 Hz，幅值為30°的響應曲線，圖 (b)是頻率為5 Hz，幅值為30°時的響應曲線。

由圖 (a)可知，單一神經元自適應PID控制經過0.052″到達并穩定于幅值15°;普通PID控制經過0.067″到達并穩定于幅值15°。由圖 (b)可知，單一神經元自適應PID控制經過0.07″到達并穩定于幅值30°;普通PID控制經過0.089″到達并穩定于幅值30°。由此可見單一神經元自適應PID控制比普通PID控制響應快。

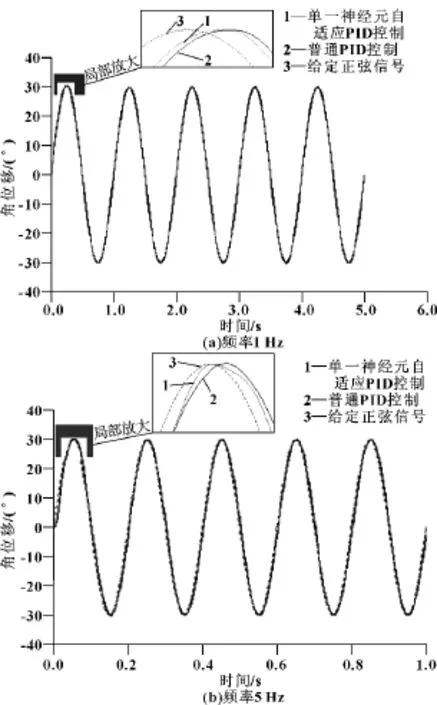
圖10 直驅式電液伺服舵機正弦信號響應曲線 (幅值30°)

由圖10所示可知，在輸入正弦信號時，單一神經元PID控制和普通PID控制舵機系統響應曲線相差不大，相位滯后較小，且幅值無明顯衰減，可見系統能夠用于高響應場合，適應飛行器快速響應要求。

對以上的仿真結果分析可知:直驅式電液伺服舵機在舵面轉動角速度及角度位置控制過程中，采用單一神經元自適應PID控制策略是可以滿足高響應控制要求的，且性能優于普通PID控制，系統響應快、位置誤差較小、無超調現象。仿真結果說明該直驅式電液伺服舵機控制系統能夠滿足飛行器快速定位場合的要求。

4 結論

(1)根據仿真結果可知，采用單一神經元自適應PID進行控制，不僅能夠提高系統響應速度，同時也能夠避免系統產生超調，保證了系統的快速性和準確性。

(2)上述結果表明該直驅式電液伺服舵機的控制系統在外加變負載情況下正反向運動，均能夠快速響應，且無超調量，滿足系統設計要求，這與電液系統響應速度快、位置誤差小、控制精度高的特點是相符合的。

［1］張新華，楊瑞峰.電動伺服系統剛度測試方法的AMES-im仿真［J］.振動、測試與診斷，2013(5):195-197.

［2］王群，吳寧，王兆安.神經元PID自適應控制方法的模擬電路實現［J］.電氣傳動，1998(4):24-27.

［3］付永領，祁曉野.AMESim系統建模和仿真:從入門到精通［M］.北京:北京航空航天大學出版社，2006.

［4］萬保中，常虹，姜繼海，等.直驅式電液伺服油動機的建模與仿真研究［J］.液壓氣動與密封，2013(11):20-24.

［5］傅曉云，黎飛，李寶仁.某水下航行器舵機液壓伺服系統建模仿真［J］.機床與液壓，2010(7):151-153.

［6］唐凱，廖瑛，何星星，等.液壓舵機一體化建模與聯合仿真方法研究［J］.彈箭與制導學報，2011，31(3):207-210.

［7］陳士龍，王彬.渦輪流量計校準裝置仿真研究［J］.計算機仿真，2014(4):56-59.

［8］謝國慶，周曉明，金梁斌.基于AMESim的電液位置控制系統動態性能仿真分析及優化［J］.機床與液壓，2014(2):47-49.