用余震序列估算震源地殼的黏度

李成波，李建新

（安陽工學院數(shù)理學院，河南安陽455000)

0 引言

巖石變形的脆—塑性轉(zhuǎn)換涉及巖石圈強度、地震發(fā)生的條件和地震機制等問題，而巖石的黏彈性質(zhì)是地球動力學的重要參數(shù)之一。一定溫度和壓力條件下的地殼物質(zhì)，在外力長時間作用下具有流變性。因此，研究地殼物質(zhì)的運動狀態(tài)時，必須考慮黏滯性。此外，在研究地震波傳播時，也要考慮黏滯性及能量損耗的影響。張國民[1]等分析了地殼介質(zhì)的流變特征，進而探討了震源深度分布的物理解釋和孕震環(huán)境。Zang[2]等考慮了摩擦滑動、脆性破裂及蠕變等三種主要的流變機制作用，計算了華北巖石圈的三維黏度分布。

通常，在對巖石介質(zhì)的流變特性進行計算模擬過程中，主要用到兩類流變模型，黏彈性模型和彈塑性模型。兩者的區(qū)別在于：彈塑性模型，只有在外加應力大于內(nèi)部屈服應力時，巖石介質(zhì)才會發(fā)生流變現(xiàn)象；而對于黏彈性模型，不管外加應力是多少，都會產(chǎn)生流變現(xiàn)象。這些模型都可以近似模擬巖石介質(zhì)的流變特性，哪個模型最好？為了解決這一選擇問題，首先進行各類巖石的蠕變實驗，得到了對應的蠕變曲線，再用各種常用模型去擬合實驗數(shù)據(jù)。對比常見的Kelvin和Maxwell黏彈性模型，前者的特點是沒有考慮到黏彈性體的瞬時響應，后者的特點是在外加應力卸載以后介質(zhì)不能恢復原狀，而標準線性固體模型（廣義開爾文體力學模型）就能較全面地反映巖石介質(zhì)的流變特征，不僅能產(chǎn)生瞬時的彈性應變，也可以產(chǎn)生隨時間變化的蠕變效應。

本文由實驗數(shù)據(jù)得到標準線性固體模型的元件模量μ2與巖石介質(zhì)模量之間的定量關(guān)系之后，再來處理南黃海和溧陽地震[3]后的余震序列，得到累計能量釋放或應變釋放與時間的關(guān)系曲線，結(jié)合μ2＝25μ的實驗結(jié)果來估算該地區(qū)的巖石介質(zhì)黏度。

1 蠕變實驗

實驗用的巖石采自郯廬斷裂帶附近，加工成大小為50 mm×50 mm×50 mm的樣品。實驗裝置為全自動伺服液壓試驗機(YAW4605)系統(tǒng)，加有水冷設(shè)施，可保證壓機系統(tǒng)連續(xù)穩(wěn)定工作兩個月。在樣品表面對稱貼有兩組電阻應變片，與數(shù)字式應變儀（WS-3811）連接，采樣頻率為1Hz。用鋼塊對實驗裝置進行了穩(wěn)定性測試，應力和應變測量值是二條基本平行的直線，分別有±0.2MPa和±3微應變的波動。每次實驗開始時，首先對樣品迅速加壓，讓應力在幾分鐘內(nèi)到達設(shè)定值，然后保持，應力可看成是階躍函數(shù)。在整個實驗過程中，保持室溫基本不變，分別在不同的恒定應力下進行蠕變實驗。

典型的巖石實驗蠕變曲線如圖1所示。開始時，應力很快上升到70MPa，應變也隨之上升到1468微應變。然后應力保持不變，而應變繼續(xù)緩慢上升。用不同的模型對實驗數(shù)據(jù)進行擬合，最后認為用標準線性固體模型（廣義開爾文體力學模型）來表示巖石的這種黏彈性較好[4]。圖2所示為標準線性固體的兩種等價模型，圖中E1代表彈性元件的彈性系數(shù)，產(chǎn)生瞬時彈性應變。E2和η分別代表并聯(lián)彈性元件的彈性系數(shù)和黏性元件（阻尼盤）的黏性系數(shù)，產(chǎn)生隨時間變化的蠕變變形，該模型的本構(gòu)方程為[5]

式中ε為軸向應變，σ0為軸向應力，τ＝η/E2為弛豫時間，t為實驗持續(xù)時間。從圖1中可以看出式（1）能夠很好地模擬巖石在恒定應力作用下的蠕變特性，實測曲線和反演曲線的相關(guān)系數(shù)可達到0.99。

根據(jù)實驗所得蠕變曲線和已知的恒定應力σ，通過擬合求得E1、E2和τ等模型參數(shù)的數(shù)值。如果在沒有蠕變實驗結(jié)果做參考的情況下，采用E＝E1＝E2的簡化條件，來計算巖石介質(zhì)的黏度，就會產(chǎn)生很大的誤差。根據(jù)大量不同類巖石的蠕變實驗結(jié)果，能總結(jié)出μ2＝E2=25μ的實驗規(guī)律，用公式來估算巖石介質(zhì)的黏度更為合理。

2 南黃海和溧陽地震余震序列的處理

由于地殼巖石的非完全彈性，一般來說一次主震不太可能將所蓄積的能量一次性釋放完，剩余的部分能量將在彈性恢復、調(diào)整平衡的過程中以余震形式陸續(xù)釋放出來。圖3為張國民等提出的孕震模型，其中a圖為力學抽象模型，由兩個臂并聯(lián)，其中一個臂為彈簧和滑塊的串聯(lián)，另一臂為麥克斯韋爾體，模擬地殼的塑性流動變形。當發(fā)生地震即t0時，滑塊滑動產(chǎn)生一個應力降，隨后進入余震期t0～t1，應力逐漸減小。我們所處理余震序列就是在這之后相對短暫的時期，這個時候的力學模型可以用標準線性固體（圖1）代替，即彈簧和開爾文體的串聯(lián)，下文中對余震序列的處理都將用到此模型。

在一次地震后不久的時間內(nèi)，在同一地震斷裂帶上發(fā)生的余震，認為是應力解除后，將主震未完全釋放的能量繼續(xù)釋放出來的過程。蠕變實驗是黏彈介質(zhì)的加載過程，主震余震序列則可看成黏彈介質(zhì)的卸載過程。

1979年7月9日在溧陽發(fā)生了6.3級地震，主震深度為12km，余震深度范圍大部分在10～14km。1984年5月21日在南黃海發(fā)生了5.7級和6.2級的雙震型地震，兩個主震間隔70s。兩次地震的主要參數(shù)見表1所示。

表1 各個地震主要參數(shù)

對于每次地震的數(shù)據(jù)做如下處理：把釋放的能量轉(zhuǎn)換成應變，累積的能量轉(zhuǎn)換成累計的應變。能量開平方后看成應變，單位以J1/2表示，以月為單位統(tǒng)計余震能量，時間軸以天表示。如圖4和圖5所示，圖中小圓圈代表所取的數(shù)據(jù)離散點，對比圖1和圖4、圖5可看出，每次主震后余震釋放能量的過程與巖石蠕變實驗中的應變累積過程非常相似，可以認為釋放是積累的逆過程，說明地殼的巖石介質(zhì)雖然以彈性為主，但也不能忽略其蠕變效應。用式（1）對數(shù)據(jù)進行擬合計算，分別可以得到對應的弛豫時間τ，地殼巖石的模量μ取4.0×1010Pa，代入公式（2）進行計算，即可得到該震源區(qū)地殼巖石的黏度系數(shù)η，結(jié)果見表2。

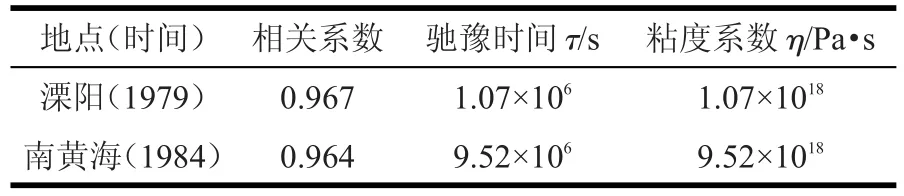
表2 擬合過程的部分結(jié)果

利用標準線性固體模型，通過對江蘇溧陽和南黃海兩次地震的余震序列資料的處理，計算得出兩地震源區(qū)地殼的黏度在數(shù)量級上是一致的。對余震序列資料的處理可以根據(jù)序列資料數(shù)量和時間的不同按照不同的時間段進行統(tǒng)計，如直接使用原始序列資料，可以按旬或按月進行統(tǒng)計等（本文按月統(tǒng)計），在模型反演圖形會有一定的差別，但計算的結(jié)果都是在同一個數(shù)量級。

3 結(jié)論和討論

根據(jù)巖石蠕變實驗的結(jié)果，用標準線性固體模型來擬合實驗數(shù)據(jù)相關(guān)系數(shù)很高，也比較符合巖石的非彈性特征。把溧陽和南黃海兩次地震后余震釋放的能量轉(zhuǎn)換成應變，并按月累計，得到和蠕變實驗非常相似的變形曲線，結(jié)合孕震模型，如采用標準線性固體擬合數(shù)據(jù)較為合理。經(jīng)計算求出模型的弛豫時間，并得到該震源區(qū)地殼巖石的黏度系數(shù)在1018Pa·s數(shù)量級。考慮到地殼巖石圈黏度的分層和地區(qū)差異，而文中所用到的地震震源深度又相對比較淺，綜合來看，得到的黏度系數(shù)數(shù)量級和有關(guān)文獻還是相一致的。

另外，計算所用的余震序列資料除了應該滿足數(shù)量上（即余震能量釋放）的要求外，還應該滿足時間上的要求。若余震發(fā)生時間（或能量釋放時間）過短，盡管余震數(shù)量足夠多，但也會影響到計算結(jié)果的精度，最大可能造成一個數(shù)量級上的差別。所以并不是所有的主震余震序列都可以用來反演震源地殼的黏度，如何克服余震序列在時間和數(shù)量上的限制還需要進一步深入研究。

[1]張國民，李麗.地球介質(zhì)的流變性與孕震模型[J].地震地質(zhì)，2003，25(1):1-10.

[2]ZANG Shao-xian,LI Chang,NING Jie-yuan,et al.A preliminary model for 3-D rheological structure of the lithosphere in North China[J].Science in China(Series D),2003,46(5):461-473.

[3]尹祥礎(chǔ).固體力學[M].北京:地震出版社，1985.

[4]SHI Xing-jue,WEN Dan,BAO Xue-yang,et al.Application of rock creep experiment in calculating the viscoelastic parameters of earth medium[J].Science in China(Series D),2006,49(5),492-498.

[5]田建明，徐徐，謝華章，等.江蘇及南黃海地區(qū)歷史地震類型分布特征[J].地震學報，2004，26(4)：432-439.