團隊生產最優激勵研究

西南財經大學財政稅務學院 鄭棱杰 北京大學軟件與微電子學院 隆正偉

一、引言

隨著經濟的快速發展，團隊分工愈加專業化，任何人都不可能獨立完成所有的工作，企業產品的生產需要各成員發揚群策群力，相互合作的團隊精神。因此，團隊生產的重要性愈來愈受到企業的重視。在很多情況下，生產產出需要的是團隊成員之間的合作，但由于在團隊中委托人和代理人之間的信息不對稱，難以觀測和計量到團隊的每個成員對于總產出的具體貢獻。因此，企業在多數情況下只能根據團隊的總產出來對每個成員進行激勵。本文假設企業對于團隊成員的激勵是通過團隊的總產出進行的，且只能為底薪加抽成這一線性激勵機制，分析在團隊成員的努力之間存在和不存在互補性的兩種情況下，企業對于團隊成員的最優線性激勵機制。發現前一種情況，即當團隊成員的努力之間存在互補性時，企業對于團隊成員的最優線性激勵系數應大于后一種情況下企業對于團隊成員的最優線性激勵系數。

二、文獻綜述

國內外已有學者對團隊生產的激勵機制作了廣泛的研究。Holmstrom（1982）指出成員間的合作導致了搭便車問題，并指出打破預算平衡是解決搭便車問題的關鍵，這為研究團隊生產激勵問題提供了切入點。在研究企業生產函數方面，Bernd Irlenbuscha（2008）認為團隊成員的生產函數應該包含一個不確定因子，因為在實際中由于有天災等不確定因素存在，團隊的總產出并不僅僅與團隊成員努力程度呈正相關關系，即假設團隊成員是風險規避型的。葉紅心等（2002）在解決團隊生產中，追求利益最大化的個體理性與集體理性之間的矛盾問題時，則認為團隊成員的收益與自身的努力程度呈正比，即假設團隊成員是風險中性型的。

本文在研究中，假設團隊成員為風險中性型的，即生產函數中不包含不確定因子。而在企業給予團隊成員的最優線性激勵系數上，由于Adams（2008）的生產函數是建立在CES生產函數上的，其假設團隊每一個成員的彈性系數是一樣的。因此認為企業對于團隊每個成員的最優線性激勵系數應該相等。而本文所建立的生產函數由于團隊成員的彈性系數互不相同，因此，推導出來的企業對于團隊兩成員的最優線性激勵系數并不是一致的。另一方面，Adams認為影響企業總產出的因素除了團隊成員的努力程度外，還有加入企業對于團隊成員監督所引起企業產出額外的增加量。在這一點上，本文簡化了企業的總產出，認為其是由團隊成員的努力程度所決定的，而企業則不存在對團隊成員的監督。

在團隊生產的博弈中，黃國華等（2009）構建由兩成員組成的團隊生產模型，在生產函數假設為柯布—道格拉斯形式時，研究兩成員的收益最大化時各自的努力程度。同樣，Heywood（2012）則考慮了企業生產函數為線性式生產函數時，當線性式生產函數呈現規模報酬遞減，不變，遞增三種情形時，團隊兩成員為達到收益最大化所應采取的最優努力程度。但由于他們涉及的是兩個成員為追求收益最大化時的博弈。意味著團隊兩成員對于總產出具有完全的支配權。因此，他們并沒有研究相當于團隊領導人的第三方存在的時候，對于團隊兩成員的激勵問題。而本文則是在分別構建柯布—道格拉斯與線性式生產函數的基礎上，討論了當存在團隊領導者——企業的時候，其和團隊兩成員為追求各自收益最大化時的博弈。探討企業對于團隊兩成員的最優線性激勵問題。同時，本文分別探究在柯布—道格拉斯與線性式生產函數下，企業所應給予團隊成員的最優線性激勵系數的大小關系。由于企業不同的生產函數意味著團隊成員的努力程度之間存在的互補性的有無，而互補性的有無會對企業關于團隊成員的最優線性激勵系數產生影響。因此，筆者認為有必要建立企業和團隊成員的博弈模型，通過對兩個成員努力之間互補性的有無分析，確定在這兩種不同的情況下企業最優線性激勵系數的大小關系，并為現實中存在互補性的企業，對于團隊成員的線性激勵系數較高這一事實提供一定的理論基礎。

三、模型構建

（一）模型引入 通常一個團隊是由多人組成的，但是為了分析，將問題簡化為如下模型,在一個企業內，有企業、成員A、成員B三個參與者。用a表示成員A努力的生產彈性系數，代表成員A的產出比重，用b表示成員B努力的生產彈性系數，代表成員B的產出比重；且滿足a+b=1。而成員A和成員B對于工作的努力程度則由p1，p2分別表示。假設企業的總產出由團隊成員努力的生產彈性系數和努力程度共同決定。則有如下的生產函數：y=f（p1a，p2b）。

同時，用r1，r2分別表示企業給予成員A和成員B關于企業總產出的線性激勵系數。由于成員A與成員B的邊際成本隨著努力程度的提高而遞增，即成本函數的一階導和二階導皆大于0。這里為了簡化起見，假設成員A與成員B的成本函數為c，且c=x3。其中，x代表努力程度。這樣可以構造出成員A和成員B各自的收益函數：h1=r1f（p1a，p2b）-p13；h2=r2f（p1a，p2b）-p23。

企業給予團隊成員的線性激勵相當于成員A與成員B從企業總產出中拿到的抽成這一塊，由于企業給予成員A和成員B的底薪通常為常數，因此并不影響本文對于成員A和成員B最優努力程度的確定及對企業最優線性激勵系數的安排。這樣可以將企業的收益最大化簡化為團隊總產出減去給予成員A和成員B抽成后的剩余價值的最大化。相應的，企業的收益函數可以表示為：s=（1-r1-r2）f（p1a，p2b）。

上述生產函數表達式由團隊成員努力之間互補性的有無來決定。互補性表示團隊中一個成員努力程度的增加對另一個成員提高自身努力程度的動力。

互補性推導如下：

（1）柯布—道格拉斯式生產函數的表達式為：

對式（1）分別對求偏導，可求得成員A的邊際產出：

（2）線性式生產函數的表達式為：

同理，對式（3）分別求偏導，可求得成員A的邊際產出：

（3）對柯布—道格拉斯式生產函數互補性的分析：邊際產出表示的是增加一個單位可變要素投入量所增加的產出。

由推導可知，在式（2）中，當成員B的努力程度增加一個單位時，成員A的努力程度增加所帶來的總產量的增加量會大于式（4）中總產量的增加量。因為在線性式生產函數中，由式（4）可以看出，成員A的邊際產出和成員B努力程度的大小并無直接的聯系。因此，成員B努力程度的增加將不會對成員A的邊際產出造成影響。因為：（p2+1）b＞1，所以：a（p1+1）a-1（p2+1）b＞a（p1+1）a-1。這說明在柯布—道格拉斯生產函數下，由于成員B努力程度的增加，成員A努力程度的增加所帶來的總產出的增加量會更大。故在生產函數為柯布—道格拉斯的形式下，團隊兩個成員努力程度之間存在著互補性。

（二）兩種生產函數下的最優激勵機制

（1）模型的行動順序。

第一步：企業決定成員的工資是如何取決于團隊的總產出，即確定工資函數。表達式如下：

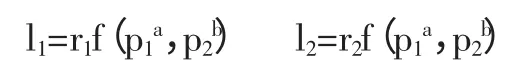
第二步：在觀察到工資如何取決于團隊總產出后，兩個成員同時決定自己的努力程度。

第三步：兩個成員付出努力并生產產出，成員根據團隊產出和第一步企業設定的工資函數得到自己相應的工資。

最優激勵機制的推導采用逆向歸納法。即先求解出企業設定的任意一個線性工資函數下，成員在第二步會選擇多高的努力程度。這個努力程度是企業設定的線性激勵系數的一個函數。然后逆推回第一步，企業在預期到設定的工資函數會如何影響工人努力的情況下，選擇一個工資函數來最大化自己的利潤。

（2）柯布—道格拉斯式生產函數。當生產函數滿足柯布—道格拉斯形式時，這時企業對應的生產函數為。此種情況下可以看出一個員工的努力提高了另一個員工努力的邊際產出，從而促使其更加努力。即團隊成員努力程度之間存在著互補性。

構造出成員A、成員B、企業具體的收益函數。

成員A的收益函數h1為：h1=r1cbp1ap2b-p13

成員B的收益函數h2為：h2=r2cbp1ap2b-p23

企業的收益函數s為：s=（1-r1cb-r2cb）p1ap2b

推導兩成員的最優努力程度以及企業的最優線性激勵系數。其中，成員A與成員B各自的收益函數如下：

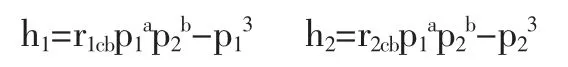
首先，討論兩成員之間的博弈關系。以成員A為例，由于成員A的工資函數是由企業所決定的，因此成員A會求得在任意一個線性工資函數下，能使自己的收益的得到最大化的努力程度。這個努力程度是成員B的努力程度和企業線性激勵系數的表達式。

其次，成員A知道成員B也會求出在任意一個線性工資函數下的使自己收益最大化的努力程度。同樣，成員B的努力程度是成員A的努力程度和企業線性激勵系數的表達式。這時，成員A可以聯立上述兩個表達式求出使自己收益最大的努力程度p1*。同理，成員B也可求出屬于自己的最優努力程度p2*。

則兩成員的最優努力程度分別為：

同時，企業也知道兩成員為實現自身收益最大化會采取最優的努力程度p1*與p2*。

這時，企業在預料到設定的工資函數會如何影響工人努力的情況下，選擇一個工資函數來最大化自己的利潤。即企業確定最優的線性激勵系數r1cb*、r2cb*來實現自身收益的最大化。

通過對企業的收益函數關于求偏導，企業可以求得最優的線性激勵系數r1cb，r2cb如下：

通過檢驗可知，此時的r1cb*，r2cb*正是可以使得企業收益取到最大值的線性激勵系數。

由于前面的假定，a+b=1，因此式（6）可化為：

事實上，在團隊生產中，企業在追求企業收益最大化時面臨一個決策。在柯布—道格拉斯生產函數下，由式（5）可知，當企業提高給予團隊兩成員的線性激勵系數時，這一線性激勵方式將會促使團隊成員們提高各自的努力程度，加之努力程度間互補性的存在，增大了企業總產出的增幅。而總產出的擴大對于企業來說相當于做大了收益這張餅，意味著企業能得到的收益更多了，但另一方面，企業給予團隊成員線性激勵系數的增加會最終減少企業得到這一張餅的比例。因此，企業需要從中作出一個權衡取舍。

因為企業給予團隊成員的最優線性激勵系數是在假設團隊兩成員皆采取最優努力程度時，使得企業收益最大化的決策。即最優線性激勵系數由最優努力程度，彈性系數所決定。但由于最優努力程度可由彈性系數進行間接表示。所以最優線性激勵系數其實是由團隊成員努力的生產彈性系數所決定的。

于是可得如下結論：

結論1：在規模報酬不變的柯布道格拉斯生產函數下，企業給予兩成員的最優線性激勵系數和兩成員努力的生產彈性系數成正比。即最優線性激勵系數和兩成員對于總產出的貢獻率成正比，當成員A與成員B任意一方的產出比重愈大時，其所獲得的抽成也就愈多。此結論1的正確性可以由式（7）得出。

在現實生活中，這種存在互補性的運行模式類似于銷售企業的運行管理模式。因為，在銷售企業中，員工為了完成銷售指標或是拿到更多的提成，他們便會就某項業務展開激烈的競爭，因為互補性的存在，使得一個員工的努力提高了另一個員工努力的邊際產出，因此往往某位員工優秀的業績會激發其它的員工奮起直追，這有助于企業總產出的增加。這些銷售企業對于員工們的線性激勵制度以底薪加提成為主。其中，提成占據薪酬的絕大部分。

（3）線性式生產函數。第二種生產函數滿足線性生產函數形式:即企業的生產函數表達式為y=p1a+p2a。此種情況可以看出兩成員的努力程度之間并不存在互補性，即一個成員努力程度的增加并不會提高另一個成員努力的邊際產出。以成員A為例，當成員A的努力程度增加一單位，成員B的努力程度的增加不會像第一種情況，使兩者的總產出有更大幅度的增加。

同樣，列出成員A、成員B、企業各自具體的收益函數：

成員A的收益函數h3為：h3=r1L（p1a+p2b）-p13

成員B的收益函數h4為：h4=r2L（p1a+p2b）-p23

企業的收益函數s為：s=（1-r1L-r2L）（p1a+p2b）

與第一種生產函數形式推導成員A與成員B的最優努力程度以及企業的最優線性激勵系數原理一致。先列出成員A與成員B各自的收益函數：

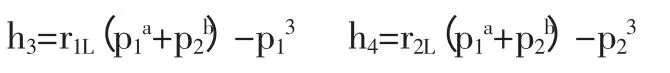
同樣，成員A和成員B在假定對方知道自己的最優努力程度并以此確定屬于對方的最優努力程度的情況下，分別對各自的努力程度進行求導，以求出能使得自身的收益取到最大值的努力程度。根據計算，可以得出成員A和成員B的最優努力程度:

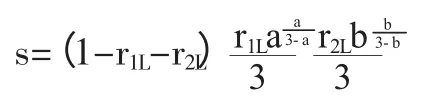
企業的目的亦是使其收益最大化，企業在假定成員A和成員B在追求自身收益最大化時，將會采取對自己最有利的努力程度。則此時企業的收益函數可表示為：

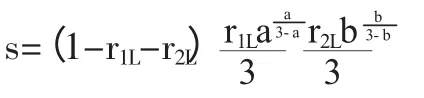
企業需要確定合適的線性激勵系數，使得自己的收益函數由此取到最大值，而這一合適的線性激勵系數便是最優線性激勵系數。

通過計算分析可知，最優線性激勵系數r1L*，r2L*無法用彈性系數a,b進行純粹的表示，即r1L*，r2L*不存在顯式解。因此，兩種形式生產函數的最優線性激勵系數的大小關系需要通過相關的分析與證明得出。

兩種形式生產函數的最優線性激勵系數分析。對當生產函數為柯布—道格拉斯形式與線性形式這兩種情況下的最優線性激勵系數的大小進行分析:

式（8）表示的是柯布—道格拉斯生產函數下團隊成員的最優努力程度。從式（8）中可以看出，當企業增加給予團隊兩成員的線性激勵系數時，團隊兩成員便會提高各自的努力程度從而增加了企業的總產出。一方面，企業將總產出做大了；另一方面，由式（9）企業的收益函數可以看出，因為企業對團隊成員線性激勵系數的提高使得企業最終得到這塊餅的比例減少了。

由于柯布—道格拉斯生產函數互補性的存在。使得當團隊成員努力程度的提高會帶來更大的總產出的增幅。因此，企業可以利用這個特性，通過給予成員A與成員B一個較高的線性激勵系數來做大總產出，從而獲得企業收益的最大化。

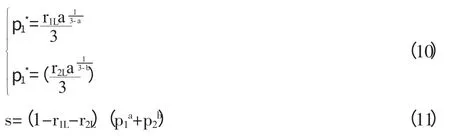
式（10）與式（11）為線性式生產函數下，團隊兩成員的最優努力程度與企業的收益函數。

同樣，當企業增加對于兩成員關于總產出的線性激勵系數時，團隊兩成員便會提高各自的努力程度，從而增加了企業總產出。但與柯布—道格拉斯生產函數情形下不同的是，由于線性式生產函數下，團隊成員努力程度間不存在互補性。因此，企業總產出的增幅較小。而企業可以利用這個特性，通過給予團隊兩成員較小的線性激勵系數來提高企業享有總產出這塊餅的比重，從而獲得企業收益的最大化。

于是可得以下結論：

結論2：在生產函數為柯布—道格拉斯形式時，企業給予團隊成員的最優線性激勵系數大于線性式生產函數下企業給予團隊成員的最優線性激勵系數。此結論2的正確性可通過嚴格的證明進行檢驗。

實際上，線性式生產函數形式適用于團隊成員努力程度間不存在互補性的企業，這類企業里的員工們通常以穩定的薪酬為主，其提成占總收入的比重小。且一個員工的努力程度提高并不會提高另一個員工努力的邊際產出，因此企業員工之間的競爭關系并不像銷售企業那樣的激烈。

由上面兩種生產函數的線性激勵系數大小比較可知：在企業的技術水平無法在短時間內提高的情況下，企業為了追求收益的最大化，在不存在互補性的企業里，企業給予兩成員的線性激勵系數應該小于存在互補性的企業中企業給予兩成員的線性激勵系數。

四、結論與建議

本文以企業不同的生產函數為切入點，討論在生產函數分別為柯布—道格拉斯形式與線性式形式時企業給予團隊成員關于企業總產出的最優線性激勵系數的大小關系。同時，將理論與實際結合，對兩種生產函數形式下最優線性激勵系數的大小關系進行合理的解釋。分析發現：（1）在規模報酬不變的柯布道格拉斯生產函數下，企業為實現收益最大化應賦予團隊成員較大的線性激勵系數。最優線性激勵系數的大小與團隊成員努力的生產彈性系數呈現正相關關系。（2）在不存在互補性的企業中，企業為實現收益最大化應賦予團隊成員較低的線性激勵系數。最優線性激勵系數的大小與團隊成員努力的生產彈性系數密切相關。（3）在團隊成員彈性系數之和為1的情況下，企業為了追求個人（企業）利益的最大化，在團隊成員努力程度間不存在互補性的企業里，企業給予成員A和成員B的線性激勵系數應該小于存在互補性的企業中企業給予兩成員的線性激勵系數。

針對上述結論，提出以下建議：（1）確定企業中成員的產出比重。根據經濟學中理性經濟人的假設，人總追求自身利益的最大化。因此，在企業和兩成員的三者博弈中，能夠確定自己的收益函數并采取策略實現自身收益最大化時十分有必要的。而兩成員的產出比重正是實現企業、成員A、成員B自身收益最大化的媒介。企業應根據兩成員的產出比重來確定其賦予成員A和成員B的線性激勵系數，同樣的，成員A和成員B應根據自身的產出比重來確定屬于自己的努力程度。因此，確定企業中兩成員的產出比重尤為重要。（2）在成員努力程度間不存在互補性的企業中，企業應完善評價指標和業績考核體系。由于線性式生產函數不存在互補性的特點，削弱團隊成員的工作積極性，成員們傾向于不努力，坐享其成。這種情況下企業應該完善相關評價指標的制定，如KPI管理模型，針對每一個成員進行激勵，同時引入業績考核體系，在這樣的考核體系下，團隊成員為了完成考核目標，會轉變工作態度從而提高自身的努力程度。（3）企業應判斷團隊成員努力程度間是否存在互補性來確定合適的抽成比重。由于在不存在互補性的企業中，推導出其最優的線性激勵系數r1L，r2L分別小于存在互補性的企業的最優線性激勵系數r1cb，r2cb，因此，企業在決定給予兩個成員的線性激勵系數時應考慮企業團隊成員努力程度間的互補性是否存在，如果是團隊成員努力程度間存在互補性的企業，企業應賦予兩個成員較大的線性激勵系數。反之，企業應賦予兩個成員一個較低的線性激勵系數。

［1］葉紅心、張朋柱：《團隊生產動態博弈》，《中國管理科學》2002年第10期。

［2］黃國華、周云：《團隊生產中的博弈模型與道德風險研究》，《數學的實踐與認識》2009年第6期。

［3］B.Holmstrom.Moral hazard in teams[J].Bell Journal of Economics,1982,13:324-340.

［4］Bernd Irlenbuscha，Gabriele K.Ruchalab.Relative rewards within team-based compensation[J].Labour Economics,2008,15(2):141—167.