面向換乘行為的城市公交客流分配及應用

曾 鸚 ，李 軍，朱 暉

（1.成都市社會科學院 經濟所，成都 610023；西南交通大學2a.經濟管理學院；2b.服務科學與創新四川省重點實驗室，成都 610031）

如何提高公共交通的客運能力與服務質量，以保持現有的公交用戶與吸引其他更多的出行者選擇公共交通已成為緩解城市交通擁堵最根本和最有效的措施，作為公共交通規劃的關鍵技術之一，同時也是交通需求分析和交通運營管理中最重要的一環，公交客流分配問題近年來已引起眾多學者的關注和重視[1-3]。

公交客流分配問題是指在公交網絡結構和有關參數（運輸能力、頻率和車頭時距分布）已知的情況下，通過模擬乘客在公交網絡中的路徑選擇行為，推導出乘客在不同線網布局下的分布情況，從而得到各公交路段（或公交線路）的客流量和其他指標，據此用以指導實踐[4-5]。該問題的表象是乘客的宏觀出行現象，其結果是獲得公交系統內各公交路段（或公交線路）的客流量和其他指標，其核心則是如何描述乘客在公交網絡中各個OD對之間的路徑選擇行為，其目的是為了了解各OD對之間的客流量在公交網絡中各線路上（各公交路段上）的流動情況，并據此為公共交通線網規劃和場站布局提供重要的理論依據。因此，從本質上來看，公交客流分配模型就是在乘客路徑選擇的基準之上做出某種假設而進行的分析和求解[6]。

早在上世紀六七十年代，公交客流分配問題就受到了眾多學者的重視和關注：Dial等提出了“主干線路路段”概念；Chriqui等提出“公交共線”概念，解決了乘車點或換乘點如何選擇合適的吸引線路集問題，但得到的解并不是全局最優解；自上世紀80年代起，隨著人們對考慮擁擠效應的公交客流分配理論研究的逐步深入，均衡概念被引入到公共交通客流分配研究領域，文獻[7-9]中的研究都是基于確定型用戶均衡概念而建立的經典客流分配模型；文獻[10-15]中則是在隨機用戶均衡的基礎之上建立的客流分配模型；需要特別強調的是，在考慮車輛容量約束的前提之下，文獻[16-18]中分別建立了隨機用戶均衡客流分配模型，但各自的側重點有所不同：文獻[16]中強調動態性，文獻[17]中基于可靠性，文獻[18]中明確考慮了不舒適度，這些研究均屬于平衡客流分配模型的研究范疇。

為了使客流分配研究能更好地貼近實際，近幾年來關于非平衡分配原則的相關研究逐步被重視：Teklu等[19]巧妙地基于隨機過程方法建立了考慮嚴格安全容量限制的客流分配模型；Rouhieh等[20]基于馬爾科夫決策過程的公共交通系統自適應路徑選擇模型；Kurauchi等[21]采用吸收馬爾科夫鏈方法，考慮線路容量限制以及未能成功搭乘吸引線路集合中第1輛到達車輛的概率，建立共線條件下的客流分配模型；Hazelton等[22]對基于馬爾科夫鏈的交通分配模型的相關計算給出了詳細分析，并對其魯棒性進行了分析。

綜上所述，現有關于平衡和非平衡的公交客流分配研究取得了較快的進展和重要的成果，為本文研究奠定了基礎，但這些研究大多并未考慮換乘對公交客流分配造成的影響，也就忽視了由換乘帶來的出行成本增加而引起的乘客路徑選擇的多樣性和復雜性。而目前大城市中“城外居住，城內上班”現實需求導致的出行距離不斷增長而引起公交半徑的增加，有相當部分居民出行需通過中途換乘才可到達目的地，這就使得理論研究與生活實踐有一定的脫離，為了使客流分配模型能更好地貼近實際，有必要考慮換乘對公交客流分配造成的影響。因此，本文結合公交網絡的特殊性，提出了符合乘客路徑選擇行為的廣義公交路徑定義，并在此基礎上，重點分析了乘客的路徑選擇行為符合馬氏決策過程的“無后效性”，詳細給出路徑選擇過程中涉及的狀態-行動空間及狀態轉移概率，建立了基于馬爾可夫鏈的非平衡公交客流分配模型，并設計了相應的求解算法。最后，運用成都市部分公交網絡的實際運營數據對模型和算法進行實例驗證，并根據分配結果對相關參數進行了敏感性分析。

1 關鍵概念與問題描述

公交網絡由站點及連接站點的線段組成（線段是指相鄰2個站點之間的部分），每條線段都有一組公交線路（以后簡稱線路）經過，每條線路均有一定的發車頻率和服務類型，不同線路之間可能存在部分相同的線段，乘客只能在站點上下車或換乘其他線路。

對于大規模公交網絡而言，任意OD對之間連通的路徑通常有多條，但乘客并非考慮所有路徑，也不會總是單一地選擇最短路徑，如圖1所示。乘客有可能選擇直達路徑r0（換乘0次），也有可能選擇需要換乘1次的路徑r1，在某些情況下甚至可能選擇需要換乘2次的r2。部分站點離乘客的出發地較近，部分站點離乘客的目的地相對較近，部分站點可搭乘的線路相對較多，這些也都是影響乘客路徑選擇行為的關鍵因素。

圖1 共線情況下的乘客路徑選擇

通常情況下，乘客被認為是目標導向的理性個體，在面臨不同的交通環境時，有其各自不同的行為目標和行為準則，出行過程中他們不僅需對當前所處環境作出判斷與估計，還需對未來的狀態（如如果需要換乘，則應考慮選擇在哪個站點下車更便捷或更省時）進行預估，以求達到非合作情況下的個人目標最優（如最小化總出行成本、最大化在約束時間內到達的概率等），這就導致整個交通系統狀態的不確定性和難以預測性[23]。在這個實際背景下，基于換乘站點提出符合乘客路徑選擇行為的廣義公交路徑定義，研究考慮換乘行為的城市公交網絡客流分配問題，具有較強的理論意義和實踐價值。

2 理論分析及建模

2.1 廣義公交路徑定義

為避免降低可行換乘路徑的搜索空間，本文綜合考慮同步換乘（在下車站點即可搭乘需換乘的線路）和非同步換乘（乘客通過步行一段距離換乘的情況），將一定步行距離內可能換乘的多個站點抽象為1個站點對公交網絡進行拓撲建模，不同距離下的非同步換乘站點如圖2所示。

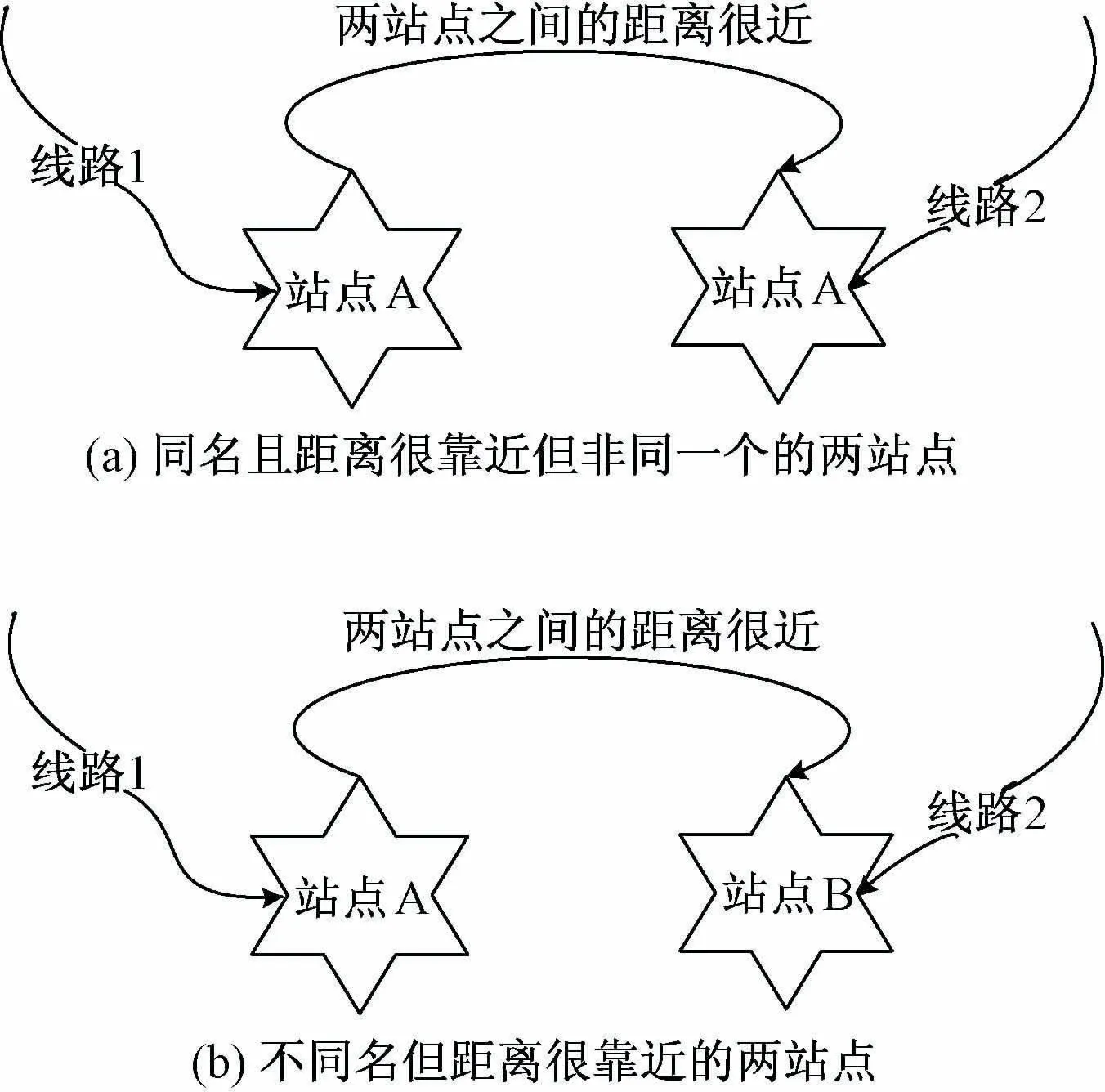
圖2 非同步換乘站點

針對公交網絡的特殊性，結合本文提出的換乘站點含義，定義符合乘客路徑選擇行為的廣義公交路徑為乘客從起點到達終點所選擇的換乘站點序列（簡稱路徑）。稱路徑上相鄰2個換乘站點之間的部分為公交路段（簡稱路段），路段通常包含1條或多條不同的線段。

簡單公交網絡與廣義公交路徑分別如圖3、4所示。由原來7條線路（l1，l2，…，l7）編碼的公 交網絡經由路徑編碼后，僅有3條路徑即可清晰描述：經過站點s1和s4的路徑r3，經過站點s1、s2和s4的路徑r4，經過站點s1、s3和s4的路徑r5。由路徑編碼的公交線網更加簡單明了，對于大規模公交網絡而言，該優勢將更加明顯。

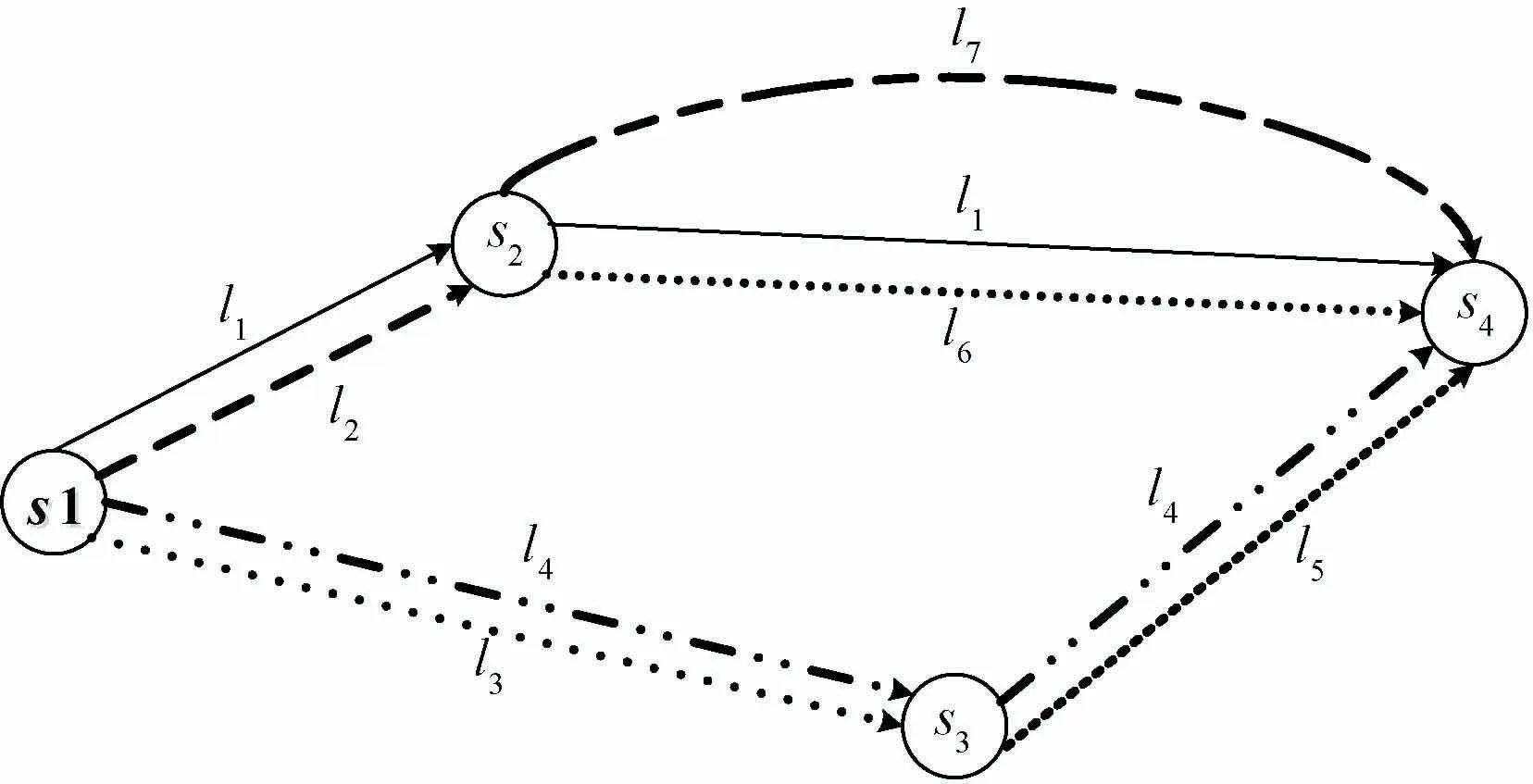
圖3 一個簡單的公交網絡

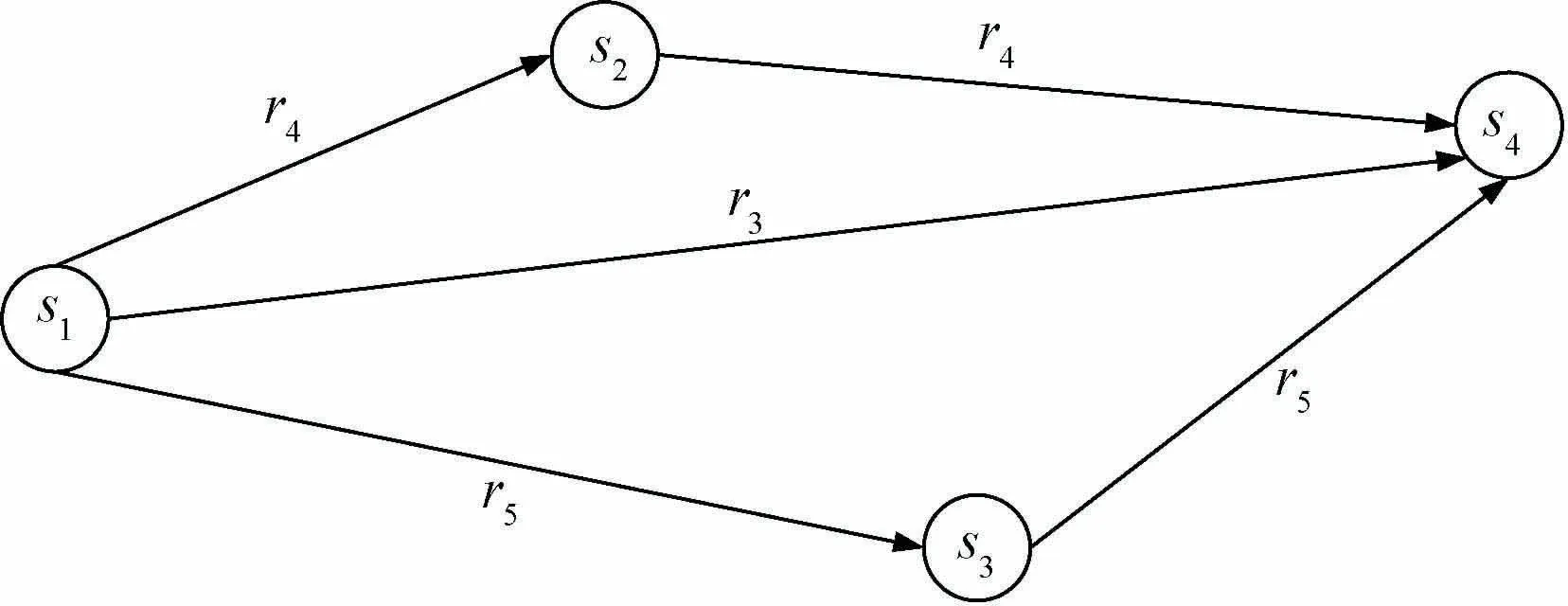
圖4 廣義公交路徑

2.2 馬爾科夫鏈的適用性

公交出行不同于個體交通（自駕車）出行，其自由度相對較小。通常情況下，尤其對常乘客而言，在每次出行之前乘客都會對當次出行有一定的計劃和預期，如根據各自的出行目的、出行距離及為出行預留的約束時間等，選擇相應的起點站、換乘站以及終點站等。根據廣義公交路徑定義可知，公交出行實際上是一組使得乘客從公交網絡的各個起始節點經由換乘節點到達終點的規則集合，因此，公交路網中客流量的分配過程，可看成是乘客從公交路網中的起點站出發，在各換乘站點按照一定的轉移概率選擇可行公交線路，最終到終點站的過程，該過程從廣義上來說滿足馬氏過程的無后效性。下面以乘客一次完整的公交出行（從家到工作地點的公交出行）為例對此過程進行數學描述和證明。

以乘客的地理位置轉移為切入點，如從家轉移到起點站，從起點站轉移到換乘站，從換乘站轉移到終點站等，在這一系列轉移過程中，乘客總是位于如圖5所示的這7個相互排斥但總體完備的狀態集合中的元素之一，且在每個狀態下都將面臨一組可能的行動，如表1所示，當處于“在家”狀態時，面臨出發時間和起點站的選擇，決策的執行使得乘客的狀態從“在家”通過步行或其他方式轉移到狀態“位于起點站”，該狀態轉移對應圖5中虛線框圈出的部分，表1列出了與圖5中7個狀態對應的所有可能的行動空間。需要特別指出的是，本文重點考察乘客的換乘行為，當乘客到達某一預期或預定的換乘站點時，無論在此之前的選擇如何，都不會對乘客在此換乘站點換乘哪條公交線路向目的地前進產生影響，這并不意味著之前的選擇不重要，而是當前選擇較之前的選擇對未來結果的相對影響更大，且在到達換乘站點之前的決策對當前結果的影響可通過乘客到達該換乘站點的時間和到達該換乘站點已支付的票價來體現。

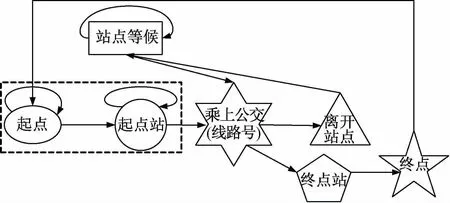
圖5 乘客路徑選擇狀態轉移圖

表1 乘客公交出行過程中的狀態及對應的行動

綜上分析，可將乘客的路徑選擇過程視為一個隨機過程，記為｛X（t），t∈T｝，令x0=在家，x1=向起點站行進，x2=站點等候，x3=公交車內，x4=換乘站點，x5=終點站，x6=到達目的地，其狀態空間為E，對

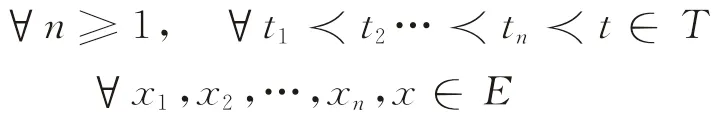
且X（t）在已知條件

下的條件分布函數只與X（tn）=xn有關，而與

無關，即條件分布函數滿足以下條件概率分布等式：

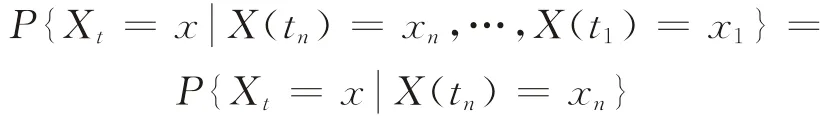
因此，基于乘客的換乘行為，從廣義上來說，給定乘客過去的狀態x0，x1，…，xn-1和現在的狀態xn（即到達換乘站點），將來狀態xn+1的條件分布獨立于過去的狀態，且只依賴于現在的狀態（目前所處的換乘站點），即乘客的路徑選擇行為滿足馬氏過程的無后效性，即｛X（t），t∈T｝為馬爾科夫鏈。

2.3 基于馬爾科夫鏈的公交客流分配模型

2.3.1 客流量的確定 對于給定的公交網絡G（N，A），S為站點集合（si∈S），假設起始站點為p個，終點站為q個，中間換乘站點（不包括起終點站）為n-p-q個，則乘客在整個公交網絡中各站點之間的一步轉移概率矩陣為

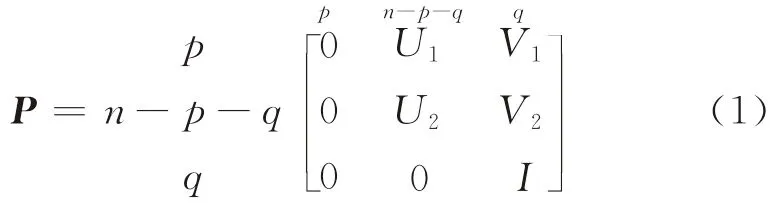
在定義了一步轉移概率矩陣P后，m步轉移概率為處于狀態i的過程在m次轉移后處于狀態j的概率

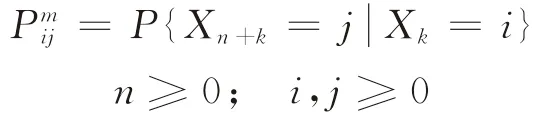
由C-K方程（切普曼-柯爾莫哥洛夫方程）可知

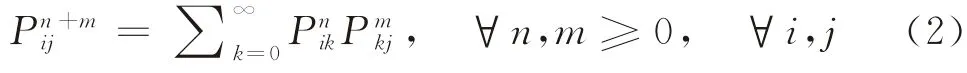
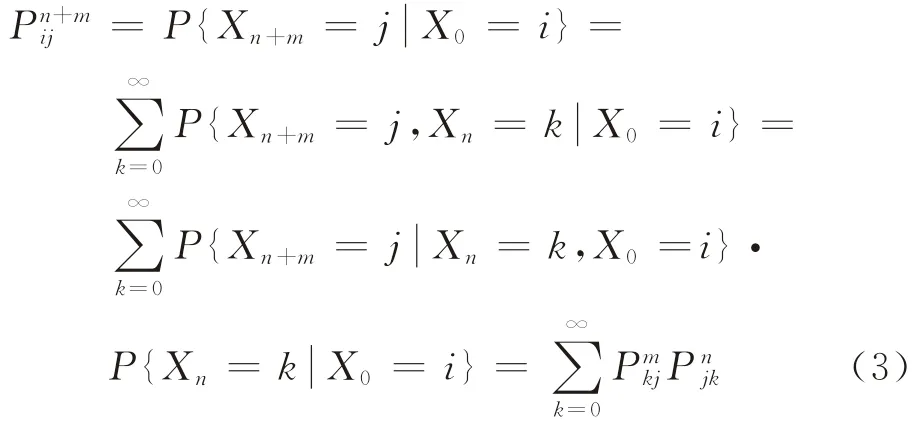
記P（n）為n步轉移概率的矩陣，由式（2）可得P（n+m）=P（n）P（m），特別地，P（2）=P（1+1）=PP=P2，故由歸納法可知

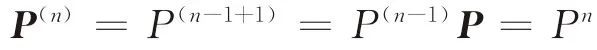
因此，矩陣p的m次冪矩陣為

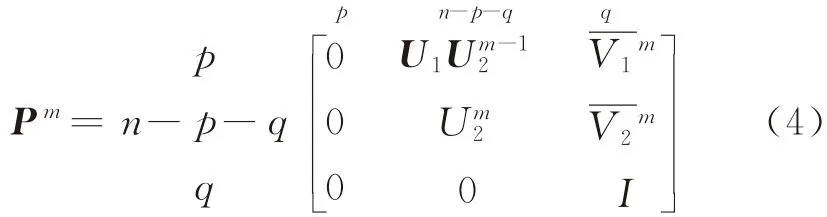
乘客通過選取各自的可行線路到達終點站，式（4）中，

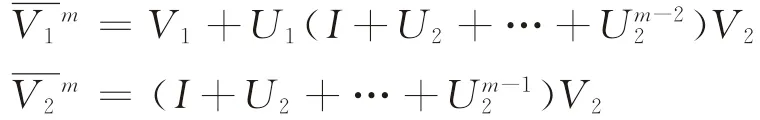
Pm的分塊矩陣中的元素（si，sj）為由起始站點si出發的乘客量經過m次轉移（即m次換乘）到達站點sj的概率，初始階段乘客位于各自的出發點，故m=0時，P0=I。若公交路網中所有乘客可行路徑的換乘次數最多為M-1次（即路段數目為M），則有=0，那么，由各起始站點so產生的客流量到達各中間換乘站點的概率為[24]。

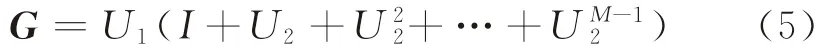
矩陣G中的元素（si，sj）為由站點si出發的客流量通過換乘站點sj的概率，由換乘站點的選擇概率和與之相關聯的路段選擇概率相乘便可得到乘客該次出行被選路段的選擇概率。因此，公交路網中路段（si，sj）的客流量為

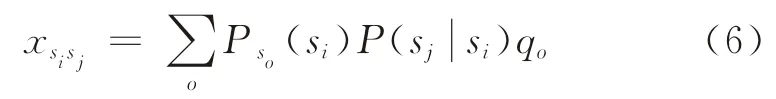
式中：Po（si）為由站點so出發的客流量通過站點si的概率；為乘客由站點si轉移到站點sj的概率；qo為由站點so出發的客流量。

2.3.2 廣義公交路徑下的轉移概率 現實生活中，尤其是大城市，“城外居住，城內上班”的現象十分常見。據此，本文選取早高峰期時段的一個多源單匯的公交網絡進行研究。根據廣義公交路徑定義，建立公交路網中由站點si途經路段（si，sj）到達站點sj的一步轉移概率函數為[24]

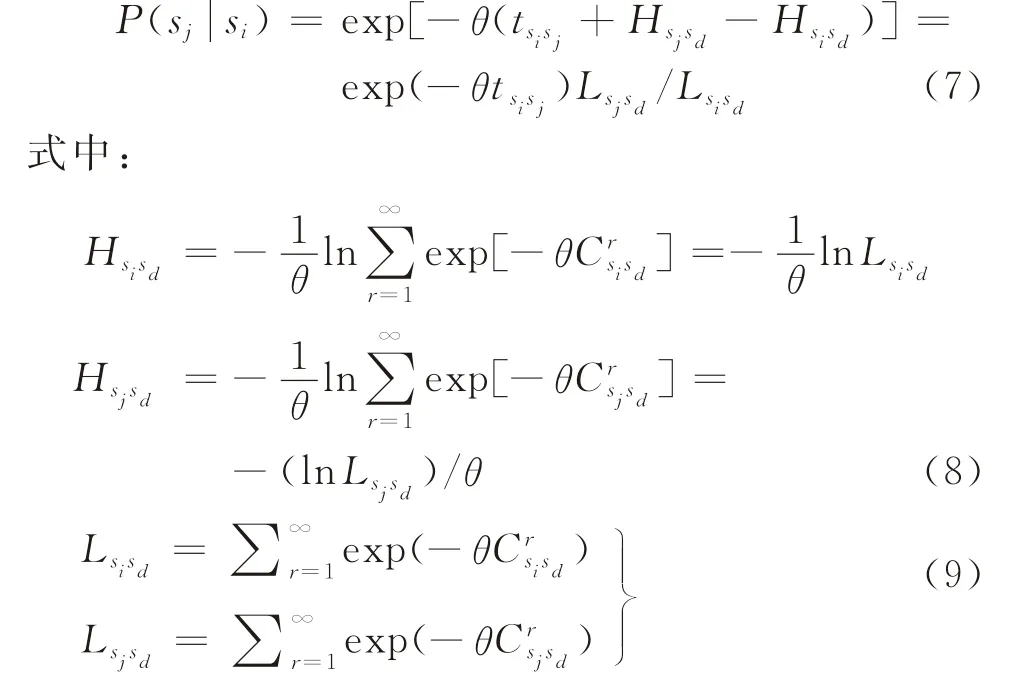
式（7）～（9）中，θ為給定的與路況相關的常數；Rsisd為由站點si到終點站sd的廣義路徑集合；Rsjsd為由站點sj到終點站sd的廣義路徑集合；tsisj為路段（si，sj）的行駛時間為由站點si到終點站sd的可行路徑第r條路徑的廣義出行成本為由站點sj到終點站sd的可行路徑第r條路徑的廣義出行成本。

由于

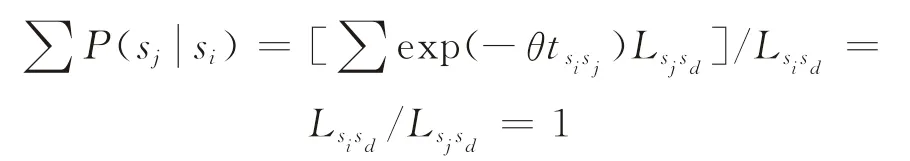
故式（7）給出的轉移概率滿足非負和歸一化條件。對于OD對sosd間乘客的某次出行，在已知出行路徑r的所有路段選擇概率條件下，r的選擇概率為

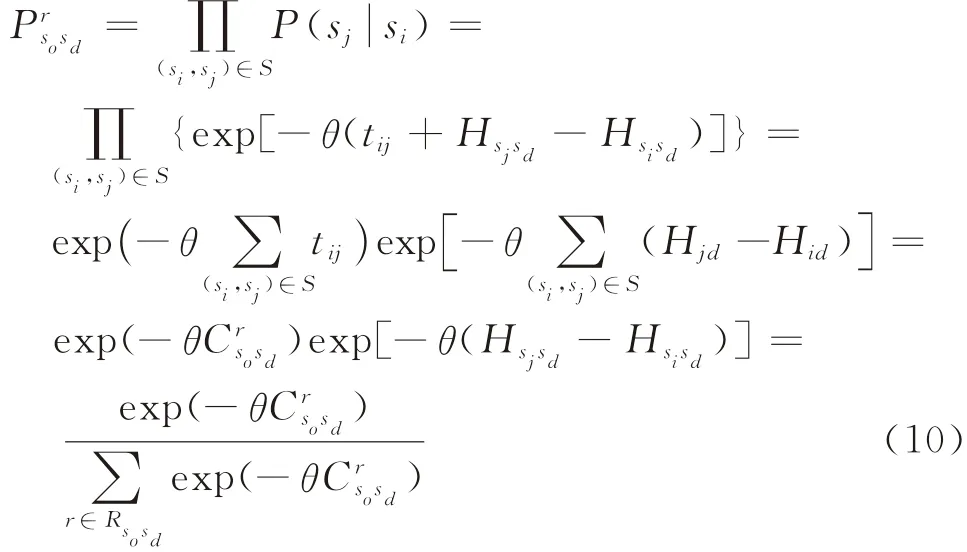
由式（10）可知，由轉移概率得到的路徑選擇概率與Logit配流模型的路徑選擇概率是一致的，需要說明的是，式（7）為前向條件轉移概率，對起始站點沒有任何約束，僅指定了一個唯一的終點站sd，故該轉移概率適用于多源單匯的公交路網，也就能滿足目前大城市“城外居住，城內上班”的居民出行需求分析。而對于單源多匯的公交路網，有如下的后向條件轉移概率定義：

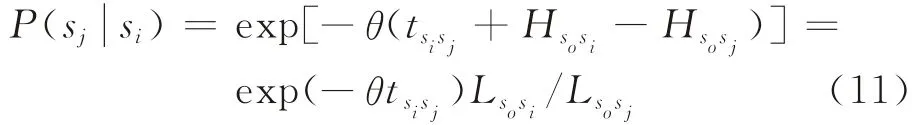
3 模型求解

為了計算轉移概率中的Lsisd、Lsjsd、Lsosi和Lsosj，針對一個n個站點的公交路網定義一個n×n矩陣A，如果站點si和站點sj之間有公交線路通過，則Asisj=exp（-θtsisj）；否則，Asisj=0，故式（12）成立。

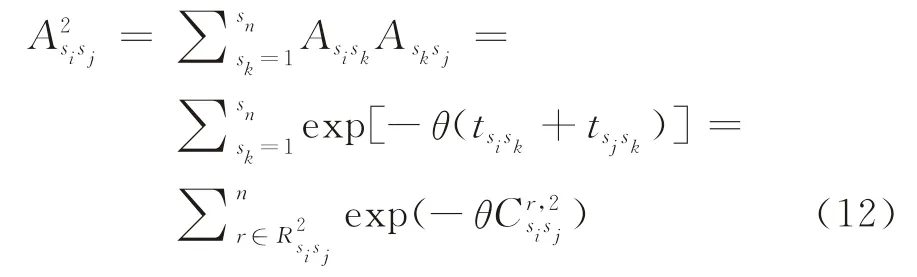
式中：為由站點si通過n條路段到達站點sj的所有路徑集合為中第r條路徑的廣義出行成本，同理可得

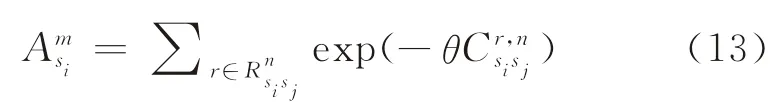
顯然，如果路網中任意兩站點之間的最多路段數目為M，則有AM+1=0。因此，式（9）的計算就等價于求解以下矩陣系列的和，即

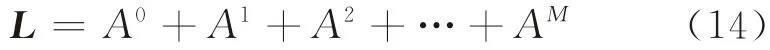
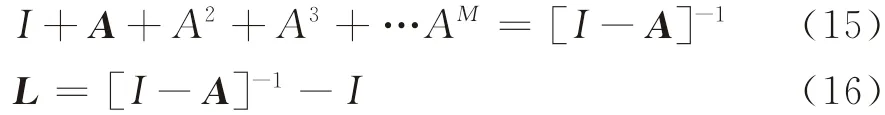
值得注意的是，當廣義公交路徑定義下的公交路網存在回路時，則路網中至少有2個站點之間的可行路徑數目為無窮大，由此，式（5）或式（14）中的最長路徑的路段數目M則為無窮大，故有

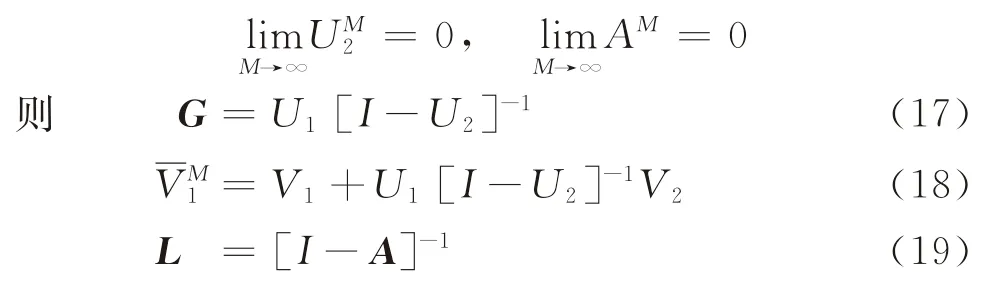
針對目前“城外居住、城內上班”的現實情況，下面著重分析多源單匯的公交路網，即對起始站點無約束而終點站相同的公交網絡（q=1），A矩陣具有如下特殊形式：

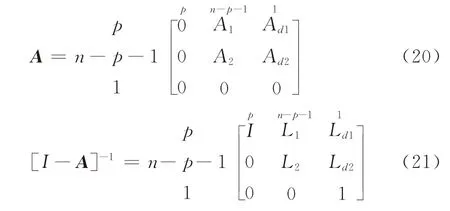
式中：

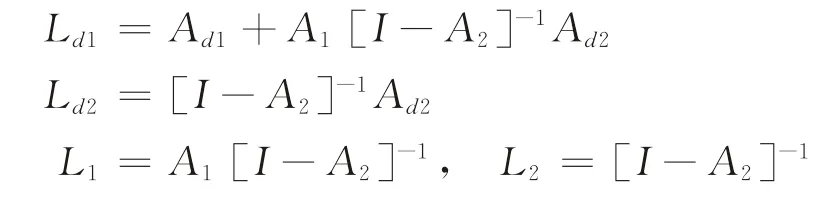
根據轉移概率定義，有

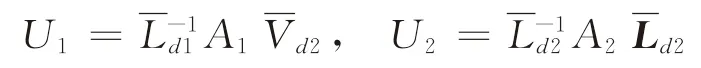
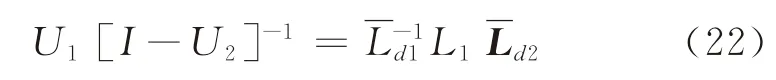
綜上分析可知，針對多源單匯的公交路網客流分配算法只需計算（n-p-1）×（n-p-1）的逆矩 陣[I-A2]-1，與 直 接 計 算[I-A]-1和[I-U2]-1相比，計算量將大大減少，下面給出具體的算法步驟：

（1）如果站點si和站點sj之間有公交線路通過，則Asisj=exp（-θtsisj）；否則，Asisj=0，據此構造A矩陣，然后由式（14）和式（16）計算L矩陣；

（2）由式（7）、（11）中選擇相應的一步轉移概率定義式，據此計算一步轉移概率矩陣P；

（3）再由式（5）或式（17）得到G矩陣；

（4）若已知或通過需求分析獲取OD出行量，由式（6）求得各路段上的交通量。

值得一提的是，若針對一般的多源多匯公交路網，根據分解原理，可將其分解為若干個多源單匯或單源多匯的子路網，這樣一來，式（7）、（11）所定義的轉移概率同樣也能適用。

4 應用算例

現實生活中，尤其是早晚高峰，城市公交網絡客流量大，換乘量也大，因此，本文選取成都市如圖6所示的6條公交線路：7路下行、28路下行、37路下行、56路下行、62路下行和101路下行，以九里堤公交站到新南門汽車站、西門車站到紅星路口和紅星路口到西門車站的出行為例，對模型和算法進行驗證，通過實際調研和分析可合理假設各路段阻抗值，如表2所示。

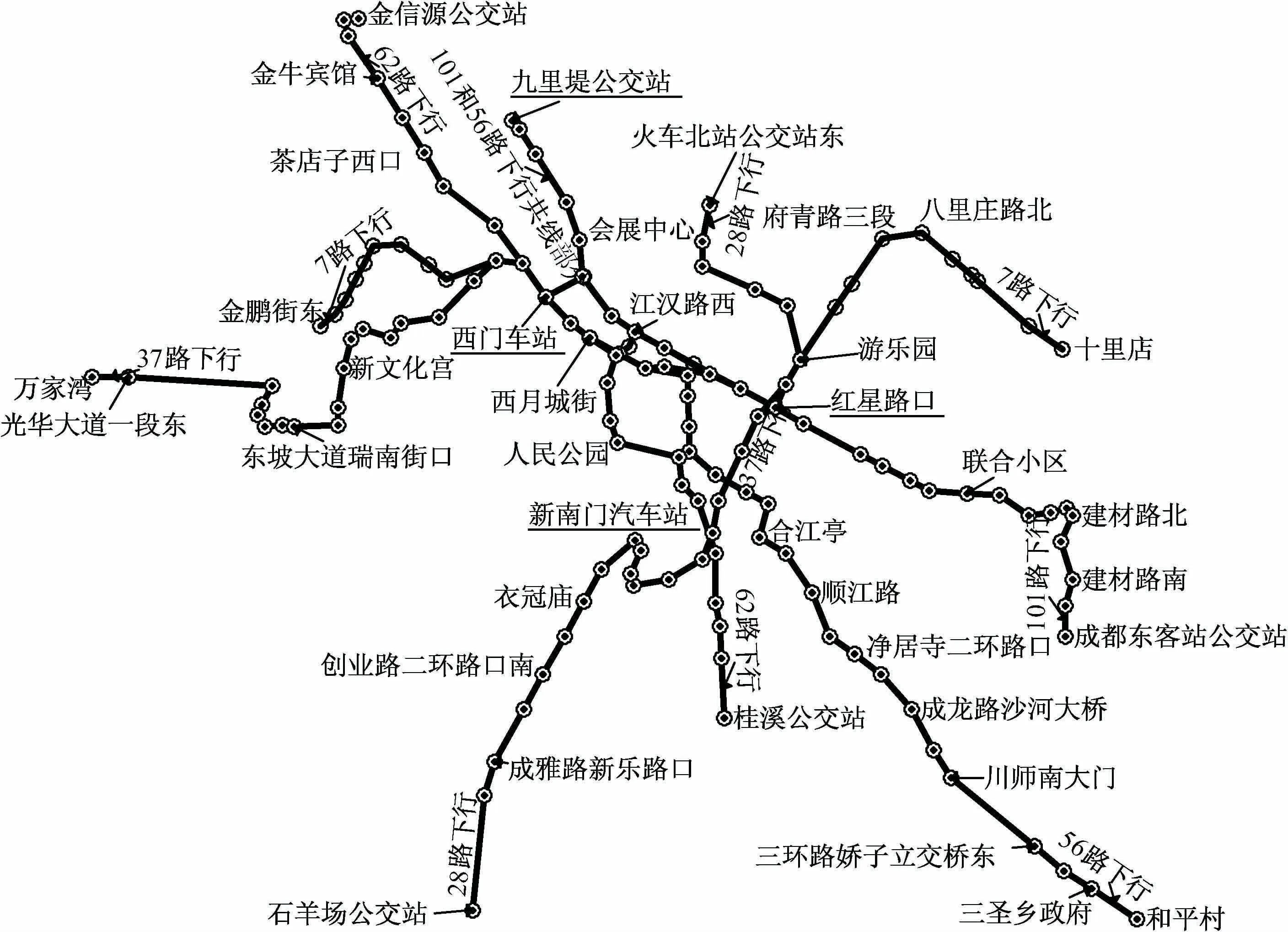
圖6 用于實例分析的真實公交網絡

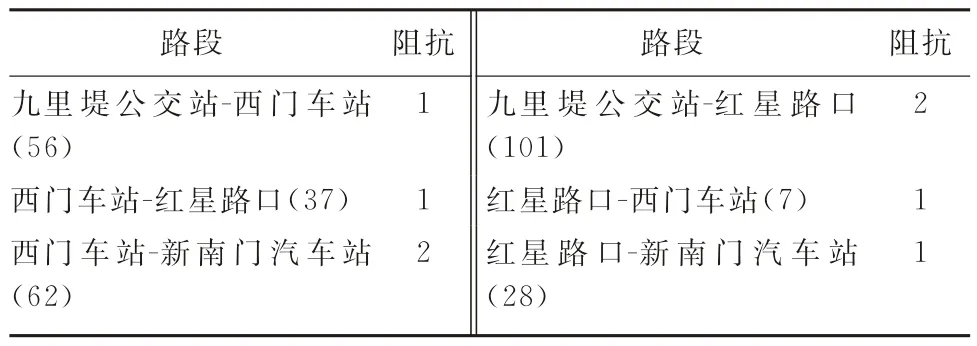
表2 各路段阻抗

各有效出行路徑描述如下：

（1）從九里堤公交站出發，乘坐56下行，經7站到西門車站下車，在西門車站換乘62下行，經10站抵達新南路站，向西北方步行221 m到達新南門汽車站；

（2）從九里堤公交站出發，乘坐101下行，經11站到紅星路口站下車，向西南方步行246 m在桂王橋南站換乘28下行，經2站抵達新南門汽車站；

（3）從西門車站出發，乘坐37下行，經8站即可抵達紅星路口站；

（4）從紅星路口站出發，乘坐7下行，經9站即可抵達西門車站。

將九里堤公交站、西門車站、紅星路口以及新南門汽車站分別編碼為O、1、2、D，令W=e-θ，如果站點si和sj之間有公交線路通過，則=；否則，=0，據此，構造圖6的 矩陣為

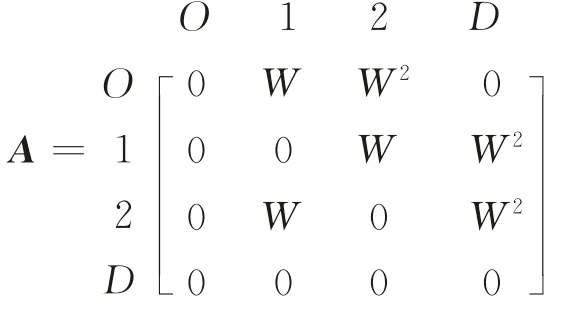
則有：

由式（22）可得西門車站和紅星路口的選擇概率：

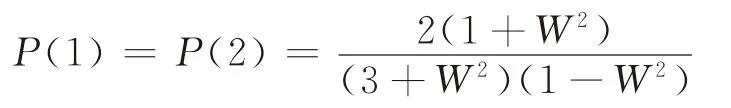
由式（19）、（20）計算矩陣：

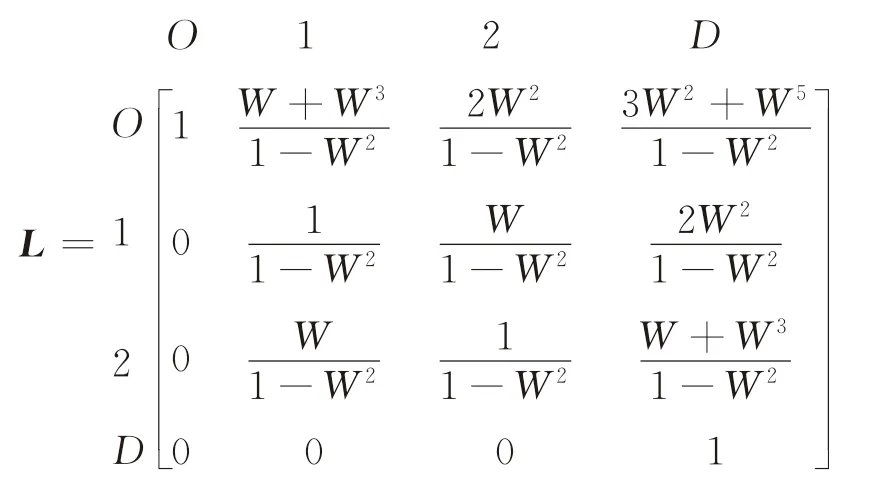
各站點之間的一步轉移概率可由式（7）分別求得：

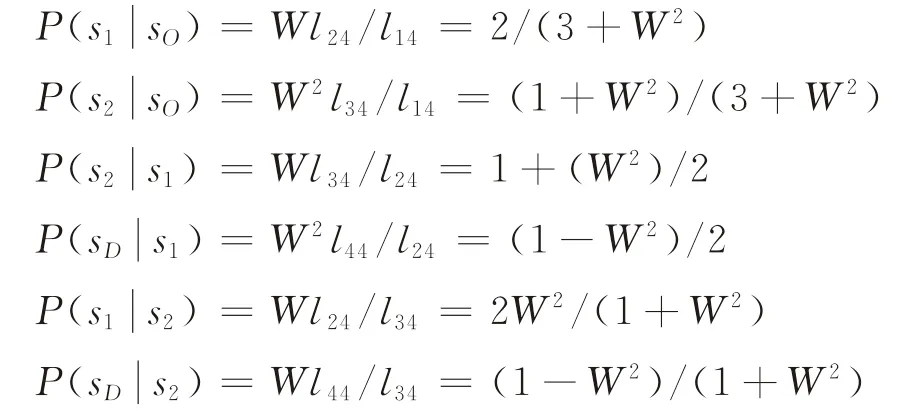
由式（17）可求得各換乘站（西門車站、紅星路口）的通過概率為：

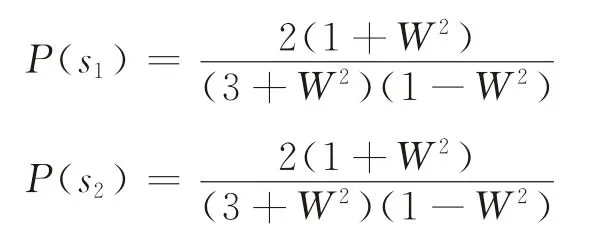
若從九里堤公交站出發的交通量為Q，則各路段客流量可通過式（6）進行計算。

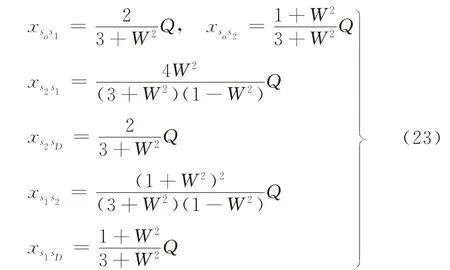
下面運用成都市公交的實際運營數據（數據概況見附錄）來檢驗模型和算法的可行性和有效性，對成都市IC卡消費數據進行統計分析，可合理假設各公交線路2012-06-12的客流量，如表3所示。

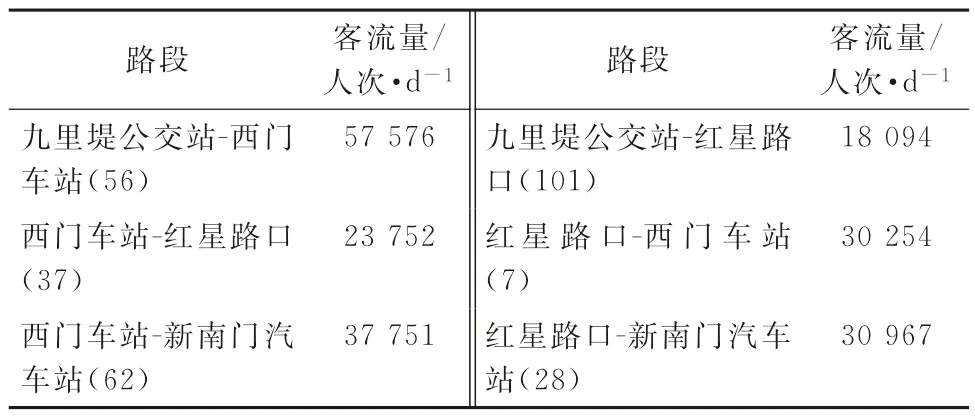
表3 以各公交線路2012-06-12的客流量作為各路段的客流值

據式（23）計算各路段客流值，對參數θ進行敏感性分析，考察不同θ取值情況下的客流分配結果（θ=1，θ=2，θ=10，θ=+∞），并對結果做出合理的解釋和說明，詳情如表4和圖7所示。

由圖7可知，即便是不同的θ取值，各路段客流分配的預測趨勢都是和實際情況較相符的，θ值越大，乘客對路網的熟悉程度越高，分配結果越接近實際，這也是很合理的，從而能從一定程度上驗證模型和算法的可行性和有效性。

表4 各路段客流分配結果

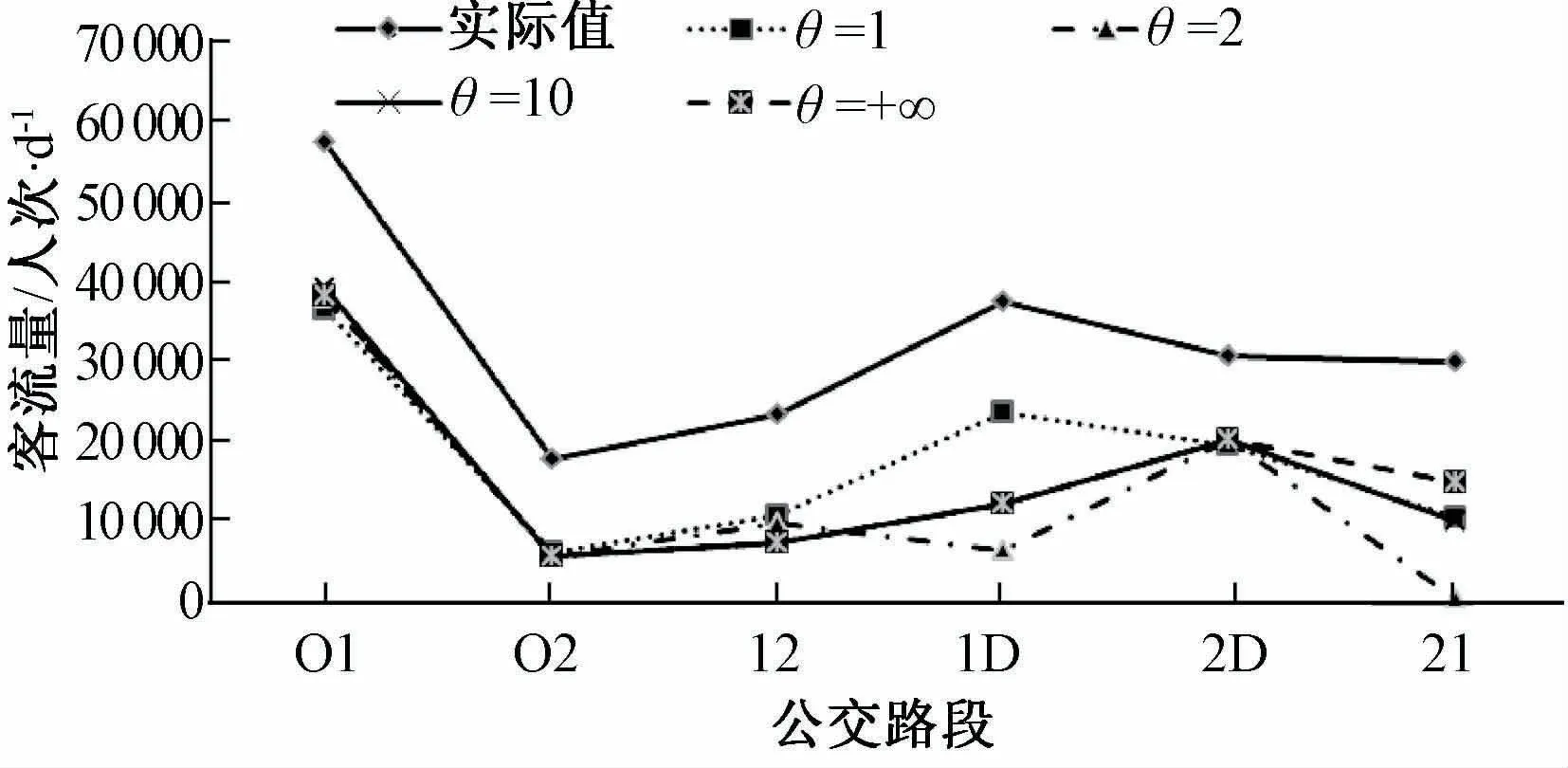
圖7 參數敏感性分析

5 結語

本文針對中國大城市“城外居住，城內上班”的工作生活模式與公交網絡的特性，基于換乘站點，提出了符合乘客路徑選擇行為的廣義公交路徑定義，將馬爾科夫決策過程與乘客的路徑選擇行為聯系起來，證明了由轉移概率得到的路徑選擇概率與廣義路徑下的Logit配流模型的路徑選擇概率是一致的，為解決考慮換乘問題的客流分配問題找到了較好的突破口。本文研究為公交網絡規劃、城市公交網絡設計及優化等提供了一定的理論基礎。但是，實際問題的復雜化和模型的抽象化使得本研究存在一些不足之處，若能將GPS數據與IC卡消費數據進行匹配，準確掌握各個時段各個路段的客流量，在此環境下，研究考慮換乘行為的公交客流分配問題更具現實指導意義，深入分析和研究該問題是下一步將要進行的工作。

附錄

（1）成都市公交數據概況。截至2012年初，成都市公交集團運營路線已達到323條，成都中心城區平均每天服務乘客達到373萬人次，高峰時段的日均載客量已經突破400萬大關，IC卡發卡量也由85萬張激增至600多萬張，中心城區日均出行的分擔率已經從2007年的14.7%上升到目前的24.18%。

（2）公交數據庫基本表的字段說明。成都市IC卡消費數據庫中各個字段表征的含義如附表1～4所示。

附表1 公交卡的基本類型

附表2 公交卡充值數據表

附表3 刷卡消費數據表

附表4 車載GPS數據表