引發認知沖突 促進概念理解
吳瑞英
[摘 要]數學教學中,教師應以學生的認知為切入口,設置符合學生實際的認知沖突,激發學生的學習動機與需求,使每位學生都深刻理解所學知識。
[關鍵詞]數學教學 認知沖突 概念 理解 促進
[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068(2015)20-043
“認識分數”既是教學分數的第一課時,又是學生學習分數概念的起始課。因此,教師在教學中要根據學生的認知特點,合理設置認知沖突,促進學生對概念的理解,這對學生掌握分數的本質至關重要。
一、創設情境,感知概念
學生學習數學是從自己的生活實踐開始的,因此教師可以創設貼近學生生活的情境,激發學生的探求欲,引導學生通過觀察、想象等活動,逐步感知概念。
教學片斷:
師:剛才我們很順利地把四個蘋果和兩瓶水進行了平均分,那你們會分蛋糕嗎?
生1:我會平均分,要公平,每人一半。
師:每人一半,大家同意這位同學的意見嗎?(同意)那“一半”如何用數來表示呢?(學生討論)
生2:老師,“一半”可以用二分之一來表示。
師:二分之一?請你上來寫一寫。(生上臺板書1 / 2)
師:這個二分之一,我們以前沒接觸過呀!那你知道1 / 2是什么意思嗎?
……
反思:上述教學中,教師先喚醒學生已有的平均分知識,使學生的思維順著平均分很自然地想到把一個蛋糕平均分才公平,這樣就將分數最本質的特征“平均分”在不露痕跡中讓學生感知了。“那‘一半’如何用數來表示呢”,這是學生認知的第一次沖突,從自然數到分數,既是對數的擴充,也是學生認識自然數后的一次知識“生長”。學生嘗試用數來表示“一半”,從而經歷了一個思考、創造的過程,對分數的初步感知會更加深刻。
二、動手操作,深化概念
小學生學習數學的過程,就是自己“做”數學的過程。為了幫助學生深化對概念的認知,可將形成分數概念的過程變為在嘗試操作下的思考與分析的過程。
教學片斷:
師:拿一張長方形紙折一折,并把它的1 / 2涂上顏色。(學生先動手操作,再交流展示不同的折法:一是沿兩條長的中心對折;二是沿兩條寬的中心對折;三是沿對角線對折)對這三種不同的折法,你有什么想說的?
生1:我覺得這三種折法都對,都是表示這個長方形的1 / 2。
生2:我也覺得是對的,只是好像有什么不同的地方。
師:什么地方不同呀?
生3:平均分后的形狀不同。
師:平均分后的形狀不同,為什么都可以用1 / 2來表示?
生4:雖然形狀不同,但它們都是把長方形紙平均分成兩份,一份就是它的1 / 2。
……
反思:上述教學中,教師先讓學生自己動手折,展示不同的折法,再讓學生自主探索,并對結果進行思辨,從而產生第二次認知沖突——“為什么形狀不同,都可以用1 / 2來表示”。“雖然形狀不同,但它們都是把長方形紙平均分成兩份,一份就是它的1 / 2”,學生此時對分數的本質屬性的認識就有了一個質的飛躍。
三、變式比較,內化概念
“形成數學概念的標志就是掌握對象的內涵與外延。”課堂教學中,教師要通過呈現不同的變式,引導學生從拓展分數的外延來內化概念的內涵,為學生順利、正確掌握分數的概念打下基礎。
教學片斷:
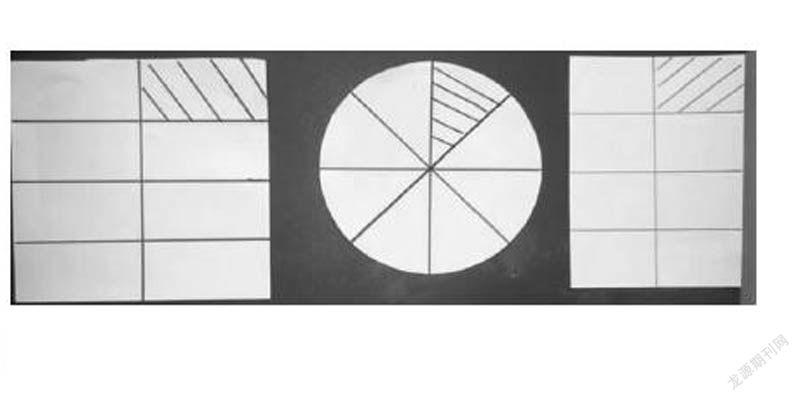
師(出示右圖):同學們,對于這幅作品,你有什么想說的?
生1:這幅作品都是把每個圖形平均分成8份,一份就是1 / 8。
師:不同圖形都可以得到1 / 8,這說明什么?
生2:說明分數的得出不是看圖形,而是看平均分的份數。
……
反思:經驗有時對概念的學習會產生消極的負效應。上述教學中,教師針對學生的思維定式,引導學生用不同圖形折出相同的分數來拓展分數的外延,創設第三次認知沖突——“不同圖形都可以得到1 / 8,這說明什么”,為學生形成正確的概念做好知識的鋪墊。
總之,教師在教學中應以學生的認知為切入口,設置符合學生實際的認知沖突,激發學生的學習動機與需求,使每位學生都深刻理解所學知識。
(責編 杜 華)

