量子力學中庫侖勢場問題的課堂教學設計

孫運斌

（內蒙古科技大學包頭師范學院物理科學與技術學院內蒙古包頭014030）

量子力學中庫侖勢場問題的課堂教學設計

孫運斌

（內蒙古科技大學包頭師范學院物理科學與技術學院內蒙古包頭014030）

本文對量子力學庫侖勢場問題求解過程進行了匯總，將數理方法中相關方程求解過程整合進入庫侖勢場問題求解過程，并對與求解物理問題關聯性較小的環節進行精簡，保留與具體物理問題求解關系較為緊密的部分并進行深入討論。論文對于增進學生對該問題求解過程中物理量間關聯的理解、提升課堂教學效果具有較為重要的意義。

庫侖勢場問題是量子力學課程中重要的教學內容，也是教學難點之一。[1,2]由于該問題求解過程涉及到的數學問題較為繁雜，實際教學過程中一般將求解過程提前在數學物理方法中進行，在量子力學課程中直接引用數理方法中給出的結論。[3]這一教學方式優點在于極大地提高量子力學教學的效率，加快課程進度；而其缺點在于數理方法在實際教學過程中一般前置于量子力學課程，因而在學生學習相關方程求解求解過程時并不能很好地理解各個參數的物理意義，因而對于各個物理參數的依賴關系尤其是主量子數、角量子數與磁量子數間的取值依賴關系難以形成直觀的認識。為解決這一問題，本文對庫侖勢場問題求解過程進行精煉，將整個求解過程壓縮

至可接受的教學課時量，并盡可能保留與實際問題關聯緊密的過程，以期提升該章節的課堂教學效果。

一、極坐標庫侖勢場問題及分離變量

在球極坐標體系下，庫侖勢場的薛定諤方程為：

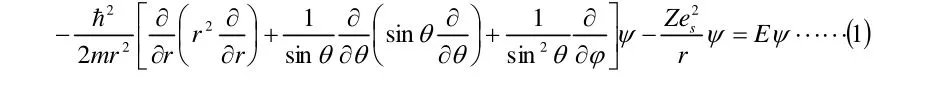
其解應為r,θ和φ的共同函數Ψ(r,θ,φ)，如這一函數可以描述為r的函數即徑向函數R(r )與θ,φ的共同函數Y(θ,φ)乘積的形式，即方程可分離變量為：

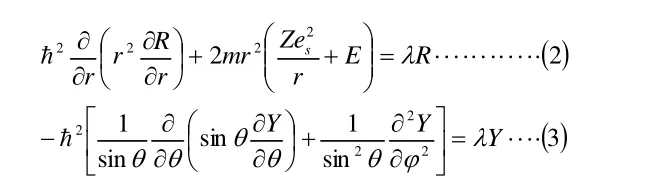
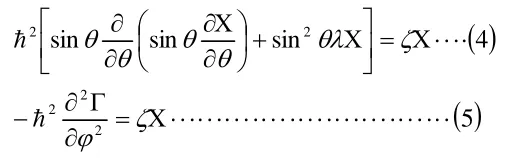
二、函數的求解

1. Γ()φ函數的求解

很顯然（5）式的解為：

2. Χ(θ)函數的求解

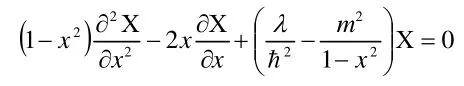
此方程稱為連帶勒讓德方程，其中當m=0時，稱為勒讓德方程。一般求解過程是先求解較為簡單的勒讓德方程，再求解復雜的連帶勒讓德方程。在本問題中，為體現角動量平方與角動量z分量的關聯，我們直接求解連帶勒讓德方程，勒讓德方程的解可以將m=0代入結果中給出，為實現對這一方程的求解，我們需對Χ函數進行如下代換：

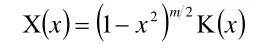
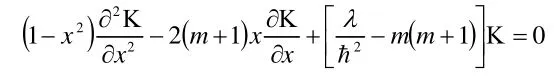
代入上式并整理同冪次項得：

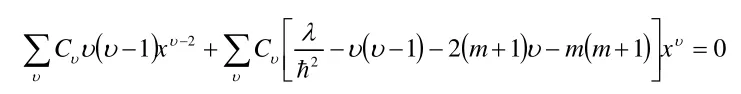
進一步簡化為：

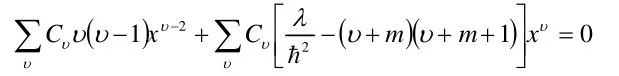
冪級數求和等于零，要求各個冪次的系數進行求和后均為零，因而不難看出由Κ(x)展開的級數冪次系數應滿足如下關系：

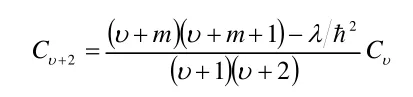
由級數的收斂判據可以判斷，該級數收斂半徑為1，且在收斂半徑上不收斂。而其變量x的取值范圍為，很明顯，在x=1即時，函數不收斂，因而，要獲得滿足有限性條件的函數，必須另此級數在某一項以后均為零，使級數截斷為多項式，相關的討論我們在處理一維線性諧振子問題時已經進行過討論，即使所有奇次冪項系數均為零，偶次冪項從某一項開始更高冪次系數為零；或所有偶次冪項系數均為零，奇次冪項從某一

項開始更高冪次系數為零。由上式可以看出，另υ+2次冪項系數Cυ+2為零的條件為：

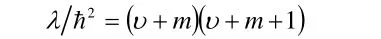
即

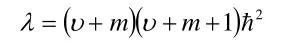
其中υ為奇數展開的冪次，只能為0或正整數，而m為磁量子數，只能為整數，因此λ的取值只能取? 2乘以某一整數乘以這一整數加1的倍數這一形式，我們將這一整數稱為角量子數，即為l，則有：

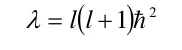
當確定了λ或角量子數l的取值后，Κ(x)函數的形式即可得以確定，即一個最高冪次為l，且僅包含奇次冪或偶次冪的求和多項式。該多項式的計算方法十分簡便，對于一個角量子數l與磁量子數m已給定的狀態。我們可以假設最低冪次即0次冪項或1次冪項系數為1，利用Cυ+2與Cυ間的遞推關系逐項進行遞推，直到遞推到l次冪項系數即最后一項非零項的系數為止。再將Κ(x)函數乘以(1-x2)m2即可得Χ(x )函數，將變量x替換回cos(θ)可得Χ(θ)函數，在于關于φ的函數乘積并進行歸一化，即可得算符的本征函數Ylm(θ,φ)，其中下標lm代表這一函數的形式取決于角量子數與磁量子數，由數學物理方法中已學習到，這一函數稱為球諧函數。球諧函數既是角動量平方算符與角動量z分量算符的共同本征函數，也是庫侖勢場問題波函數的角度部分。

關于角量子數l，有兩點需要注意：

第一點：將l與-l-1代入方程所得結果完全相同，即l可以作為一個負

第二點：當l取一正整數值時，由于冪次υ僅能取0或正整數，m取值應小于或等于l，否則無法獲得滿足有限性的解，即必須有m≤l；當m為負值時，函數有有限解的條件并為約束m絕對值的取值，但從物理量關系角度來看，當m絕對值大于l，即時，必有m2＞l(l+1)，因而會出現角動量z分量平方大于角動量平方的情況，而角動量x分量和y分量的平方只能為0或正數，因而從物理量關系角度而言，磁量子數m的絕對值絕不能大于角量子數l。

3. 即徑向函數R(r)的求解

對于徑向函數的求解，一般量子力學教材進行了較為完整的推導與證明，在此僅對針對角量子數l與主量子數n間聯系的部分進行重點討論，對于（2）式所示的徑向方程，當進行以下常量、變量及函數的代換，

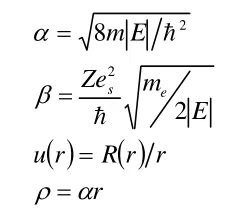
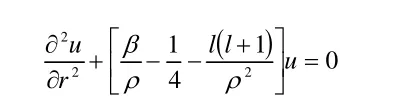
注意當ρ→0時，如果如果u(r )函數不比1r函數更快地趨向于0的話將會導致R(r)在r=0位置處取值為無限大，因而當ρ→0時，u(r)函數必須趨向于0。利用波函數有限條件，可以得到在ρ→∞與ρ→0時，方程的趨近解分別為：

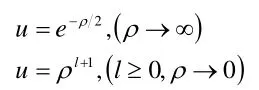
這里注意到，角量子數l，此時是作為ρ→0時函數的冪指數出現的，當然我們可以將l取為負值并將ρ→0時函數的趨近行為描述為：

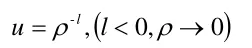
但很明顯，這一描述并不會改變問題的本質，即與量子數l相聯系的現象為：

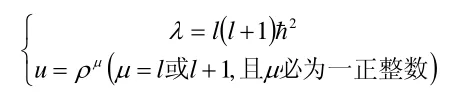
院

[1]量子力學教程(第二版)周世勛陳灝北京：高等教育出版社2009

[2]量子力學教程曾瑾言北京：科學出版社2003

[3]數學物理方法喬文華張占山趙建軍呼和浩特：內蒙古大學出版社2007

孫運斌男博士講師1984年4月出生

院