含左手材料與Kerr 非線性不定介質缺陷層一維光子晶體雙穩(wěn)態(tài)位移的動態(tài)調制

孔猛

（北京師范大學珠海分校工程技術學院北京519087）

含左手材料與Kerr 非線性不定介質缺陷層一維光子晶體雙穩(wěn)態(tài)位移的動態(tài)調制

孔猛

（北京師范大學珠海分校工程技術學院北京519087）

根據傳輸矩陣法和穩(wěn)態(tài)相位理論，在五個不同的頻率范圍內研究光束在含左手材料與Kerr非線性不定介質缺陷層一維光子晶體中的非線性傳播特性。結果表明：當非線性不定介質缺陷層為cut-off和never cut-off介質時，透射光強隨入射光強的變化呈S-型曲線關系，也就是說透射光強與入射光強存在光學雙穩(wěn)態(tài)特性。同時，透射光束的橫向位移隨入射強度也呈現出回滯曲線響應關系，并且通過改變入射光束的頻率，可以實現一維光子晶體橫向透射位移的動態(tài)調制。

一維光子晶體非線性不定介質雙穩(wěn)態(tài)位移

一堯引言

隨著人造媒介的發(fā)展，特別是超常材料（metamaterials）[1]的出現大大的拓展了電磁材料的特性研究。典型的超常材料如介電常數ε和磁導率μ同時為負值的負折射率材料，因為電磁波在這種材料中傳輸時其波矢→，電場→和磁場→形成了左手關系[5]，故又稱為左手材料（left-handed materials）。電磁波在左手材料中傳輸時會出現許多反常物理現象，如負折射率、逆Doppler效應、逆Cherenkov效應和完美透鏡等[2]。值得關注的是，D. R. Smith等[3]首次發(fā)現各向異性的特異材料——不定介質（indefinite metamaterials），不定介質這一新型材料立即成為物理學，微電子學以及信息技術等領域的研究熱點。

近年來，隨著對GH（Goos-H?nchen）位移[4]研究的深入，非線性GH位移亦引起了廣泛關注，如O. Emile等[5]在實驗上探測到自聚焦Kerr非線性介質界面處的非線性GH位移，Y. S. Kivshar等[6]研究了空間光孤子在向列液晶表面處的非線性GH位移特性，P. Hou等[7]研究了含通常Kerr非線性缺陷一維光子晶體雙穩(wěn)態(tài)位移的特性等。本文研究光束在含左手材料與Kerr非線性不定介質缺陷層一維光子晶體中的非線性傳播特性，分析入射頻率對雙穩(wěn)態(tài)位移的影響。

二、物理模型與推導

考慮一個對稱的多層膜結構(AB)mANA( BA)m作為一維有限維光子晶體結構，晶體兩側的對稱介質C(εC,μC)為右手線性材料。A(εA,μA)為右手線性材料，B(εB,μB)為左手線性材料，N(?N,?N)為非線性不定介質，m為周期數。介質層A，B和N的幾何厚度分別為dA，dB和dN。由于非線性各向異性超常材料的介電常數ε?N和磁導率μ?N是二階張量，為使討論的問題簡化，D. R. Smith等[8]假定材料的結構參數ε?N和μ?N可以同時對角化。在這種情況下，介電張量和磁導率張量可分別表示為：

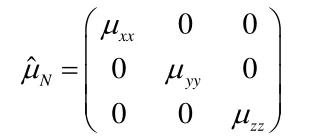
其對角分量εxx可以表示為，ε和χ分別為該分量的線性介電

x3常數和Kerr非線性系數。為簡單起見，我們忽略非線性材料的吸收特性。εx，μyy和μzz的色散關系可通過Drude模型來描述，即：（2）

其中Ω=ω/ ωp為歸一化的入射光頻率，Ωry=ωry/ωp和Ωrz=ωrz/ωp分別為y方向和z方向上的歸一化磁共振頻率，ωp為電等離子頻率，Fy和Fz分別表示開口環(huán)諧振腔在y方向和z方向所占區(qū)域的比例系數。

假設一角頻率為ω的平面電磁波從左側各向同性均勻右手材料中以入射角θ0入射到光子晶體中。我們假定入射電磁波的波矢位于y-z平面，入射電磁波的電場可以表示為，其中β和k分別是入射電磁波Cz波矢在分界面y方向和z方向的分量，。這里我們只考慮TE偏振波，對于TM偏振波的處理方法類似。

根據Maxwell方程組及邊界條件，相鄰任意兩層的電場分量和磁場分量可以通過傳輸矩陣相連接[9] 。對于Kerr非線性不定介質層，傳輸矩陣可表示為：（3）

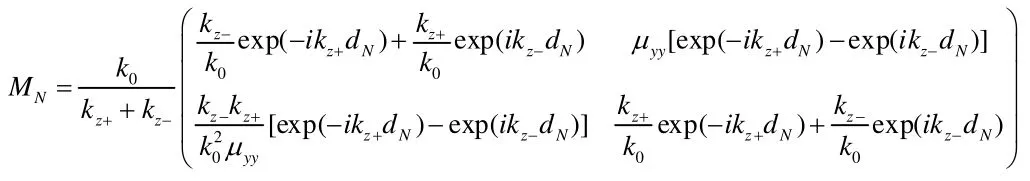
式中，kz+和kz-分別為前向波和后向波波矢在z方向上的分量，且他們均依賴于前向波和后向波的電場強度U±，即：（4）

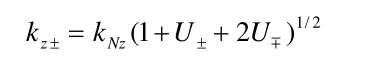
+-Nz不考慮非線性效應時缺陷層中電磁波波矢在z方向上的分量，滿足以下形式：（5）

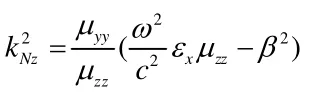
這里要注意的一點是kNz的符號必須與μyy保持一致[10]。

對于一給定參數的透射強度，我們可采用定點迭代法[11]求解一組關于U±的非線性耦合方程，便可以得到Kerr非線性不定介質層傳輸矩陣MN的具體形式。利用傳輸矩陣法，可以得到透射系數：（6）

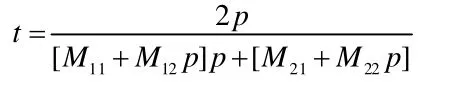
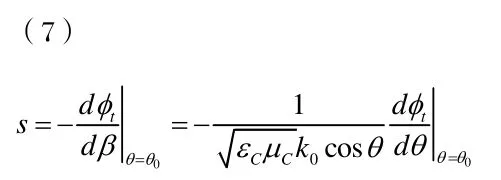
三、數值計算與分析

由式（2）可知，通過調整相應的結構參數與入射光頻率，可以在不考慮非線性效應的情況下實現對不定介質張量元εx，μyy和μzz正負符號的轉換。從式（5）可看出，正是由于張量元εx，μyy和μzz不同符號的組合，使得這種材料的色散關系或者為橢圓關系，或者為雙曲線關系。因此不同類型的Kerr非線性不定介質將會對一維光子晶體的電磁傳播特性產生不同的影響。在計算中，各物理參數選擇如下：對于Kerr非線性不定介質N[13]，Fy=0.56，Fz=0.78，ωp/2π=18.4GHz ，ωry/2π=ωrz/2π=15.3GHz，χ3=0.01，對于線性材料A，B和C[14]，εA=5.29，εB=-2.46，εC=6.25，μA=μC=1.00，μB=-1.00，m=3。Kerr非線性不定介質的張量元εx，μyy和μzz均與入射頻率有關，在不同的入射頻率范圍內這些物理量有著不同的符號，為了更明確地研究光束在含左手材料與Kerr非線性不定介質缺陷層一維光子晶體中的電磁傳播特性，接下來我們將在五個不同的入射頻率范圍分別進行討論。

（i）0＜Ω＜0.8315，此時εx＜0，μyy＞0，μzz＞0，即always cut-off 介質的一種情況。在這種情況下，kN2z總是負值，任何電磁波都不會透過這種介質板，而是被全部反射回來。

（ii）0.8315＜Ω＜1，這里εx＜0，μyy＜0，μzz＜0，此時當入射角θ0滿足θ0＜θc=arcsin時，由式（5）可知，波矢kNz為實數。那么，電磁波便可以透過含此類型的非線性不定介質的一維光子晶體。這種材料是cut-off 介質的一種情況，在不考慮Kerr非線性效應時，具有負折射效應。

（iii）1＜Ω＜1.2536，這里εx＞0，μyy＜0，μzz＜0，即always cut-off 介質的另一種情況，電磁傳播特性與（i）類似。

（iv）1.2536＜Ω＜1.7728，這時εx＞0，μyy＞0，μzz＜0，在這種情況下，kN2

z總是正值，任何電磁波都可以在含這種never cut-off非線性不定介質的一維光子晶體中傳播。因此，當光束以任何角度入射到這樣的一維光子晶體時，均可以產生透射位移。

（v）1.7728＜Ω，此時εx＞0，μyy＞0，μzz＞0，即cut-off 介質的另一種情況。當入射角θ0滿足條件θ0＜θc=arcsin時，由式（5）可知，電磁波同樣也可以透過含此類型的非線性不定介質的一維光子晶體。

下面，我們針對（ii）,（iv）,（v）三種情況下的非線性傳播特性分別進行詳細討論與分析。

3.1 0 .8315＜Ω＜1（εx＜0，μyy＜0，μzz＜0）

當Kerr非線性結構作為缺陷嵌入到一維光子晶體的中間時，禁帶中相應出現缺陷模頻率。由于缺陷層中強烈的非線性效應，導致缺陷模頻率隨入射光強度

的改變發(fā)生移動，當缺陷模頻率與入射光頻率接近時，產生雙穩(wěn)態(tài)現象[15]。數值計算中，我們采用的參數為：θ0=20°，ω/2π=16.07GHz ，

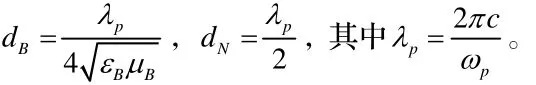
根據穩(wěn)態(tài)相位法分析，曲線的斜率表明透射光束的雙穩(wěn)態(tài)GH位移為負值。在一個非常狹窄的β區(qū)間內（β/k0=0.8551），當入射光強度在[1.31500,1.40600]區(qū)間內增大時，曲線斜率突然變陡，表示透射光束的GH位移S在高閾值點2處發(fā)生躍變，下跳到一個較大值；當入射光強度在區(qū)間[0.04092,0.02669]內減小時，曲線斜率發(fā)生躍變，即S在低閾值點1處達到負最大，然后上跳到一個較小值。

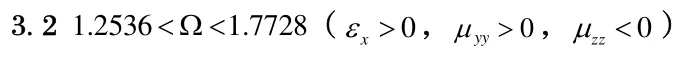
此時一頻率為ω/2π=25.17GHz的平面電磁波從左側各向同性均勻右手材料中以入射角θ0=30°入射到含這種never cut-off非線性不定介質的一維光子晶體中，在這種情況下，可以得到負的雙穩(wěn)態(tài)GH位移。此時所得的結果與（ii）類似，但雙穩(wěn)態(tài)GH位移的峰值略小，僅為10.65個波長。透射光束相位φt在高閾值與低閾值處發(fā)生跳變。

當入射光強度從一個大于高閾值點處的值開始減小時，S隨之增大，當入射光強度減小到低閾值點時，S在此處達到正最大值。透射光束相位tφ的斜率在高閾值與低閾值處發(fā)生躍變，這恰恰說明了透射光束雙穩(wěn)態(tài)GH位移的合理性。

四、結論

本文利用傳輸矩陣法和穩(wěn)態(tài)相位理論，在五個不同的頻率范圍內研究了光束在含左手材料與Kerr非線性不定介質缺陷層一維光子晶體中的非線性傳播特性。研究表明當非線性不定介質缺陷層為cut-off和never cut-off介質時，透射光強與入射光強存在光學雙穩(wěn)態(tài)特性。。研究成果為制作高性能的光電探測及光開關器件提供了有益的參考。

[1]R.A.Shelby,D.R.Smith,and S.Schultz,Science 292,77(2001).

[2]V.G.Veselago,Sov.Phys.Usp.10,509(1968).

[3]D.R.Smith,W.J.Padilla,D.C.Vier,S.C.Nemat-Nasser,S. Schultz,Phys.Rev.Lett.84,4184(2000).

[4]F.Goos,H.H?nchen,Ann.Phys.1,333(1947).

[5]O.Emile,T.Galstyan,A.Le Floch,F.Bretenaker,Phys.Rev.Lett. 75,1511(1995).

[6]Y.S.Kivshar,Nature Physics 2,729(2006).

[7]P.Hou,Y.Y.Chen,X.Chen,J.L.Shi,Q.Wang,Phys.Rev.A 75,045802(2007).

[8]D.R.Smith,D.Schurig,Phys.Rev.Lett.90,077405(2003).

[9]N.H.Liu,S.Y.Zhu,H.Chen,X.Wu,Phys.Rev.E 65,046607 (2002).

[10]X.Chen,C.F.Li,Phys.Rev.E 69,066617(2004).

[11]S.Dutta Gupta,D.S.Ray,Phys.Rev.B 38,3628(1988).

[12]T.E.Hartman,J.Appl.Phys.33,3427(1962).

[13]R.Ruppin,Phys.Lett.A 277,61(2000).

[14]S.D.Gupta and G.S.Agarwal,J.Opt.Soc.Am.B 4,691(1987).

[15]R.Wang,J.Dong,D.Y.Xing,Phys.Rev.E 55,6301(1997).