有效設計探究活動

孫紅偉

摘要：新課程標準的課堂教學重點由注重學習結果轉向注重學習過程，這就給教師提出了新的要求，即教師的教學行為能給學生提供去體驗探究學習的過程和經歷的機會，最終有效促進學生教學知識的自主建構。探究性學習是一種積極的學習過程，學生以某個問題作為突破點，通過質疑、調查、分析、交流等活動，獲得知識，激發情趣，掌握方法。如何增強學生探究的自信心和求解問題的耐心，提高學生參與學習活動中主動進行決策的興趣、意識和能力，需要有效設計探究活動。

關鍵詞：體驗；探究；自主建構；興趣；意識；能力

中圖分類號：G623.5文獻標識碼：A 文章編號：1992-7711（2015）09-074-2

教學《多邊形的面積計算》這一單元的內容時，考慮到小學五年級學生已經具有一定的抽象思維能力，應鼓勵學生主動探求知識，激發學生學習的興趣和探究欲，給予學生充足的時間和廣闊的空間，并挖掘出教學內容中蘊含的豐富價值。

激發探究的欲望

探究是一種需要，探究欲實際上就是一種求知欲，它解決的是“想不想”探究的問題。課堂教學中，教師的一個十分重要的任務就是培養和激發學生的探究欲望，使其處于一種探究的沖動之中。

如教學《平行四邊形的面積》，課前為每位學生準備下面的一份材料。

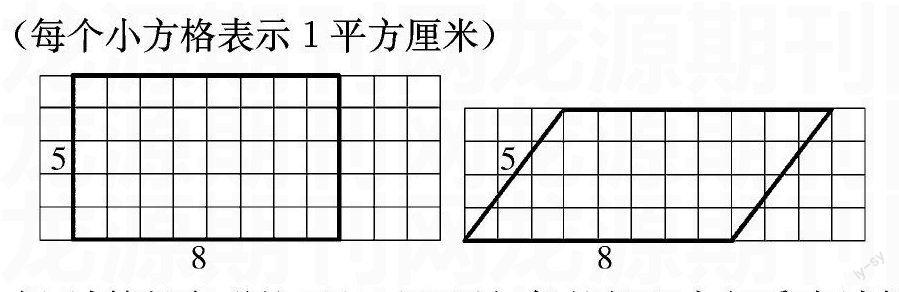
（每個小方格表示1平方厘米）

師：計算長方形的面積可以用相鄰的長和寬相乘來計算，計算平行四邊形的面積也可以用這種方法嗎？

生1：長方形的長和寬相交成直角，而平行四邊形相鄰的兩條邊相交成的不是直角。

生2：長方形的面積是8×5=40（平方厘米），如果平行四邊形也這樣計算，感覺平行四邊形的面積比長方形小了一點。

生3：如果我們把左邊的一塊三角形剪下來平移到右邊，正好能拼成一個長方形，長方形的長還是8厘米，只是寬變成了4厘米。

生4：4厘米其實是平行四邊形的高，平行四邊形的面積應該用底乘高來計算。

師：到底是8×5還是8×4？請利用手中的工具驗證自己的猜想。

很快，學生將探究的方向聚焦于平行四邊形轉化為長方形上，學生探究的欲望被激發了出來，剪、拼得十分熟練。對于不同意見，學生覺得有必要去探究；對于似曾相識的算式，學生覺得有方向去探究，探究的主動性和欲望不言而喻。

擴展探究的空間

長期以來，學生習慣于按照書上寫的與教師教的方式去思考問題，用符合常規的思路和方法解決問題，這對于基礎知識和基本技能的掌握是必要的，但對于數學興趣的激發，智力能力的發展，特別是創造性思維的發展，顯然是不夠的，課堂上應給予學生充足的時間和廣闊的空間，引導學生動手實踐、自主探索、合作交流。

如教學《三角形的面積》，教科書后面的三角形，筆者沒有布置學生剪下來，但要求他們帶剪刀來。

師：我們已經知道通過剪、拼將平行四邊形轉化成長方形，如何計算三角形的面積呢？

學生議論開了，有的說轉化成長方形，有的說轉化成平行四邊形。

生1：將直角三角形的兩條直角邊相乘，就是一個長方形的面積，除以2就得到直角三角形的面積，也就是直角三角形的面積等于底乘高然后除以2。

筆者繼續問道：“銳角三角形和鈍角三角形的面積也可以這樣計算嗎？”這個學生果然沒有讓筆者失望，他把課本投放到展臺上，繼續說道：“用三角形的底乘高得到長方形的面積，每個三角形的面積正好是長方形面積的一半。”

還有的學生想到了下面的方法：“將上面的三角形剪拼到下面，正好拼成一個長方形，長方形的長就是三角形的底，寬變成了高的一半，所以用底乘高除以2就是三角形的面積。”

筆者很驚訝，原來三角形和長方形有如此淵源。當然也有用兩個完全一樣的三角形拼成平行四邊形來推導的：“我是用兩個完全一樣的三角形拼成一個平行四邊形，平行四邊形的底就是三角形的底，平行四邊形的高就是三角形的高，每個三角形的面積是平行四邊形面積的一半，平行四邊形的面積是底乘高，三角形的面積就是底乘高除以2。”

通過這節課的探究，學生不僅掌握了三角形的面積計算方法，更增強了求異的意識，培養了學生的創造性。

挖掘探究的價值

數學教學是一種有計劃、有組織的創造性活動，在數學教學中，教師提供數學素材，幫助學生銜接已有知識和經驗，發展新的數學觀念，建構數學。教師要準確地把握每一節課的學習內容，設計出符合學生認知規律的問題，讓學生通過觀察猜想、實驗證明等活動尋求數學經驗，充分挖掘探究內容的價值。

如教學下面的問題：

小明參觀鋼鐵廠時看到許多鋼管堆成如下圖的形狀。最上層有9根，最下層有16根，有8層。

大部分學生用加法計算：9+10+11+12+13+14+15+16=100（根）。這種方法學生容易理解，但是寫起來比較繁瑣。于是筆者故意啟發學生：“瞧，它的橫截面是什么形狀的？”很快有學生想到了計算方法：（9+16）×8÷2=100（根）。

筆者反問學生：“怎么計算鋼管的根數變成了計算橫截面的面積了？”學生一臉茫然，這時，一名女生站起來說道：“如果找同樣多的一堆鋼管，倒過來與它拼起來，橫截面就成了平行四邊形。這樣每層都有9+16=16（根），一共8層，所以每堆鋼管就有（9+16）×8÷2=100（根）。”

筆者表揚了這位同學。這位學生又很快發現：“梯形的上底就是第一個加數，下底就是最后一個加數，高就是加數的個數。”接著我又出示了兩個加法算式，要求學生用梯形面積公式計算。

9+10+11+12+13+14+15+16+17+18

1+2+3+4+5+……+15+16+17+18

其中一位學生站起來激動地說道：“我早就知道連續的自然數相加，可以用第一個數與最后一個數的和乘以自然數的個數，再除以2這種方法計算。”

這樣的教學內容，加強了數學與生活的應用聯系，提高了學生解決問題的能力，同時為以后的學習做好了鋪墊。