幾何畫板融入中職數學教學的實踐與思考

葉素慧

【摘 要】《中等職業學校數學教學大綱》要求教師更新觀念、優化傳統的教學方法，充分發揮計算機、互聯網等現代信息技術的優勢。在“重視現代信息技術與課程的整合，努力推進現代信息技術在職業教育教學中合理的應用”的道路上，信息技術與數學教學的整合已有了許多有益的嘗試和研究。本文從幾何畫板在中職數學教學中的實例著手，剖析幾何畫板與中職數學教學的整合，使學生好學、會學、學會、學好。

【關鍵詞】幾何畫板；中職數學； 整合

【中圖分類號】G712 【文獻標識碼】B

【論文編號】1671-7384（2015）06-0078-03

幾何畫板融入中職數學教學的必要性

1.符合大綱理念和教學新要求的需要

《中等職業學校數學教學大綱》要求教師更新觀念、優化傳統的教學方法，充分發揮計算機、互聯網等現代信息技術的優勢。所以適當引入信息技術，加強其在教學中的地位，有利于學生理解數學概念、擴展思路，主動探索。

2.中職生現狀的需要

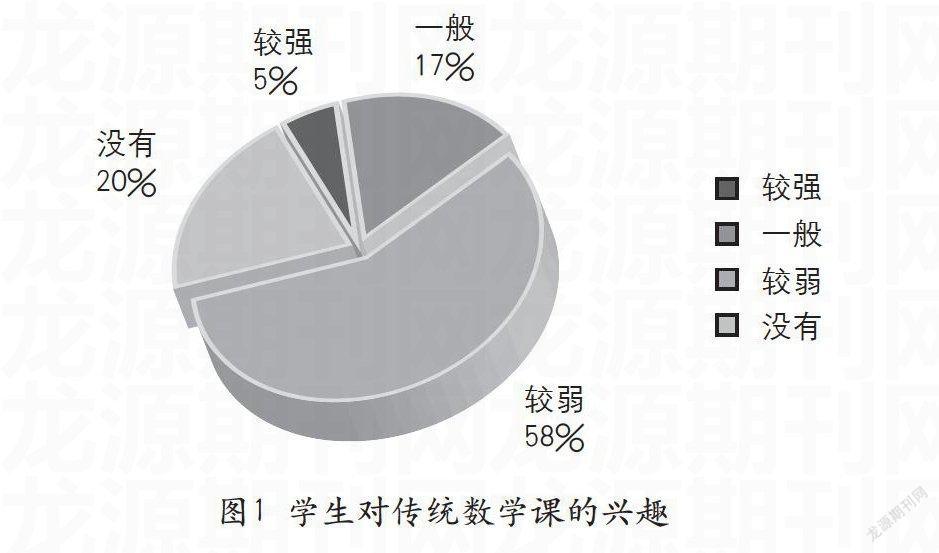
目前，中職數學教學面臨許多困惑與挑戰，部分學生起點低、差異大、極度厭學，尤其是數學學科，“老師幾乎在課堂上唱獨角戲”已成為中職數學課堂教學正常開展的瓶頸。如何激發學生學習興趣，讓學生參與課堂，是每位教師都在思考的問題。幾何畫板既能創設情境又能讓學生主動參與，能有效地激發學生的學習興趣，使抽象、枯燥的數學概念變得直觀、形象，使學生從害怕、厭惡數學變成喜愛數學并樂意學習數學。學生通過主動發現、主動探索，不僅使其邏輯思維能力、空間想象能力和數學運算能力得到訓練，而且還能有效培養其發散思維和直覺思維。筆者對本校的720名學生做了調查，結果顯示，學生對數學的學習態度不樂觀，而對與信息技術整合的數學課感興趣 。

如圖1所示，近80%的學生對學習數學的興趣是一般和較弱，只有5%的學生有較強的興趣，20%的學生沒有興趣。從這些數據上看出，數學教師的任務非常艱巨，改變課堂教學模式、提高學生學習興趣是當務之急。

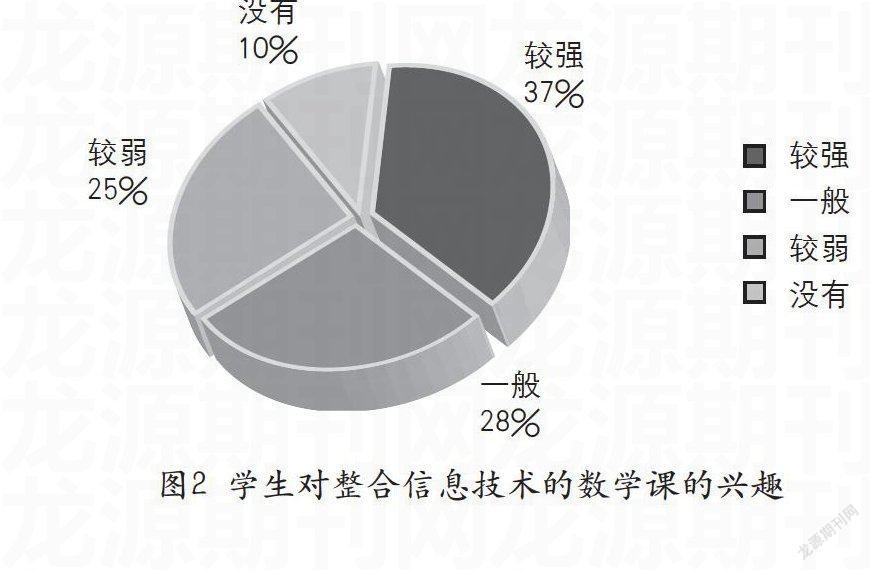
如圖2所示，65%的學生對整合信息技術的數學課有興趣，因為動畫不僅吸引眼球，而且形象直觀。幾何畫板融入數學課中，能有效地激發學生的學習興趣。

幾何畫板有效融入中職數學教學的嘗試

1.利用《幾何畫板》搭建突破概念教學難點的平臺

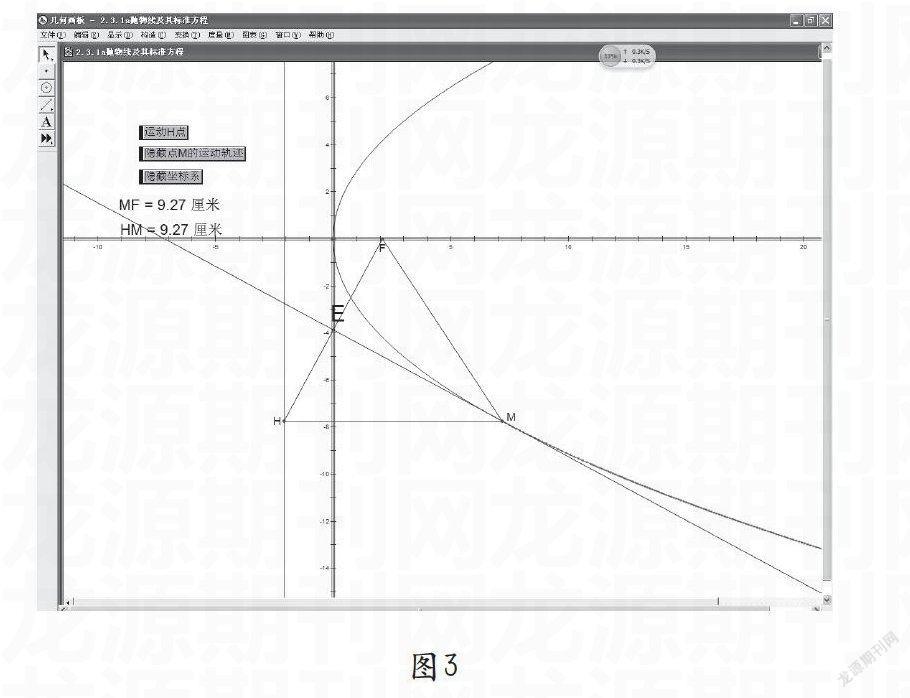
【案例一】問題：平面內動點M滿足到定點F與到定直線l的距離相等，動點M的軌跡是什么？

傳統教學的不足：（1）若用尺規作圖，涉及的一個距離是點到直線的距離，需要作垂線，找到垂足，再用直尺測量，不易操作。（2）找到的點個數有限，不能形成連續曲線，不易通過觀察得到結果。

利用幾何畫板解決：（1）畫出一條直線l和一個定點F，且點F不在直線l上。（2）在直線l上取點H，過點H作L的垂線MH。（3）作線段HF的中垂線，交MH于M。 （4）取M，并追蹤點M的運動軌跡。（5）在直線l上拖動點H運動（或生成點H的動畫，讓其沿直線反復運動），則形成點M的運動軌跡——拋物線，如圖3所示。

技術支持：（1）隨著對某個幾何對象的拖動，已構建的幾何關系仍保持有效，幾何圖形變成動態的。同時，通過動畫功能可以自動完成拖動幾何圖形的工作，從而生成美觀、有趣且有啟發性的圖形，并且它們都是動態的，幾何畫板就是一個動態的幾何學環境。（2）幾何畫板能由較簡單的動畫和運動通過定義、構造和變換，得到所需的復雜運動。使用便捷的軌跡跟蹤功能，能清晰地了解目標的運動軌跡。橢圓和雙曲線的形成可以通過實物模擬，但拋物線的實物模擬并不容易想到，且不易實現，利用幾何畫板的動態功能和追蹤功能，解決了很多教師無法呈現拋物線形成過程的煩惱。

2.利用《幾何畫板》搭建驗證問題和揭示問題本質的技術平臺

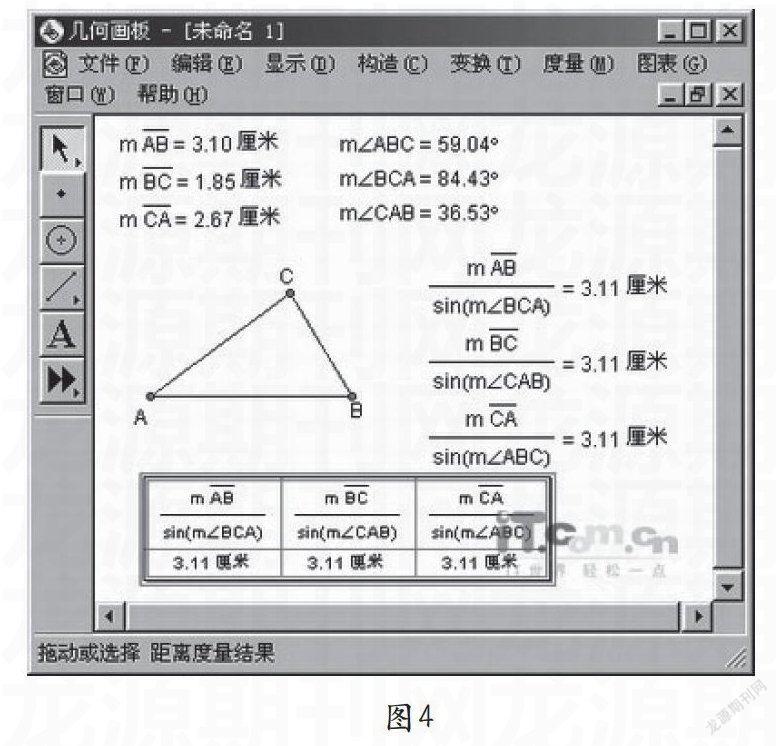
【案例二】：問題：在Rt△中，邊與角之間是否存在等量關系：，是不是在一般三角形中也存在這樣的邊角關系？如何檢驗結論是否成立？

傳統教學的不足：（1）通常教師讓學生在直角三角形中證明這一性質，而在斜三角形中要證明對中職學生比較難，往往就草草地說明也適用。（2）如果通過實驗指導學生畫出任意一個三角形，需要用直尺和量角器對三條邊和三個內角進行測量，測量數據有一定誤差；角度一般都不是特殊角，需要查表或用計算器計算其正弦值，再代入運算，運算結果也會存在誤差。

如圖4所示，利用幾何畫板解決： （1）畫出三個不共線的點，并用線段把它們連接起來，形成三角形ABC。（2）度量三個內角的大小及三條邊的長度。（3）計算三個比值：，，。（4）拖動頂點A，可以任意改變三角形的形狀，從而引起三個內角及三條邊的數值變化，可以觀察到三組比值雖然在變，但總保持相等。

技術支持：（1）幾何畫板最大的特色就是“動態性”，即可以用鼠標拖動圖形上的任一元素（如點、線、圓等），而事先給定的所有幾何關系（即圖形的基本性質）都保持不變。在上述三角形中，我們拉動其中的一個點，同時圖形的形狀就會發生變化，但仍然保持是三角形。（2）幾何畫板具有強大的計算功能，不僅能完成定值的計算，還能進行變量的計算。教師選擇用幾何畫板完成檢驗過程，不僅省去了煩瑣的度量計算，還讓學生直觀感受到結論的正確性。

3.運用幾何畫板為揭示變化規律創建平臺

【案例三】：探索正弦型函數y=sin（wx+j）的函數圖象性質。

傳統教學的不足：一般課程中都是以三個特殊值來說明，幾個有限的取值描述后就加以歸納，其不全面的歸納對學生的認知影響是顯而易見的。

利用幾何畫板解決：拖動課件中的A，w，j，就可以在其下面看到相應的值（如圖5），同時可以看到函數圖象的連續變化，通過直觀生動的圖象變換，學生很容易就能完成y=Asin（wx+j）的函數性質的學習。

技術支持：（1）隨著對某個幾何對象的拖動，幾何圖形變成動態的。同時，通過動畫功能可以自動完成拖動幾何圖形的工作，從而生成美觀的或有趣的或很有啟發性的圖形，并且它們都是動態的。（2）幾何畫板不僅省去了畫圖的時間，讓學生直觀感受圖形變化規律，還使教學過程形象生動，大大提高了課堂效率，激發了學生學習的興趣。

幾何畫板融入中職數學教學的思考

1.運用幾何畫板要科學合理

新技術是一把雙刃劍，使用不當自然會有一定的副作用。一線教師使用幾何畫板輔助數學教學時應通盤考慮幾何畫板的性能特征、學生學習心理和思維規律、具體授課內容等，遵循實事求是、主體參與的原則。幾何畫板輔助教學和傳統教法各有利弊，不是“非此即彼、完全取代”的關系，而應有機結合，互為補充，該用傳統教法的課，不必作繭自縛而舍近求遠。另外，數學教師不應坐失良機，更不應該排斥看似簡單的幾何畫板或盲目崇拜新技術。

2.運用幾何畫板要適時適量

符合學生的認知規律運用幾何畫板教學，可減少教師的講解，且助于教師的講解。教師的講解要與演示緊密結合，不論采用何種方式講解，都應抓住教學內容的重點、難點、要點、疑點，抓住教學內容的內在聯系進行講解。在使用課件之前，應告訴學生觀察什么，使學生有明確的目標，以便集中精力先看什么后看什么。怎樣演示（如先拖動還是先動畫），是否重復演示都要十分講究，要縝密考慮，做到胸有成竹。

3.運用幾何畫板實現數學課堂組織形式的開放

如果有條件的話，可以把課堂從多媒體教室轉移到微機教室，讓每位學生都親自動手實驗，改變任何一個參數，通過觀察、比較、分析得出自己的結論，這樣的效果更理想。學生在互相討論、教師點撥指導等過程中，得出自己的結論，逐漸形成自己的知識體系，達到知識的重建，這有利于學生從實踐中發現問題、解決問題，主動地學習數學，提高數學思維能力。通過此方法，教師可以把學生從被動的學習中解脫出來，主動地思考數學問題，真正提高學生的學習能力。這種開放性的教學可以培養和促進學生的好奇心和求知欲，激發學生探索的熱情。

總之，應用幾何畫板進行中職數學教學，能使中職學生更有實感地去把握數學，而不是把數學作為單純的知識去理解，既能激發中職學生的學習熱情、培養中職學生學習數學的興趣，又能大大提高課堂效率。

（作者單位：浙江臺州市椒江中等職業技術學校）