一道浙江競賽題引發的思考

沈小紅 計惠方 (湖州市王勇強名師工作室 浙江湖州 313000)

?

一道浙江競賽題引發的思考

沈小紅 計惠方 (湖州市王勇強名師工作室 浙江湖州 313000)

2015年浙江省高中數學競賽中有這樣一道形式優美，入口平寬，解法眾多，創意新穎,內涵豐富的好試題.

1)求橢圓C1的方程；

2)若直線l與曲線C1，C2都只有一個公共點，記直線l與圓C2的公共點為A，求點A的坐標．

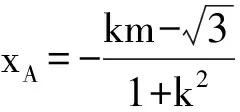
消去y得 (1+4k2)x2+8kmx+4m2-4=0,

從而

Δ1=16(4k2-m2+1)=0,

即 4k2-m2+1=0.

(1)

聯立方程組

消去y得

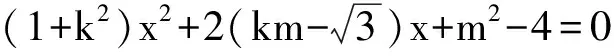
從而

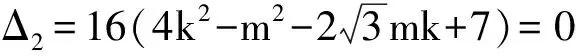
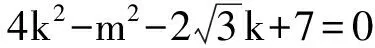
(2)

經檢驗A(0,2)或A(0,-2)符合題意，故所求點A的坐標為(0,2),(0,-2).

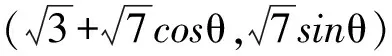
聯立方程組

消去y得

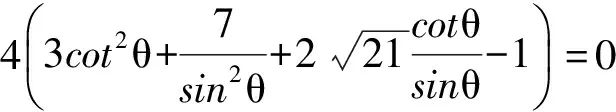
令Δ=0解得

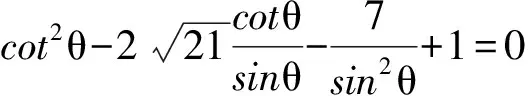
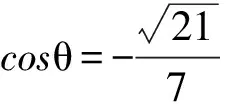
經檢驗A(0,2),或A(0,-2)符合題意，故所求點A的坐標為(0,2),(0,-2).

1 賽題的另解

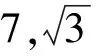
圖1

經檢驗A(0,2)或A(0,-2)符合題意，故所求點A的坐標為(0,2),(0,-2).

2 賽題的推廣

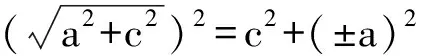
消去y得

(b2+a2e2)x2+2a3ex+a4-a2b2=0，

即

x2+2cx+c2=0,

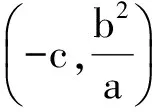
證明 當公切線l的斜率不存在時，顯然不滿足題意.當公切線l的斜率存在時，可設直線l的方程為

y=mx+n(其中m,n∈R)，

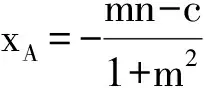
消去y得

(a2m2+b2)x2+2a2mnx+a2n2-a2b2=0,

(3)

從而

Δ1=4(a2m2-n2+b2)=0,

即a2m2-n2+b2=0.

(4)

消去y得

(1+m2)x2+2(mn-c)x+n2-a2=0，

從而

Δ2=4(a2m2+a2-2mnc+c2-n2)=0,

即a2m2+a2-2mnc+c2-n2=0.

(5)

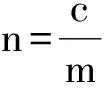
a2m4+b2m2-c2=0，

即

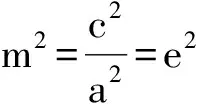
故

因此曲線C1,C2的公切線有且僅有2條，其方程分別為

l1:y=ex+a和l2:y=-ex-a.

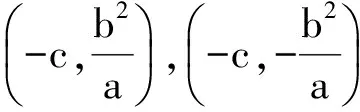
3 賽題的引申

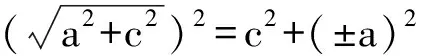
消去y得

(b2-a2e2)x2-2a3ex-a4-a2b2=0，

即

x2+2cx+c2=0,

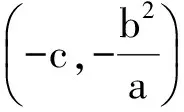
證明同命題1′(略).

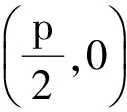
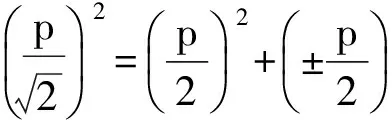
消去y得

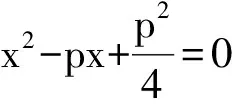
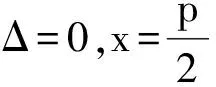
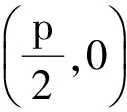
證明同命題1′(略).