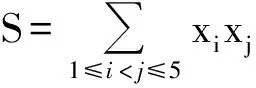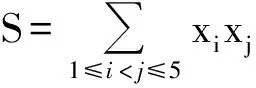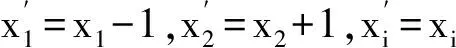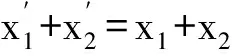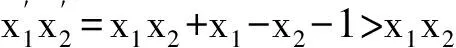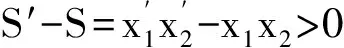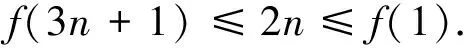例談數學競賽中的局部調整法
盧學謙 (泰安市第一中學 山東泰安 271000) ●盧 健 (萊城區羊里中學 山東萊蕪 271118)
?
例談數學競賽中的局部調整法
盧學謙 (泰安市第一中學 山東泰安 271000) ●盧 健 (萊城區羊里中學 山東萊蕪 271118)
局部調整法也稱為逐步調整法,就是暫時固定問題中的一些可變因素,研究另一些可變量對求解問題的影響,取得局部成果后,再設法求得整個問題的結果.例如著名的算術-幾何平均值不等式的證明,2014年“北約”自主招生考試數學試題第10題以及2014年全國高中數學聯賽加試第4題都可用局部調整法.先來看一道經典競賽題:
1 趣味調整,進入境界
例1 已知銳角△ABC中,∠A>∠B>∠C.在△ABC的內部(包括邊界上)找一點P,使得點P到3條邊的距離之和最小.
分析 這是一道趣味競賽題.我們先考慮特殊情況,當點P在△ABC邊界上的什么位置時,點P到3條邊的距離之和最小,然后再對點P在△ABC的內部時進行研究.
解 1)先研究點P在△ABC的邊界上時的情況:
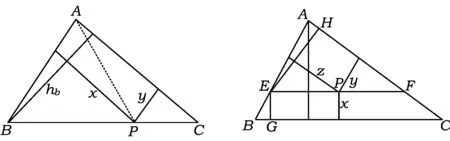
①若點P在邊BC上.如圖1,記△ABC的頂點A,B,C對應的邊分別是a,b,c,邊a,b,c上的高分別為ha,hb,hc,點P到邊c,b的距離分別為x,y,聯結PA.因為∠A>∠B>∠C,所以ha 因此hb≤x+y(當x=0時,取到等號),即點P在點B處時,點P到3條邊的距離之和最小. ②若點P在邊AC上,點P在點A處時,點P到3條邊的距離之和最小. ③若點P在邊AB上,點P在點A處時,點P到3條邊的距離之和最小. 綜合①,②,③,當點P在點A處時,點P到3條邊的距離之和最小. 圖1 圖2 2)再研究點P在△ABC內部時的情況:如圖2,過點P作BC的平行線交AB于點E,交AC于點F,固定x,由第1)小題知, x+y+z>EG+EH. 讓x變化,得 EG+EH≥ha, 從而 x+y+z>ha. 綜合1),2)知,當點P在點A處時,x+y+z最小. 注 本題先對點P在邊界上進行調整,獲得問題的局部解決.經過若干次這樣的局部調整,逐步逼近目標,最終得到問題的整體解決. 例2 已知x1,x2,…,xn∈R+,且x1x2…xn=1,求證: (2014年“北約”自主招生考試數學試題第10題) 分析 本題解法很多,但利用調整法最為簡便. 證明 1)若x1=x2=…=xn=1,待證式等號成立. 所以f(x1,x2,…,xn)>f(1,x1x2,x3,…,xn).這說明把(x1,x2)調整成(1,x1x2)后,f(x1,x2,…,xn)的值變小,依此類推,每調整一次,f(x1,x2,…,xn)的值減少一次,這樣,最多經過n-1次調整,(x1,x2,…,xn)變成(1,1,…,1),從而 f(x1,x2,…,xn)>f(1,x1x2,x3,…,xn)> f(1,1,x1x2x3,…,xn)> 綜上所述,原不等式成立. (1) 于是 (1-x1)(1-x2)…(1-xn)≥ (1-x1) (1-x2)…(1-xn)≥ 注 本題把變量的取值向左、右2個方向調整,直至最大量的值是1,其余量都是0,與例1稍有區別,代表了局部調整法證明不等式的2種風格. 例4n(其中n≥4)個盤子里放有總數不少于4的糖塊,從任意選出的2個盤子里各取1塊糖放入另一個盤子中稱為一次操作,問能否經過有限次操作,把所有的糖塊集中到1個盤子里去?證明你的結論. (第9屆CMO試題) 分析 經過嘗試,可經過有限步操作使所有糖塊集中到2個或3個盤子里,這就為進一步探索打開了缺口. 解 首先證明可經過有限步操作使所有糖塊集中到2個或3個盤子里. 事實上,如果放糖的盤子不少于3個,任取其中3個盤子,分別記為A,B,C,并設A,B,C中分別有a,b,c(其中0 (a,b,c) →(a-1,b-1,c+2)→… →(0,b-a,c+2a). 即放有糖塊的盤子的總數減少1個(當a≠b時)或2個(當a=b時),這樣繼續下去,總可以將糖塊集中在2個或3個盤子中. 其次,不妨設所有糖塊集中在盤子A,B,C中,每個盤中放的糖塊分別為a,b,c(其中a≥b≥c≥0).另取一個空盤D(由n≥4,知至少有4個盤子),上述狀態簡記為(a,b,c,0).如果a,b,c中有2個相等,那么上述證明可經過有限步將糖塊集中到1個盤子中,故只要考慮a>b>c≥0的情形,又分為下列2種情形: 2)若a>c+2,則先作如下操作: (a,b,c)→(a-1,b-1,c+2), 因為a>b>c及a>c+2,所以 a-1>b-1≥c,a-1≥(c+3)-1=c+2, 故經過調整后,3個盤子中所放糖塊量的最大數減少1,而最小數不減少,故經過有限調整可歸結為有2盤糖塊數相等或情形1),于是由前面證明可知經過有限步操作可將糖塊集中到1個盤子中. 但在有些問題的解決過程中,變量的流向并不明顯,需輔以直覺作出判斷. 1)當x1,x2,x3,x4,x5取何值時,S取到最大值? 2)進一步地,對任意1≤i≤j≤5有|xi-xj|≤2,當x1,x2,x3,x4,x5取何值時,S取到最小值?說明理由. (2006年全國高中數學聯賽試題) |xi-xj|≤1(其中1≤i≤5,1≤j≤5). (2) 將S改寫成 x1x2+(x1+x2)(x3+x4+x5)+x3x4+ x3x5+x4x5, 同時有 x3x5+x4x5, 于是 這與S在x1,x2,x3,x4,x5時取到最大值矛盾.因此 |xi-xj|≤1(其中1≤i≤5,1≤j≤5). 當x1=402,x2=x3=x4=x5=401時取到最大值. 2)當x1+x2+x3+x4+x5=2 006且|xi-xj|≤2時,只有如下3種情形滿足要求: ①402,402,402,400,400; ②402,402,401,401,400; ③402,401,401,401,401. 例6S是由在同一條直線上個點構成的一個集合,隨機地選擇其中的4n個點染成藍色,其余2n個點染成綠色.證明:存在一條線段,使其包含S中的3n個點,其中2n個點為藍色,n個點為綠色. (2008年巴西數學奧林匹克競賽試題) (3) 再考慮當i=1,2,…,3n時,f(i+1)與f(i)的關系: 若Ai,Ai+3n同色,則 f(i+1)=f(i); 若Ai為藍色,Ai+3n為綠色,則 f(i+1)=f(i)-1; 若Ai為綠色,Ai+3n為藍色,則 f(i+1)=f(i)+1. 總之,|f(i+1)-f(i)|≤1,結合式(3)知必存在j∈{1,2,…,3n+1}使f(j)=2n,即存在一條線段恰好包含S中Aj,Aj+1,…,Aj+3n-1這3n個點,其中2n個點為藍色,n個點為綠色. 注 本例把包含前3n個點的線段看作原始狀態,每步調整時去掉最前面那個點并添加后面相鄰的一個點.調整過程中可證明存在一個時刻,連續3n個點中恰有2n個藍色點. 由以上例題可以看出,局部調整法的精髓可以體現在以下4個方面: 1)通過調整,使原狀態達到某種意義下更優的狀態,從而逐步達到最優狀態(注意必須以最優狀態存在為前提); 2)通過調整,將大量一般的情形歸結為討論少數幾類特殊的、規則的情形,使問題便于解決; 3)在按某種條件或要求進行操作時,掌握操作過程中的某種內在規律(如不變性、奇偶性、同余性、連續性、單調性等)進行逐步調整,使之得出某種結論; 4)為尋找某種對象,在滿足部分限制條件的前提下,通過調整使其余限制條件也得以滿足. [1] 張小明.例談局部調整法在不等式證明中的應用[J].中學教研(數學),2014(9):37-38. [2] 鄭日鋒.數學競賽中的局部調整策略[J].中等數學,2004(4):10-11. [3] 蘇勇,熊斌.不等式的解題方法與技巧[M].上海:華東師范大學出版社,2013:119-120. [4] 盧學謙.數學教學中對學生思維深刻性的培養[J].中學數學雜志,2014(11):23-25.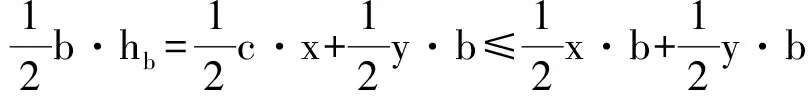
2 逐次調整,妙不可言
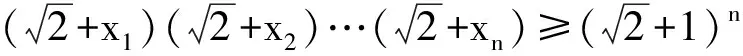
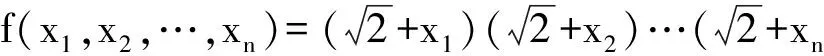
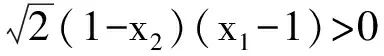
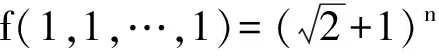
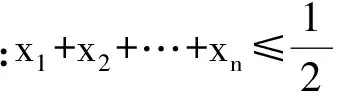

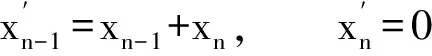

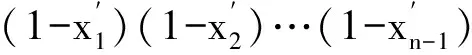
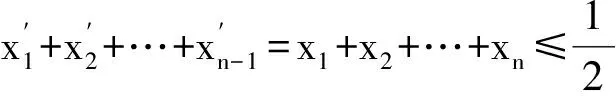
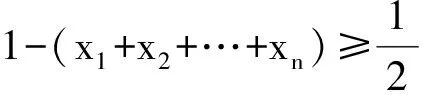
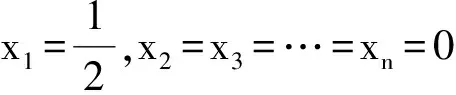
3 嘗試調整,觸類旁通
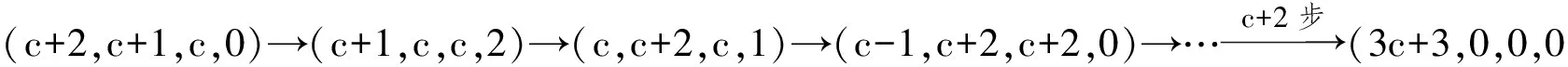
4 直覺調整,茅塞頓開