結構觀在規則課教學中的應用研究
——以“余弦定理”第一課時教學為例

●沈 良 (蕭山區第五高級中學 浙江杭州 311202)

結構觀在規則課教學中的應用研究
——以“余弦定理”第一課時教學為例

●沈 良 (蕭山區第五高級中學 浙江杭州 311202)

數學學習按知識分類有概念學習、規則學習和問題解決學習，相應的課堂教學有概念教學、規則教學和問題解決教學.一般地，數學規則學習包含數學公理、定理、法則、公式等內容的學習.數學規則是幾個數學概念之間關系的陳述，其表現形式是語言和符號，這些語言和符號是數學家們根據對客觀事物屬性的感知進行思維構造的結果.因此數學規則以數學概念為基礎，反映若干概念之間的關系;同時，數學規則以問題解決為目的，反映在數學規則的應用方面.可以說數學規則是聯結數學概念與數學問題解決的橋梁，是數學問題解決的重要工具.

數學規則表現為一定的語言和符號，總是包含某種特定內容，諸如一定的背景、意義與功能等;數學規則總是呈現某種特定形式，表現為一定的結構特征;數學規則總是蘊涵某種特定思維，給予學生思考落腳點.文獻［1］指出:結構觀下的教學應凸顯結構的地位，使學生的學習、解題、反思等活動都能適度地從結構的形式、特征與功能等角度出發思考.因此在規則教學中，如何在規則的引入、證明、特征探索及應用中融入結構觀，啟迪學生思維，值得我們研究.筆者結合“余弦定理”第1課時的教學，談談“結構觀”在規則教學中的融入.

1 感知識別，鋪墊規則

“感知識別，鋪墊規則”指設置恰當的問題情景，激發學生思考，初步感知與識別問題，為新規則的學習作好鋪墊.設置恰當的問題，當以學生的最近發展區為出發點，利用靈活多變的教學方式，激發學生的學習熱情.如由特殊到一般的方式實現規則的猜想，由具體到抽象的方式實現規則的歸納，由其他事物的性質實現規則的類比，由開放性的問題實現規則的尋根究底，等等.

實錄1 呼喚新工具——余弦定理的引入

師:前面我們學習了正弦定理，請思考正弦定理能夠幫助我們解決什么樣的解三角形問題?

生1:“2角1邊”和“2邊1角”問題.

師:在“2角1邊”中，邊是對邊還是鄰邊?

生1:好像對邊和鄰邊都可以.如果知道∠A，∠B和邊長a，利用正弦定理，就能求邊長b，∠C和邊長c;如果知道∠A，∠B和邊長c，可以先求得∠C，再去求邊長a和b.

(教師結合正弦定理同步展示).

師:那在“2邊1角”問題中，角是對角還是夾角?

生1:若是對角，比如知道邊長a，b和∠A，由正弦定理可先求∠B，再求∠C和邊長c.若是夾角，如果知道邊長a，b和∠C，用正弦定理似乎解不了.

師:針對“2邊1夾角”問題，正弦定理似乎無能為力，但已知“2邊1夾角”的三角形確定嗎?為什么?

生2:確定，因為根據初中知識“邊角邊”對應相等可以判斷三角形全等.

師:嗯，既然確定，那么我們能否來解這個三角形呢?不妨先思考下列問題:在△ABC中，已知邊長a，b和∠C，試求邊長c.

……

評析 通過“正弦定理能解決什么樣的解三角形問題”，復習舊知，有效幫助學生梳理解三角形的幾個問題，并由學生所提“2角1邊”、“2邊1角”問題細化為“2角1對邊”、“2角1鄰邊”、“2邊1對角”和“2邊1夾角”問題.又為引入新知作好鋪墊，尋求“2邊1夾角”問題的解決.這里的結構一方面表現為“幾何圖式”，根據三角形中已知的一些邊角元素進行歸類劃分;另一方面表現為“方程形式”，運用“知三求一”或“知二求二”思想剖析解決.

2 推導固化，建構規則

“推導固化，建構規則”是指以問題情景或猜想結論等為背景，通過適當的教學方法，引導學生應用已有知識方法推導與建構規則.這是“感知識別”基礎上的發展過程，是培養學生探究能力的過程，也是進一步啟發學生思維的過程，亦是充分挖掘規則建立中蘊含思想方法與思維價值的過程.

實錄2 尋找新方法——余弦定理的推導

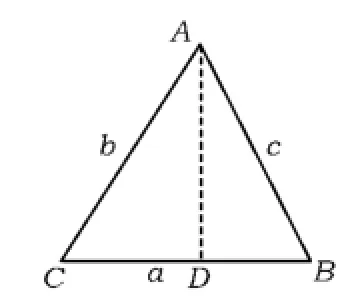
圖1

余弦定理推導過程中，拋出問題“在△ABC中，已知邊長a，b和∠C，試求邊長c”，給予學生足夠時間探究，主張由學生發現定理證明的各種方法.當然，限于學生的知識與能力水平，探究不能一蹴而就，此時教師的引導非常重要，“憤”、“悱”狀態下學生的思維是最活躍的，加上教師畫龍點睛，學生會思如泉涌.

生3:過點A作AD⊥BC于點D，則

AB2=AD2+DB2=(AC·sin C)2+(CB－CD)2，即

c2=b2·sin2C+(a－b cos C)2=

a2+b2－2ab cos C.

師:你是如何想到作高的?

生3:我想用勾股定理，因此作高試試看.

師:非常好，該同學將非直角三角形轉化為直角三角形.請大家思考這樣一個問題:三角形高線一定在三角形內部嗎?若高線在外部，結論是否還相同?

通過教師啟發，學生及時想到“當∠C為鈍角時，高線AD在三角形外部”的情形，同時發現結論不變.但當教師提問“其他同學是否還有其他證法”時，學生沉默不語，沒能聯想到向量法或坐標法等，思維的跳躍性似乎不夠，因此需要教師進行有效引導.

師:前面我們學習了向量，其中一節內容是向量在平面幾何中的應用，也就是說幾何問題能夠轉化為向量問題解決.“已知2邊及其夾角，求對邊長”，也就是求，如何解決?

所以 c2=a2+b2－2ab cos C.

師:你是如何想到的?

師:運用向量轉化和平方的技巧，能簡潔明快地求得長度c.事實上，余弦定理蘊涵于向量數量積定義之中，由“ ”可以直接構造出余弦定理，請同學們思考.

生6:用配方進行構造:

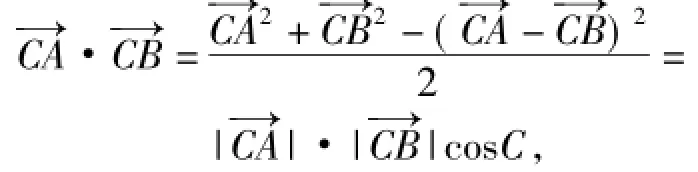
可得上述結論.

師:結合轉化思想，運用數量積定義可以巧妙構造出余弦定理，這也顯示了向量應用的普適性與數學知識的整體性.

師:要求邊AB的長，能否換個角度，AB的長也就是點A，B間的距離，你能聯想到什么?

生7:可以建立坐標系.

師:若是建系，你會建立怎樣的直角坐標系，點的坐標又會是多少?

生7:可以取點C為原點、CB為x軸、垂直于CB的直線為y軸.這樣B(a，0)，A(b cos C，b sin C)，從而AB的長度可求.

……

評析 對于方法1，作高是學生最能想到的，因為正弦定理證明中已有相關經驗，給予學生一定的探究時間，或多或少會有些收獲.而方法2、方法3的關鍵是如何幫助學生迅速聯想到方法，建立知識聯系.在宏觀上，要教給學生問題解決的方法，諸如高中平面幾何可用幾何法、向量法、坐標法(解析法)等解決問題，使學生在宏觀層面上有思考的視角.在微觀上，要培養學生的分析能力，特別是立足問題的結構形式與具體特征，展開分析聯想，如非直角結構化為直角結構，由“2邊1夾角”聯想到向量數量積，把長度視作2個點間的距離以及聯想到坐標法等，從而使思維有支撐點.

3 把握特征，賞析規則

“把握特征，賞析規則”是指規則建立之后，讓學生感知結構的特征形式，從而更好地利用規則解決問題.同時數學是美的，數學中的規則往往蘊含簡潔美、對稱美、符號美、理性美等，故教師要引導學生賞析結構中的各種美，激發學生喜愛數學的熱情.

實錄3 品味新規則——余弦定理賞析

余弦定理及其推論得到之后，教師不急于應用定理解決問題，而是先讓學生觀察余弦定理及其推論的結構形式.

生8:我覺得推論是一個二次齊次式，和我們學三角函數中的一類問題差不多.

師:這是怎樣的一類二次齊次式問題?

生8:如分子、分母中關于sin x，cos x都為二次的分式問題.

生9:我覺得余弦定理的3個式子呈相互輪換的形式.a2用 b2，c2與 cos A表示;b2用 c2，a2與cos B表示;c2用a2，b2與cos C表示，依次輪換，容易記憶.

……

評析 數學規則具有較強的抽象性、簡潔性與深刻性，學生接受一個新規則總需要一定的時間和過程.接觸到新規則之后，首要任務便是讓學生感受規則的特征形式與內涵，由外在形式去認識規則的內涵，加強對公式的感知與識別.

4 建立模式，應用規則

“建立模式，應用規則”是指應用規則，解決相應問題.數學中的規則往往具有廣泛的應用價值，能幫助我們解決一些相關問題.新課教學中，運用規則解決相關問題也是培養學生識別問題、建立模式的過程.特別是規則的應用之初，掌握一定的程式是十分有必要的，這也是培養學生掌握基本技能的過程.

實錄4 應用新規則——余弦定理的應用

例1 在△ABC中，已知b=3，c=1，A=60°，求邊長a.

練習1 在△ABC中，若a2+b2+ab－c2=0，則∠C =.

練習2 在△ABC中，b·cos C+c·cos B= ___________.

?練習3 在△ABC中，若AB=6，AC =3?且12，則BC =____________.

評析 例1～例3讓學生先獨立思考，再探討解決.因為是新課教學，難度設置較低，旨在讓學生初步學會運用余弦定理解決問題.其意義又是深刻的，3個問題包含3種情形，并讓學生總結思考“利用余弦定理可以解決哪些解三角形問題”，從而使學生體會到余弦定理應用的問題結構，如“2邊1角”和“3邊長”問題，而對于“2邊1對角”要視具體問題選擇正弦或余弦定理解決.

練習1設置的目的在于進一步應用結構特征解決問題，可以將條件構造成

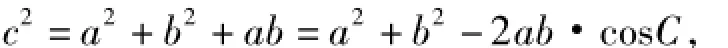
從而求得cos C;也可將等式轉化為

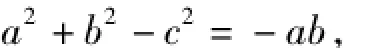
代入定理求解;2種方法都很好地利用了結構的特征形式.練習2的設置不僅在于利用余弦定理化簡等式，更在于培養學生的數形結合思想，培養學生運用幾何的方法看待數式意義.練習3既可以借助=12先求得cos A，再利用余弦定理求得BC;也可以化為，然后2邊平方求得BC，再次闡釋余弦定理與向量法緊密相連.

5 幾點反思

5.1 啟發思維

規則表現為一定的結構，結構蘊含一定的特征，特征能被學生感知、發現、聯想、轉化等，從而激活學生的思維.如上，余弦定理的發現、推導、證明與應用過程中，都展現了“結構”對學生思維的啟迪作用.余弦定理引入中，是對解三角形中特定幾何條件展開研究;余弦定理推導中，是立足特定的“長度”與“角度”展開聯想與方法探索;余弦定理應用中，是不斷嘗試并初步建立模式與識別.規則教學中，利用結構啟發學生思維應貫穿于規則的探索、建構與應用等一系列過程中.教師需利用屬性顯然的結構引導學生思考，點燃學生的思維，借助結構實現規則的識別、轉化、建構等.

5.2 實現探究

在數學中，規則總是包含豐富內涵，教師應創設條件給予學生足夠多的時間探究規則.1)規則形成階段:可以通過學生考察命題特例，然后抽象、概括出規則，也可以巧設問題情境，激發學生的求知欲;2)規則證明階段:要引導學生反思探究，從多種途徑、多種角度證明規則，有利于加深對數學規則的理解和記憶，有助于學生在不同的情境中運用數學規則解決問題，也有利于學生構建數學規則網絡;3)規則應用階段:不妨拋出問題讓學生展開思考，嘗試問題解決，通過自主探究、小組合作等方式，發現規則的應用模式，培養良好的探究能力.

5.3 內化結構

結構是外在形式和內在本質的統一體，外在形式或許通過記憶就能區分聯系，但對于內在本質的掌握就要求學生必須內化.在規則內化階段，需要明確數學規則的前提、結論和證明過程，明確規則前提的各部分對規則結論的影響，明確在何條件下適宜運用這一規則來解決問題;需要明確新學習的數學規則與已建立的數學規則網絡中的原有的數學規則之間的關系，明確它們之間的區別和聯系，并使新規則融合到相應的規則網絡和認知結構中去.只有當學生真正深刻理解這一系列問題時，才能做到“心中既有結構、心中又無結構”，真正實現結構觀下的解題與學習.

［1］ 沈良.略談數學結構觀下的解題與教學［J］.數學通訊，2012(12):1-3.