合 理 過 渡 自 然 生 成
——“對數的概念”之教學設計與思考

●崔志榮 (安豐中學 江蘇東臺 224221)

合 理 過 渡 自 然 生 成
——“對數的概念”之教學設計與思考

●崔志榮 (安豐中學 江蘇東臺 224221)

1 內容分析

“對數”作為高中數學的重點內容之一，有很強的現實意義，它在銀行貸款利息、社會經濟增長率、工程技術、天文學等方面的計算，都有廣泛的應用.它的發明縮短了人們的計算時間，對人們研究科學、了解自然起了重大作用.

“對數的概念”是蘇教版必修1第3章“對數函數”的第1課時，是繼指數函數之后學習的一類新運算.讓學生建立好對數的概念并深刻理解，是后續熟練掌握“對數的運算性質”的保障，是理解并靈活運用“對數函數的圖像與性質”的前提.

2 教學分析

“對數的概念”的教學，重點是一個新概念的生成教學.教材上已經給出對數的概念，很多學生必然事先預習，形成定勢思維，如何引導學生回歸探究，而非生硬接受，是教學的一大難點.

本節課的教學目標是深刻理解對數的概念，如果概念的探究教學時間過長，那么會影響概念反饋理解的時間，學生就不能熟練得出一些簡單對數的值.因此，合理設計探究問題，做到探究與反饋時間的平衡，是對數概念教學的又一個關注點.

基于以上2點分析，筆者對以往的教學過程進行了改進，重新設計教學的各個環節，并已在所教班級試教，自我感覺效果不錯，故把本節課的教學過程、設計意圖、教學反思等整理成文，供讀者在教學中研討.

3 教學過程

3.1 問題情境

題目 某種放射性物質不斷變化為其他物質，每經過1年，這種物質剩留的質量是原來的a倍.設該物質最初的質量為1，請寫出這種物質的剩留量N隨時間b的變化關系式［1］.

學生容易得出ab=N(其中a＞0).

設計意圖 該問題與教材上的例題有所不同:一是幫學生設出相關未知數(物質的初質量、剩留量、時間)，目的是節約時間，讓學生迅速列出關系式;二是將具體數值84%改為字母a，為的是過渡到下面教學設計的3個問題，即在a，b，N中，已知2個量求另一個量.

3.2 合理過渡，自然生成

問題1 在ab=N(其中a＞0)中，已知a，b，求N.

這個問題學生不難理解，若b為整數，則是乘方運算的理解;若b為分數，則是分數指數冪與根式的轉換(在指數函數部分已經學習).

問題2 在ab=N(其中a＞0)中，已知b，N，求a.

師:誰能解決問題2?

生2:當b=0時不能這么做，要單獨考慮，當b=0時，N=1，此時a＞0且a≠1.

師:很好!生1分析出問題2的處理方法，生2又指出其漏洞.需要提醒大家注意的是:如果沒有條件a＞0，那么生1的方法還有點問題，比如x2=N.

生4:x2=N，即x是N的平方根，因為N＞0，N有互為相反數的2個平方根是N的算術平方根.

師:不錯!不過，能不能換個角度理解?

(學生沉默約1分鐘.)

生5:利用函數f(x)=x2的圖像，方程的根是函數值為正數N時，自變量x的取值(教師在黑板上作圖)，因此，只需考察函數f(x)=x2與直線y= N的交點的橫坐標，顯然2個函數有2個關于y軸對稱的交點，把y軸右邊的那個正解規定成

師:我覺得生5的解釋有道理，對于方程實數根的研究，可以把方程轉化為對應的函數，利用函數的圖像研究方程的實數根，這是一種重要的數學思想方法——數形結合.由函數的圖像可知，方程的解取決于正數N的值，數學家在表示這個正數解的時候，就用符號與正數N配合表示成一個新的實數.請大家再理解一下這個數(停頓).

師:另外，在指數的學習過程中，我們已經指出，對于ab=N，通常只研究當a＞0且a≠1時的情況，此時N＞0.接下來，請同學們思考問題3.

問題3 在ab=N(其中a＞0且a≠1)中，已知a，N，求b.

生6:可以用生5的函數方法處理.

師:請具體闡述.

生6:把b看成x，問題3即是解方程ax=N (其中a是大于0且不等于1的常數，N是大于0的常數)，該方程的根，即是指數函數y=ax與函數y=N交點的橫坐標.

師:不錯!同學們畫圖看看方程ax=N的根有什么特點?

生7:不管0＜a＜1還是a＞1，x總有唯一的解.

師:為什么?

生7:因為無論是0＜a＜1還是a＞1，指數函數y=ax都是單調函數，它的值域都是(0，+∞)，又N＞0，所以它與水平直線y=N有且只有1個交點.

教師投影函數圖像(如圖1與圖2所示).

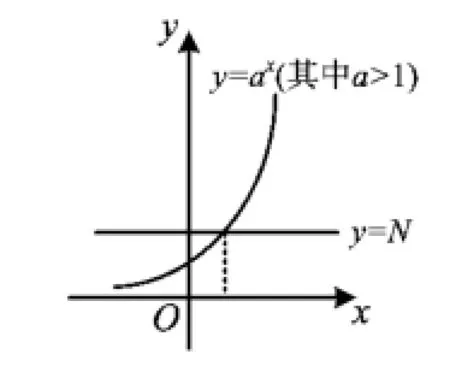
圖1

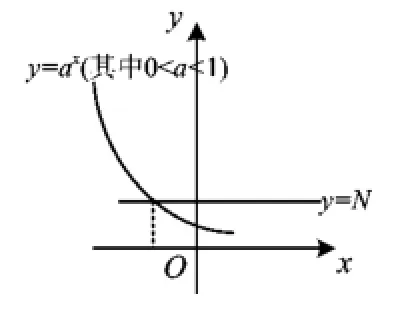
圖2

師:很好!方程ax=N確實存在唯一解，但這個解到底是多少呢?怎樣把它表示出來呢?

生8:這個解應用實數a，N表示，但我不知道怎么表示.

(說明:有不少已預習的學生在下面議論表示方法，學生8沒有預習，不預習的課堂教學效果也精彩［2］.)

師:先不談怎么表示，為什么能用實數a，N表示?

生8:剛才已經分析:方程的解對應著函數交點的橫坐標這個實數，當2個函數確定，交點的位置也就隨之確定，比如若a=2，N=3，則解x就是指數函數y=2x與函數y=3交點的橫坐標，x就必然與2，3相關.

師:有道理!怎樣表示這個實數解呢?我們可以把這個解寫成logaN，這就是我們本節課要研究的“對數”.

(接著是對數概念的描述、板書、理解，到此，總用時約20分鐘.)

設計意圖 問題1的提出，體現的是問題研究的全面性，也體現由易到難的研究過程;問題2的探討，主要目的不是復習指數的運算、平方根的理解，關鍵是要得出一種處理方程問題的思想方法，要探討平方根的表示過程，為問題3的思考作鋪墊;問題3是我們最終的探究目的，要通過問題3建立對數的概念.3個問題過渡自然，既體現循序漸進的原則，又能讓學生認識到問題的關聯性，同時還增強了學生的探究信心.

3.3 交流反饋

交流1 教師要求每位學生獨立寫出5個對數，然后同桌間交流各自的認識.

交流2 教師選取3名學生代表，先從指數、對數的轉換角度來匯報交流自己的認識，此外，學生還可從其他角度理解，不限制思維，教師加以點評.

交流3 教師提出問題，要求學生探究logaab與alogaN的值.首先是4人一組，交流討論;然后由學生代表匯報探究成果.

這一過程用時約15分鐘.

設計意圖 對數的概念雖已建立，但由于學生剛剛接觸，理解不深刻，而且不同的學生理解程度也不同，一些基本功不好的學生更要加強理解.交流1和交流2促進概念的理解提升，尤其對基礎較弱的學生有幫助，交流3能調動學生的探究積極性，培養學生的分析能力.3個交流活動，思維具有發散性，讓每位學生都有事可做，能起到“補差、推中、提優”的分層教學效果.

3.4 練習反饋

從教材、課外資料上選取與對數概念相關的典型練習題(難度不要大，有點小梯度)，學生先練習，教師再對典型的錯誤進行糾正、點評、總結歸納，這一過程約10分鐘.

4 一點反思

問題，是驅動學生思維的源泉!在數學教學中，好的問題可以啟發學生的思維，形成有效的數學探究活動.因此，所設計的問題要符合學生的實際，如果問題過大、過難，則會造成學生無從下手，教師啟而不發;當然，問題過小、過碎，也不行.學生遵循教師的思路(必經之路)，最終達到目的，這樣的引導，學生思維量小，失去“探究發現”的意義［3］.本節課中的問題2，學生雖懂，但要答出生5的方法，還是要經過一番思考才行，問題3學生雖有點陌生，但在問題2的鋪墊與教師的啟發下，學生能有效探究發現.

教學中每一個概念都應當從概念所處的系統出發，促進學生建立新舊概念之間的各種聯系，實現概念網絡的構建與擴展，使新的概念成為學生內部概念網絡的一個有機組成部分.這樣，數學概念教學不再是個別概念的教學，而是通過學生學習概念的各種活動，使學生獲得概念域、概念網絡，直至完成對概念系統的理解與掌握［4］.當學生在原有的理解基礎上學習新概念時，他們就會逐步意識到各個數學問題之間的聯系，他們的理解會更深刻且牢固［5］.本節課正是通過問題1，2，3，將冪的乘方、指數運算公式、平方根以及函數與方程等聯系起來，逐步過渡到建立對數的概念，體現了概念之間的網絡聯系.

［1］ 單墫.蘇教版普通高中課程標準實驗教科書·數學(必修1)［M］.南京:江蘇教育出版社，2012.

［2］ 魏本義.不預習的課堂教學效果也精彩［J］.中小學數學，2012(9):27-29.

［3］ 聶必凱，鄭庭曜，孫偉，等.美國現代數學教育改革［M］.北京:人民教育出版社，2010.

［4］ 李善良.現代認知觀點下的數學概念學習與教學［M］.南京:江蘇教育出版社，2005.

［5］ 全美數學教師理事會.美國學校數學教育的原則和標準［M］.蔡金法，譯.北京:人民教育出版社，2004.