初中數學變式教學的優化探索

范麗娟

【摘要】在現在的初中數學課堂教學中，變式教學是一種常見而重要的教學方法.相應地，它能夠對初中學生進行數學技能和發散思維方面的訓練，進而培養初中學生分析問題和解決問題的能力.因此，本文作者對初中數學變式教學的優化探討這個主題進行了相應的分析.

【關鍵詞】初中數學；變式教學；優化；探討

在經濟轉變和社會形勢過渡的影響下，教育終將成為被關注的方向.縱觀初中數學課堂，變式教學的應用便是教學模式在朝著更有利于教育發展方向邁進的重要見證.它的出現改變了傳統數學課的教學模式，使教學方式更有利于學生的成長和學習，使初中學生從相應“變”的現象中去發現那些“不變”的本質.由于數學本身屬于一門工具課程，不僅被廣泛應用，而且具有這樣的特點，理論多樣，操作復雜.相應地，在初中數學教學中，相應的教學模式存在一定的問題，需要對它進行相應的優化，使它的優勢得以更好地發揮.因此，本文作者對初中數學變式數學的優化進行了相應的分析，以此促進我國教育事業的發展.

一、數學變式教學的概述

總的來說，對于數學教學活動的實施，需要站在學生的角度，對課堂進行相應的設計和優化.相應地，變式教學這種新型的教學模式便是這樣的一種教學模式.在數學教學中，變式教學是對相應的數學問題進行了不同角度、層次、背景、情形的變式.換句話說，變式教學是一種教學設計方法，它揭示了相應問題的本質特征，以此來展現不同知識之間的內在聯系.相應地，具體地來說，所謂的變式教學就是指在教學中，站在一道母題的角度，對母題的問題、條件、設計的數學情景進行相應的改變，并進行重新探討的一種教學方法.變式教學的核心便是利用構造一系列變式的方法，對相應的數學命題進行恰當的轉化，來幫助學生透過現象去對數學的本質特征進行相應的了解.因此，在數學教學課堂中，相應的變式教學扮演著重要的角色.它不僅有利于學生對相應數學概念的理解，還能夠對學生的思維進行相應的拓展，提高他們的學習興趣，以此來使他們相應的能力得以提高.更重要的是，這種變式教學的教學模式能夠讓學生打破原有的思維定式，在變中求進，在進中求通，進行發散思維，來對相應的數學問題進行相應的分析和解決，進而幫助他們更好地去拓展相應的創新空間.

二、運用變式教學推進相應的數學教學

在數學教學中，相應的變式教學是它成長路上很好的助推器，幫助它在坎坷的路上更好地前行.首先，可以利用變式教學來促進數學知識的系統性.所謂的知識系統性主要體現在當下學生學習的知識方面以及前后邏輯的層次性.相應的變式教學可以讓學生形成良好的數學知識結構，促進知識的系統性，對新課標下學生所遇到的數學問題進行很好的解決.其次，利用變式教學促進相應數學能力的發展.在變式教學中，它為學生提供了一個主動進行思維活動的環境.變式教學有利于提高學生的比較和概括能力.如在對“二元一次方程組的解法”進行相應學習的時候，把相應的課后習題和例題進行相應的融合，進而對相應的方程進行相應的變形.這樣便讓學生很清楚地認識到消元的關鍵是方程得變形.除此之外，變式教學能夠消除學習定式的消極影響，有利于學生對知識更好地進行學習.最后，變式教學促進數學思維活動的質量.這主要是因為在變式教學中，學生能夠從多層面、多角度來對相應的數學問題進行探討，進而學生能夠進行相應的創造性思維，相應地，數學思維活動的質量也得到一定程度的提高.

三、初中數學變式教學的優化探討

在初中數學的課堂中，相應的變式教學并不是單一的.在相應的初中數學知識里，它對數學知識的很多方面進行了變式.比如，對相應結論的變式，對相應的解答過程的變式，對相應概念定義的變式，對定理公式的變式.因此，本文作者對初中數學的變式教學進行相應的分析，下面只是其中微小的一角.

1.初中數學中的條件變式法

在初中數學中，條件變式法是變式教學中很常見的，尤其是在對初中數學相應知識概念的教學.它有利于學生對相應數學知識的內涵進行全面的掌握，并進行靈活應用.所謂的條件變式法主要是指對題目問題的已知條件進行相應的改變，以此使相應的問題呈現出不同的形式，激起學生對此問題進行積極的思考，熟悉相應的題型變化.比如，條件變式法在這道初中數學題中的應用.它是一道對一元二次方程根的概念知識點進行相應考查的數學題.例：已知相應的方程x2-ax-3=0的一個根是2，那么a的取值是多少？相應方程還有一個根是多少？對于這道數學題，只需要用代入法就可以求出a的值，在此基礎上，再去求解相應的方程，就可以知道還有一個根是多少.相應地，可以對此題進行相應的改變，引出相應的變式題.對于這道數學題，只需要把相應的常數項-3改為b.即已知方程x2-ax-3=0的一個根是b（b≠0），那么a+b的值是多少？雖然這道數學題的條件和問題有所變化，難度也有所增加，但它所考查的知識點仍然是關于一元二次方程的根.對于這道數學題，還可以進行進一步的變形.即如果b是方程x2-ax-3=0的根，那么b3-2b2-5b+1或者b2+1的值是多少？對于這道相關的變形數學題，可以利用根的定義，再結合等值變形的技巧就可以得出相應的答案.因此，從最初的那道數學題到引申出來的這些相關的數學題中，可以很清楚地知道，利用條件變式法對根的定義進行不同角度的運用，可以幫助學生對相應概念進行很好的掌握和理解.

2.初中數學中變結論的變式題

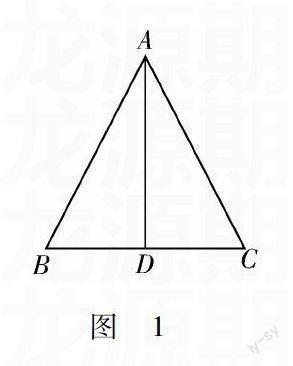
對于初中幾何題，很多學生都是很畏懼的.這主要是因為幾何數學題具有的難度.相應地，在初中幾何數學中，運用變式教學的方式可以減少學生對幾何的恐懼，提高他們對幾何的學習興趣.同時，它還能夠對學生的思維定式進行克制，培養學生對具體問題進行靈活分析的能力，達到舉一反三，觸類旁通的效果.在初中幾何中，變式教學主要是對原有的題目進行相應的圖 1變形，比如，添加、改組、放大、顛倒.例如，△ABC是一個相應的鋼架，AB=AC，AD是連接A和BC中點D的支架.求證：BD=CD.如圖1所示.

對于這道幾何數學題，可以利用“邊邊邊”公理來進行相應的證明，進而可以對這道幾何數學題進行相應的結論變式，進行相應知識的學習和掌握.例如下面四道與之相關的結論變式題：

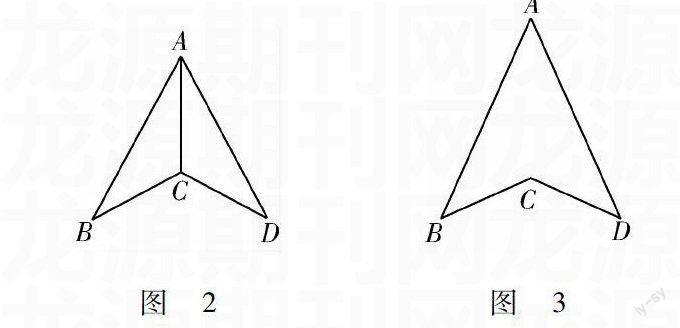
變式1：這道幾何數學題的條件不變，求證：∠B=∠C.變式2：求證：AD⊥BC.變式3：已知，如圖2所示，AB=AD，CB=CD，求證：△ABC≌△ADC.變式4：如圖3所示，AB=AD，CB=CD，求證：∠B=∠C.

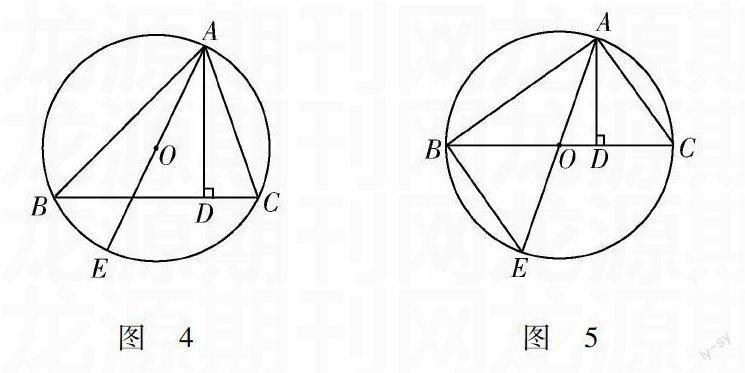
對于這四道引申出來的結論變式題，前面三道都屬于相關的簡單結論變式題，因此，很容易便可以得出相應的答案.但對于第四道相應的變結論的變式題，需要先構建相應的全等三角形，并再此基礎上，添加相應的輔助線來連接AC，進而由相應的△ABC≌△ADC得出相應的結果.相應地，在幾何數學中，相應問題的變化，將會致使相應的思路發生相應的變化.它也不僅僅是論證題，也會有相應的選擇題和填空題出現.它不僅會幫助學生對相應知識點的理解和掌握，還能對他們解題的思路進行相應的改變.例如：如圖4所示，AD是△ABC的高，AE是△ABC外接圓的直徑，求證：AB·AC=AE·AD.

這道幾何數學題主要是對相似三角形的性質進行相應的考查.對于這道幾何數學題，通過對相應問題進行改變，可以變換成相應的選擇題、填空題.例如：已知AD是△ABC的高，AE是△ABC外接圓的直徑，連接BE.那么，圖5中共有（ ）個三角形和△ABC相似.

由這道幾何問題變式數學題得出，由原來的論證題變形為相應的填空題.很顯然，在變式法下，相應的題型也發生了相應的變化.

總之，在初中數學教學中，變式教學是一種非常重要的教學方法.相應地，它不僅能使學生對初中數學的學習產生興趣，還能提高他們相應的能力，培養他們的發散思維.因此，在初中數學教學中，需要把相應的變式教學放在至關重要的位置.最后，作者希望本文在給廣大讀者朋友們帶去幫助的同時，也能引起他們對此新的認識和思考.

【參考文獻】

[1]李忠芳.初中數學變式教學淺析[J].才智，2013（8）：122.

[2]宋遂青.變式法在初中數學教學中的應用[J].學周刊，2013（8）：177.

[3]周海燕.初中數學變式教學淺談[J].中國校外教育，2013（32）：74.

[4]溫河山.初中數學變式教學的方法探析[J].課程教學研究，2012，10：48-50+54.

[5]朱圣東.淺談初中數學課堂變式教學的實踐與策略研究[J].科技創新導報，2012（34）：187.

[6]楊豐采.有關初中數學教學中的變式教學分析[J].中國校外教育，2013（S2）：215.