初中數(shù)學中的數(shù)形結(jié)合思想

宋天華

摘要：數(shù)形結(jié)合作為眾多數(shù)學解題方法中的一種，可以使數(shù)學問題更加直觀、形象地展示在學生面前，有助于學生理解、分析和解決問題，是初中數(shù)學教學中一種重要的解題思想。本文就數(shù)形結(jié)合思想在初中數(shù)學中的應用進行了詳細地探究。

關(guān)鍵詞：初中數(shù)學 數(shù)形結(jié)合 應用

初中數(shù)學是初中教學的重點內(nèi)容，同時也是教學的難點。初中數(shù)學知識與小學數(shù)學知識相比，知識量更大、難度也大大增加，加之數(shù)學知識的片面性和抽象性，學生在學起來具有一定的難度。但是，數(shù)學作為一門研究數(shù)量關(guān)系和空間形態(tài)的學科，它所有的理論知識均是圍繞著數(shù)與形來展開的。而數(shù)形結(jié)合的解題思想則正是充分運用這一點來對數(shù)學問題進行分析和解決。所謂的數(shù)形結(jié)合思想實際上就是利用“形”來直觀地表達和反應數(shù)學問題的本質(zhì)，再用“數(shù)”來對“形”的各種性質(zhì)和變化規(guī)律進行分析和探究。下面就數(shù)形結(jié)合思想在初中數(shù)學中的主要應用進行了探討。

有理數(shù)中的“數(shù)形結(jié)合”

有理數(shù)是初中數(shù)學學習的入門知識，是學生后期數(shù)學學習的理論基礎(chǔ)。在有理數(shù)的教學過程中，如果教師可以引導學生合理地運用數(shù)形結(jié)合的思想，則有利于學生分析和理解所學的數(shù)學知識，拓展學生的數(shù)學思維，提高學生數(shù)學分析能力。而就有理數(shù)的學習階段，數(shù)形結(jié)合思想主要表現(xiàn)在數(shù)軸的應用上，學生如果可以掌握數(shù)形結(jié)合思想，就可以借助數(shù)軸來解決教學過程中所遇到的各種數(shù)學問題，如有關(guān)倒數(shù)、相反數(shù)和絕對值等類型的數(shù)學問題。此外，教師還可以借助生活中常見的物體作為研究對象，來為學生講解有關(guān)的數(shù)學知識。例如，教師可以用溫度計來幫助學生理解數(shù)軸的概念，然后對數(shù)軸上的數(shù)和點的關(guān)系進行明確，讓學生掌握用圖形來分析數(shù)學問題所涉及的數(shù)量關(guān)系，從而達到提高學生數(shù)學解題能力的目的。

例1：已知實數(shù)a、b、c在數(shù)軸上的位置如下圖所示，試化簡下式：

解析：該道例題是數(shù)形結(jié)合思想的最好體現(xiàn)，從數(shù)軸上我們可以明顯地得看出實數(shù)的正負性、各數(shù)之間的大小關(guān)系，從而有利于式子中絕對值跟根號的化簡，而只要將式子中的絕對者和根號化簡掉，就可以明顯地得出有關(guān)的結(jié)論。下面就該道例題的具體解題步驟進行闡述。

解：由題目所給數(shù)軸可知：b<0，c<0，a大于0，且b-c<0，a+b<0，則可得：

，由此即可得到最簡的化簡形式。

函數(shù)中的“數(shù)形結(jié)合”

函數(shù)是初中數(shù)學教學中一個重點內(nèi)容，同時也是一個涉及的知識面最廣的內(nèi)容，尤其是二次函數(shù)問題更是教學的重點內(nèi)容。二次函數(shù)問題通常比較抽象，學生學習的過程中會有一定的困難，所以，大多數(shù)學生不愿意接觸與二次函數(shù)有關(guān)的問題，甚至對其有一種莫名的恐懼感。這樣致使學生形成了一種不正確的數(shù)學解題觀念，非常不利于學生數(shù)學能力的提高。由于二次函數(shù)本身的特性，它與圖形之間具有緊密的聯(lián)系，學生只需要建立直角坐標系，并對題目中函數(shù)的關(guān)鍵點進行定位即可做出有關(guān)的圖形，從而更加直觀、形象地分析問題，這樣將大大地降低學生解題的難度。理論上來講，在二次函數(shù)定義式子（y=ax2+bx+c）中，參數(shù)a決定二次函數(shù)圖形的開口方向，c決定二次函數(shù)圖形與y軸的交點，而二次函數(shù)圖形的對稱性則由參數(shù)a和b所共同決定。因此，如果可以將數(shù)形結(jié)合思想合理地運用于數(shù)學教學中，則可以有效地提高學生解決二次函數(shù)問題的能力。

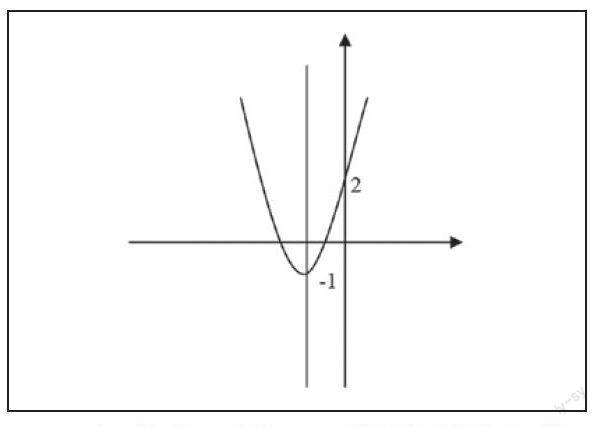
例2：已知點（-1，y1）、（-3，y2）和（2，y3）均在二次函數(shù)y=3x2+6x+2的圖像上，則y1、y2、y3之間的大小關(guān)系為________。

解析：該道例題是一個與二次函數(shù)有關(guān)的大小判斷題，如果學生不懂得利用數(shù)形結(jié)合的思想，則必須要將每個點的x值反代入二次函數(shù)中，分別求出相應的y值，這樣將大大增加工作量。而如果學生可以借助數(shù)形結(jié)合法來做出y=3x2+6x+2的圖形，則可以很快得出y1、y2、y3之間的大小關(guān)系。下面就該道例題的具體解題步驟進行闡述。

解：由二次函數(shù)式y(tǒng)=3x2+6x+2，我們可以將其化簡得出一般的形式，可以得到y(tǒng)=3（x+1）2-1，則可以畫出其對應的簡圖，如下圖所示。

通過圖形我們可以很容易地知道，當x=-1的時候，y值最小，當x=2的時候所取的數(shù)值要比x=-3的時候所取的值大，所以y1、y2、y3之間的大小關(guān)系為：y2>y3>y1

結(jié)束語

數(shù)形結(jié)合思想作為一種解題思想，在初中數(shù)學學習中扮演著重要的“角色”。它可以使抽象的數(shù)學問題直觀化、形象化，有利于學生理解和認識，從而為學生解決數(shù)學問題奠定堅實的基礎(chǔ)。因此，在開展數(shù)學教學的過程中，教師要引導學生樹立數(shù)形結(jié)合的解題思想，從而達到提高學生數(shù)學解題能力的目的。

（作者單位：江蘇省常州市鐘樓區(qū)西林實驗學校）