初中數(shù)學(xué)教學(xué)過(guò)程中化歸思想的運(yùn)用

方曉萍

【摘要】 初中數(shù)學(xué)主要提高學(xué)生對(duì)數(shù)量關(guān)系的認(rèn)識(shí)和對(duì)空間結(jié)構(gòu)的探索，是聯(lián)系初級(jí)數(shù)學(xué)和高級(jí)數(shù)學(xué)的紐帶. 初中數(shù)學(xué)教學(xué)中輔助教師授課，幫助學(xué)生掌握數(shù)學(xué)知識(shí)的主要方法就是教學(xué)中化歸思想的運(yùn)用，將晦澀難懂的數(shù)學(xué)題目變得簡(jiǎn)單、直觀、明了，用簡(jiǎn)化的思想解決難題，提高解題速度，激發(fā)學(xué)生思維的靈活性，節(jié)省思考時(shí)間. 本文從化歸思想和數(shù)學(xué)教學(xué)的結(jié)合入手，分析初中教學(xué)中化歸思想的運(yùn)用.

【關(guān)鍵詞】 初中數(shù)學(xué)教學(xué)；化歸思想；運(yùn)用分析

初中數(shù)學(xué)中的化歸思想是數(shù)學(xué)教學(xué)中運(yùn)用最多、使用最廣的解題方法，能夠最短時(shí)間內(nèi)將數(shù)學(xué)教學(xué)中繁雜的數(shù)量關(guān)系、虛無(wú)的空間跨越、題目中隱藏公式等問(wèn)題變得更加單一、直觀、已知，易于學(xué)生在原有的知識(shí)基礎(chǔ)上深入理解題目?jī)?nèi)容，節(jié)省解題時(shí)間，提高課堂效率，提升教師的教學(xué)水平，增強(qiáng)教學(xué)的有效性.

1. 化歸思想

化歸思想是一種具體的思維方式和解題思路，旨在將復(fù)雜的事情化簡(jiǎn)單，將抽象的事物化具體，將事物間隱藏或者模糊的概念和條件轉(zhuǎn)化成學(xué)生已知的、熟悉的、可以直觀看到的、能夠熟練運(yùn)用的數(shù)學(xué)公式或定理，然后再依據(jù)題目的具體要求，用自己以前學(xué)過(guò)的一系列知識(shí)進(jìn)行解題.

總的來(lái)說(shuō)，就是將數(shù)學(xué)知識(shí)看作一條連接起來(lái)的鏈條，利用和辯證唯物主義的共通性，用發(fā)展變動(dòng)的眼光看待一切問(wèn)題，摸清楚數(shù)學(xué)間的本質(zhì)聯(lián)系，用代入法、配方法、待定系數(shù)法等解題方法進(jìn)行代入和轉(zhuǎn)化，將學(xué)生不熟悉的題目變成實(shí)在的公式，就很容易解決了.

2. 數(shù)學(xué)教學(xué)過(guò)程中化歸思想的運(yùn)用

2.1 提高學(xué)生的化歸意識(shí)

首先，培養(yǎng)學(xué)生重視化歸思想. 教師進(jìn)行數(shù)學(xué)教學(xué)時(shí)，要有意識(shí)地對(duì)學(xué)生進(jìn)行提醒和重申，先引起學(xué)生對(duì)化歸思想的被動(dòng)重視，然后逐漸進(jìn)行滲透教育；或者變化數(shù)學(xué)問(wèn)題形式，將幾何和代數(shù)的問(wèn)題在兩者之間相互轉(zhuǎn)化，將條件眾多的復(fù)合型題目變成簡(jiǎn)單易懂的題目，并多次在教學(xué)實(shí)例中運(yùn)用化歸思想進(jìn)行解題，增強(qiáng)學(xué)生的化歸意識(shí).

其次，加強(qiáng)化歸思想的應(yīng)用. 在課堂上，要求學(xué)生先用自己的方法解決一道問(wèn)題，然后教師運(yùn)用化歸思想重新解題，讓學(xué)生有一個(gè)直觀的對(duì)比，用兩者之間的差距讓學(xué)生明確化歸思想的便捷性；在布置作業(yè)方面，多布置同類型的作業(yè)，增強(qiáng)學(xué)生運(yùn)用化歸思想解題的實(shí)踐次數(shù)，讓學(xué)生無(wú)意識(shí)地將這種思想方法作為習(xí)慣性的解題方法.

2.2 在初中數(shù)學(xué)教學(xué)中運(yùn)用化歸思想

2.2.1 復(fù)雜簡(jiǎn)單化

在數(shù)學(xué)的學(xué)習(xí)中，最難的就是復(fù)雜的復(fù)合型題目，非常讓學(xué)生頭疼. 遇到這種問(wèn)題，就要學(xué)會(huì)利用化歸思想將題目中無(wú)用的句子進(jìn)行刪減，總結(jié)出一條清晰明了的問(wèn)題線，找準(zhǔn)關(guān)鍵信息，明確題目要求，然后再進(jìn)行解答. 如下面的案例：

例1：山羊和綿羊各自馱著貨物在主人后邊走著，山羊不停地發(fā)牢騷，說(shuō)主人偏心，自己背上的貨物太重，快要走不動(dòng)路了. 綿羊說(shuō)：“你瞎嘀咕什么呢？我的比你的還要重，我都還沒(méi)說(shuō)話呢，如果你給我一袋，我馱的就是你的兩倍了，知足吧！”山羊就反駁說(shuō)：“你再給我一袋，我們就一樣多了. ”問(wèn)：山羊和綿羊各自馱著幾袋貨物？

當(dāng)學(xué)生一眼看到這道題目時(shí)，就會(huì)覺(jué)得頭腦一懵，字?jǐn)?shù)太多，條件理不清，也就無(wú)法正確解題了. 反之，摒棄以前的解題方法，用化歸思想重新看這道題，將綿羊和山羊背上馱的貨物分別設(shè)成x和y，根據(jù)題目中的條件“如果你給我一袋，我馱的就是你的兩倍了”和“你再給我一袋，我們就一樣多了”列出具體的方程式：x + 1 = 2（y - 1），y + 1 = x - 1，然后聯(lián)立方程組，解得x = 7，y = 5. 這樣一來(lái)，就將題目中的復(fù)雜條件轉(zhuǎn)化得很簡(jiǎn)單，至于計(jì)算也就不成問(wèn)題了. 所以，在遇到比較難的數(shù)學(xué)問(wèn)題時(shí)，要運(yùn)用化歸思想，將復(fù)雜的事物簡(jiǎn)單化，能夠達(dá)到事半功倍的效果.

2.2.2 挖掘隱藏的已知條件

有些數(shù)學(xué)問(wèn)題，出題者會(huì)在題干上有意地隱藏已知條件，并不會(huì)出現(xiàn)直觀的信息，這就需要學(xué)生深挖，仔細(xì)閱題，考慮在問(wèn)題深處的原本已經(jīng)學(xué)過(guò)的定理或者公式，將它們運(yùn)用到本次解題過(guò)程中，這也是化歸思想的一種運(yùn)用手段，將隱藏的條件直觀化，幫助更快地解答問(wèn)題.

例2：一個(gè)多邊形的內(nèi)角和減去其外角和得到180度，問(wèn)：這個(gè)多邊形是幾邊形？

這個(gè)案例考查的是學(xué)生對(duì)于多邊形內(nèi)角和與外角和的掌握，利于以往知識(shí)的回顧：多邊形的內(nèi)角和為（N - 2） × 180，其外角和為360，因此可以得到解答公式：（N - 2） × 180 - 360 = 180，最后解題得解N = 5.

由此可見，用化歸思想解題，能夠綜合題干所給條件和隱藏的信息，作為已知的解題輔助，既能夠讓學(xué)生回顧以往知識(shí)結(jié)構(gòu)，補(bǔ)充自身的不足之處，又有助于明確解題思路，加快答題過(guò)程.

2.2.3 抽象直觀化

化歸思想還有一個(gè)優(yōu)勢(shì)就是能夠?qū)⒊橄蟮氖挛镒兊镁唧w化，將含糊不清或者難以直觀表現(xiàn)出來(lái)的題目用表格或者其他讓學(xué)生容易理解、容易接受的方式表現(xiàn)出來(lái)，理清思路.

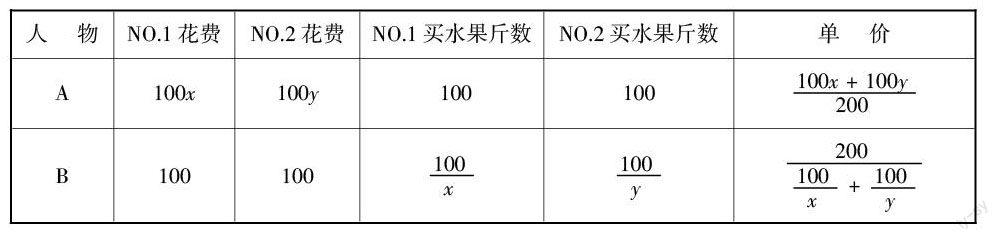
例3：A，B兩個(gè)人兩次在同一家水果店買水果（假設(shè)他們兩次買的水果單價(jià)不同），A每次買100千克的水果，B每次買水果用100元. 如果假設(shè)A，B兩人第一次買水果的單價(jià)為每千克x元，第二次買水果的單價(jià)為每千克y元. 若誰(shuí)兩次買水果的平均單價(jià)低，誰(shuí)的購(gòu)買方式就更合算. 問(wèn)：A，B兩個(gè)人誰(shuí)買水果最合算？

要解這個(gè)問(wèn)題，需要用表格輔助，將題目中抽象的條件真實(shí)直觀地放在學(xué)生面前，根據(jù)題目?jī)?nèi)容，可以得出下圖：

化歸思想在初中數(shù)學(xué)教學(xué)中的運(yùn)用，能夠?qū)⒛切┳屓烁械絽挓┑臄?shù)量關(guān)系和空間結(jié)構(gòu)用合理的轉(zhuǎn)換樣式將題目信息形象、生動(dòng)、具體地表現(xiàn)出來(lái)，根據(jù)學(xué)生原有的知識(shí)結(jié)構(gòu)發(fā)散思維，開拓創(chuàng)新；能夠順利理清題目所給的條件和要求，將各種信息連接起來(lái)，用變化、發(fā)展的眼光看待問(wèn)題，進(jìn)而快速高效地解決數(shù)學(xué)難題.