高中生數學辨析能力培養活動開展芻議

李媛

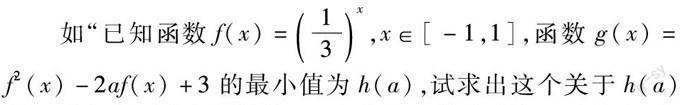
【摘要】辨析能力是數學思維能力的內涵之一.高中數學學科是思維的藝術，培養數學辨析能力是其任務之一.高中生需要通過思考、研析、判斷、歸納等實踐活動，掌握數學知識，提升數學技能.這就需要高中生既要會思考分析數學問題，又要會綜合考慮，辨別判斷數學學習活動.本文作者在此簡要論述了高中數學課堂教學中，高中生數學辨析能力培養活動的所采取的一些方法舉措.

【關鍵詞】高中數學;辨析能力;培養活動;芻議

學習能力培養，是新課程改革下高中階段各個學科所肩負的重要使命，也是每個任課教師所承擔的重要任務.數學是思維的藝術，需要良好的概括、判斷、推理和歸納等數學學習能力.教育學認為，數學辨析能力作為數學學習能力的一個重要方面，不僅包含了分析、思考、概括的“析”的能力，同時還包含了判斷、甄選、研析、闡述的“辯”的能力.高中生在數學學科的學習進程中，經常圍繞學習探知活動效能的優劣、解析問題案例方法的繁簡以及探究實踐活動的表現等等方面，進行深刻的反思和認真的剖析.這一過程中，就需要高中生良好的數學辨析能力作為“保證”.新課程改下，既會“思”，又會“析”的高中生，成為高中數學教師培養的重要方向.本人在此簡要論述高中數學課堂教學中，高中生數學辨析能力培養活動的方法舉措.

一、在共同探知數學知識內容中，培養數學辨析能力

學習新知，是學生學習能力培養必不可少的一個環節.學生辨析活動，需要數學知識內容作為“依據”，用事實講話，用知識佐證.同時，教育實踐學認為，學習對象在數學知識內容的學習探知中，所開展的思考分析活動，也為辨析活動開展打下了“基礎”.高中生在探知數學知識內容的進程中，在教師的有效指引下，通過思考、研析、判斷、推理等數學思維活動，對數學知識內容進行了深刻的感知和研析，從而抓住了數學知識“精髓”和要義，其數學辨析能力也在此過程中得以訓練和提升.因此，高中數學教師應將數學知識探析活動，作為培養高中生數學辨析能力的重要部分，引導高中生圍繞數學知識點內容進行深入的研究、思考和分析，同時，組織高中生對自身及他人的探知數學知識活動進行深刻的評析和判斷，提升其數學辨析能力.

如“等比數列的前n項和的公式”知識點教學中，教者采用互動式教學方式，通過設置“前n項和Sn=a1+a1q+a1q2+…+a1qn-1，如何化簡？”、“如何處理（1-q）Sn=a1-a1qn”等問題，學生經過思考后，提出能否借助于推導等比數列的通項公式的方法列出等式，然后迭乘或迭加.教師根據高中生探知活動現狀，組織高中生闡述所獲得的認知內容，并讓其他學生進行實時的補充，以此促動其他高中生深入分析、判斷獲取內容的正誤以及學習活動的表現，完善和提高高中生數學知識素養.

上述新知教學活動中，高中生在雙邊互動的共同合作中，通過教師的有效“引”和學生的深入“探”等協作“勞動”，指導和推進高中生探知該知識點的活動進程，同時，高中生在“回頭看”探究研習數學知識內容的過程中，自我反思、深刻辨析能力得以有效鍛煉.

二、在深刻研析案例解析方法中，培養數學辨析能力

案例教學，為高中生提供了鍛煉數學技能的“載體”，同時，也為教師提供了有效教學的“抓手”.教育學指出，高中生學習能力，可以通過數學案例解析活動，得以有效培養和顯著提升.因此，高中數學教師應將數學案例作為數學辨析能力培養的有效抓手，延長案例教學活動的過程，在解析案例活動基礎上，就總結歸納得出的解析策略開展思考研析活動，組織高中生對解析案例的過程以及所采用的方法進行深入思考、細致辨析、深刻判斷，在共同研析、深刻辨析中，形成正確解析方法和思路，提升數學辨析能力.

如“已知函數f（x）=13x，x∈[-1，1]，函數g（x）=f2（x）-2af（x）+3的最小值為h（a），試求出這個關于h（a）的函數解析式”案例教學中，高中生在認真研析、思考中、在悉心指導、講解中，得出其案例的解題思路為：“根據題意，可以知道g（x）為關于f（x）的二次函數，可以采用換元法解題方法，將函數轉化為求特定區間內的二次函數最值問題，分類討論區間動軸”，解析策略為：“采用轉化的解題思想，結合函數圖像，定軸動區間，定區間動軸”.在總結評講環節，教師將教師的評講活動進行變為學生的反思辨析活動，組織高中生進行對比分析，找出解析活動中自身存在的不足以及自己的認知感受，引導高中生“說”出思維辨析的過程和自己的點滴認知感受，讓高中生準確掌握解析案例的方法，有效鍛煉其數學辨析能力.

三、在反思評析學習活動效能中，培養數學辨析能力

教育發展學指出，不同學習階段的學習對象，與對應的學習階段學習目標要求之間存在差距，是客觀存在的現實.高中生數學學習能力，教師可以通過反思評析學習活動效能這一活動，進行有效的培養和提升.眾所周知，高中生在反思評析自身學習活動過程中，不僅要對自身的學習過程表現進行“剖析”，同時還要對自身的思維探析過程進行“辨析”.因此，高中數學教師要注重評價教學活動的開展，在每一環節結束后，或整個課堂教學活動結束后，組織高中生認真的“回頭看”，采用自主反思評析、生生相互評判、師生互動評價等形式，引導高中生結合探知、實踐體會和收獲，認真辨析、思考自身在學習探知、探究分析中的表現和效果，認識學習存在不足，形成正確解題策略，并能夠通過“說”的方式，進行有效展示和呈現，以此鍛煉高中生的辨析能力.如“在銳角△ABC中，若tanA=t+1，tanB=t-1，試求出t的取值范圍”案例講解中，教師組織高中生對解析活動進行辨析.高中生在辨析過程中，經過認真反思，認識到解題中存在“忽視問題條件，只注意到tanA>0，tanB>0的條件，沒有注意到tanC也必須為正的情況”不足，并指出在解答此類問題時，需要注意“全面認清問題條件所隱含的條件內容，并能結合三角函數的相關知識進行解析”，高中生的數學辨析能力能夠在評析反思的過程中得以有效鍛煉和提升.

總之，數學辨析能力作為數學學習能力的內涵之一，高中數學教師要遵循高中生認知規律，將培養活動落實在教學活動之中，巧借有效載體，精心開展教學，實現高中生數學辨析能力在有效教學中切實鍛煉和有效提升.