美術生數學思維困惑的淺要分析

于炳友

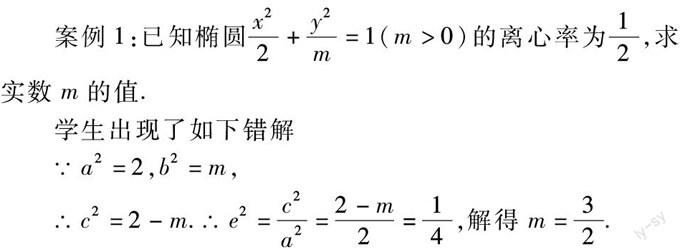
【摘要】當今高考美術熱已經成為了一個不爭的事實，而美術生的文化課尤其是數學課的學習怎樣才能高效達標？怎樣提高我們高中美術生數學教學的有效性？本文將對美術生數學解題困惑的成因及解決方法作簡要的分析，對常見題型的典型錯誤做簡要的歸納.

【關鍵詞】美術生數學思維;數學解題困惑;典型錯誤

江蘇新課改的實施使我們傳統的課堂教學模式發生了很大的變化：要求教師由單純的知識傳授者變為學生學習興趣的發現者與管理者、變為了師生共同探索知識的合作者和學習者.教學內容的選取更加密切聯系社會實際和學生生活實際，學生的學習普遍采用自主、合作、探究的方式，先實際動手操作，遇到問題后學生積極主動找老師請教、找同學討論，真正解決問題.師生之間關系自由、和諧、民主、平等.

然而，在我近幾年對美術生的數學學習過程的觀察中發現很多問題，美術生長期的藝術專業訓練使其數學思維方式發生了一定的變化，長期的模仿使其解題時的思維缺乏創造性.往往他們用他們剛剛入門的藝術的眼光去尋找數學的美感，而其數學專業知識積累的量又不夠，數學里的邏輯美又尋找不到，這時學生的數學學習興趣就會逐漸喪失，學生會產生巨大的心理落差，甚至對數學學習有恐懼感，他們常用一句話概括了自己的現在乃至今后的數學水平，“我數學不好啊”而不去尋找究竟是哪個章節，哪個知識點學的不好.因此，研究美術生的數學思維困惑對于美術生數學教學是十分必要的.

一、高中美術生數學解題困惑的形成原因

我們知道，數學思維是指人用頭腦進行邏輯推導的屬性，能力和過程，它反映的是數學的本質及思維規律性.而所謂高中美術生數學思維，同樣是指學生在對高中數學感性認識的基礎上，運用分析，歸納思維的基本方法，理解并掌握高中數學內容而且能對具體的數學問題進行論證與判斷，從而獲得對高中數學知識本質和規律的認識能力.美術生的數學解題思維存在著困惑，這種解題思維的困惑的成因，一部分是由于我們教學中的疏漏，但更多的則來自于學生自身的思維品質的養成不好，來自于學生中不成體系的知識結構和欠缺的思維模式.

如果教師的教學脫離學生的基礎，只顧自我欣賞，在我陶醉;如果學生在學習高中數學過程中，其新舊數學知識不能順利銜接，只顧抄記筆記，不去總結.那么這時就勢必會造成學生對所學知識認知上的不足、理解上的偏頗，從而在解決具體問題時就會產生解題困惑，影響學生解題能力.

二、美術生數學思維困惑的具體表現

由于美術生數學思維困惑產生的原因各不相同，所以他們數學思維困惑的表現各異，具體的可以概括為：

1.數學思維膚淺：由于美術生多數不能脫離具體表象而形成抽象的思維，自然也無法擺脫局部事實的片面性而把握事物的本質.如在蘇教版選修1-1橢圓教學時出現了如下典型錯誤：

案例1：已知橢圓x22+y2m=1（m>0）的離心率為12，求實數m的值.

學生出現了如下錯解

∵a2=2，b2=m，

∴c2=2-m.∴e2=c2a2=2-m2=14，解得m=32.

學生這種錯誤的形成是因為他們在做橢圓題目時多數都是焦點在x軸上，這樣他們已經形成了一種思維定式，即便這種思維不一定正確.所以，我們教師在教學中一定要反復叮囑學生，討論橢圓方程，要注意焦點位置

2.缺乏足夠的數學思維能力：忽略了隱含條件，不能轉化為已知的數學模型或過程去分析解決.在學習蘇教版選修1-1雙曲線教學時出現了如下典型錯誤：

案例2：設雙曲線中心在原點，焦點在y軸上，ca=52，若點P（0，5）到雙曲線上的點的最短距離為2，求雙曲線方程.

學生出現了如下錯解：由e=52知，e2=c2a2=1+b2a2=54， ∴a2=4b2，∴設雙曲線方程為y24b2-x2b2=1.

設P到雙曲線上的點（x，y）的距離為d，

則d2=x2+（y-5）2=14（y2-4b2）+（y-5）2=54（y-4）2+5-b2.

當y=4時，d2min=5-b2=4，∴b2=1，a2=4，

∴雙曲線方程為y24-x2=1.

實際上本題由雙曲線方程中的自變量取值范圍可知y≥2b，因此必須將b視為參數，在求d2的最小值時進行分類討論.

由此可見，美術生數學思維困惑及解題困惑的形成，不僅不利于學生數學思維的進一步發展，而且也不利于學生解決數學問題能力的提高.所以，在平時的數學教學中注重突破學生的數學思維困惑就顯得尤為重要.

“書越來越難教，美術生更難教”，這是我和部分同事的感慨.怎樣才能避免在課堂上唱獨角戲，怎樣才能激發美術生的數學學習興趣？怎樣改變很多教師“求學生學”“哄學生學”的現狀？怎樣才能真正的讓學生做到踏實“求學”？其實，只要我們堅持以學生為主體，了解美術生的學習特點、思維特點、了解他們的學習習慣，以培養他們的數學思維發展為己任，則勢必會真正提升美術生數學教學質量.