不容忽視的知識獲得途徑

☉江蘇省如皋經濟開發區袁橋初級中學 顧亞琴

不容忽視的知識獲得途徑

☉江蘇省如皋經濟開發區袁橋初級中學 顧亞琴

信息技術給初中數學課堂教學帶來了巨大變革，信息技術應用成為很多數學老師進行教學的“必殺技”.大量信息技術在數學教學活動中的應用，不僅豐富了數學的學習內容，還豐富了學生獲得數學知識的方式.在當下的課堂中，教師一般會以課件為“四基”載體，以投影交流為主要互動方式，引領學生展開數學學習，由于教者的精心設計，一般都能取得不錯的教學成效.但是，值得注意的是：在信息技術大量涌入課堂的過程中，一些傳統的獲得知識的有效途徑正被逐漸“邊緣化”.板書，就是眾多被邊緣化的傳統獲得方式之一.在近期觀摩隨堂課時，筆者發現板書的“淡化”已成“燎原之勢”.這樣的“淡出”引發了筆者的思考：在信息技術下的課堂教學中，板書的哪些教學功能依然有效呢？本文將從這幾節課中的板書入手，談談筆者對此的思考，希望能給您帶來啟示.

一、幾節隨堂課的板書現狀

1.用課件無板書，黑板上“干干凈凈”

Z教師在執教人教版八年級上冊“12.1全等三角形”時，從欣賞圖片入手，歸納出“全等形”及“全等三角形”的定義，并通過課件展示出來.為了展示全等三角形的獲得過程，教者再用課件分別展示了一個三角形的平移、翻折與旋轉的過程，讓學生在體會圖形變換過程中的變與不變的同時，揭示出全等三角形的對應頂點、對應邊、對應角等概念.同樣還是利用課件，教者將兩個全等三角形進行了疊合演示，學生通過觀察歸納出了全等三角形的性質，教師將性質進行了投影.接下來，Z老師繼續用課件呈現鞏固練習，讓學生應用本節課所獲得的新知解決一些簡單的數學問題.應該說Z老師的教學流程清晰，課件設計精美，為學生獲得本課的“四基”起到了很好的輔助作用.但自始至終，教師沒有在黑板上寫一個字，無論是全等形、全等三角形的定義，還是全等三角形的性質都沒有板書，甚至連課題都未曾在黑板上呈現，這種“純正”的替代，讓課件成為學生獲取知識的唯一通道.板書的棄用，讓學生失去了一個行之有效的知識獲得渠道，讓人感到十分可惜！

2.講到哪兒寫到哪兒，黑板上“亂七八糟”

在教學人教版“24.1.3弧、弦、圓周角”一節時，W老師將課件作為教學的主體，板書成為了課件“漏洞”的補充.課上，W老師首先用課件將課本中的“探究”呈現出來，讓學生剪圓形紙片并將紙片繞著圓心旋轉，要求他們在探究中嘗試歸納結論.可能是課件設計時失誤，也可能是學生的生成超出了教者的預設，學生陳述的結果并未在課件中得到展示.教師發現課件不能呈現后，立即板書：“圓是軸對稱圖形，直徑所在的直線是它的對稱軸；圓還是中心對稱圖形，圓心是它的對稱中心”.接下來，投影圓心角的定義，并請學生結合投影辨析“在給出的四幅圖中，哪些角是圓心角”.接下來，教師投影“學生活動”：探究“在同圓或等圓中，相等的圓心角所對的弧、所對的弦分別有著怎樣的關系”.在學生探究得出結論后，教師在黑板上隨意選擇了一塊地方將定理的說理過程呈現出來，將推論的說理過程也一并進行展示.此時，黑板上文字、圖形、符號互相交錯，幾乎布滿了整個黑板.雜亂無章的板書毫無美感可言，無序的板書，讓學生認知的主線得不到凸顯，完整的認知歷程并沒能將新知有序地融入到學生的已有知識網絡之中.僅從教學成效的角度分析，這樣的板書呈現是失敗的.

3.寫了擦擦了寫，黑板上“不斷更新”

在教學“22.2二次函數與一元二次方程”時，L老師首先投影“一次函數與一元一次方程”的認知歷程，將一次函數與一元一次方程、不等式（組）間的關系在黑板上進行了板書，此時板書已經占據了大半個黑板.接下來，教師引入課題并進行了板書，在書寫課題的同時他也順手將剛才的板書擦去.投影教材中的“問題”（即擊球問題，詳見人教版九年級上冊教材第43頁），板書函數關系式h＝20t-5t2，請學生說說問題解決的方法.一生陳述：結合圖像來答較好.于是老師在黑板上畫出了小球飛行的路線，學生對照圖像分別給出了四道題的求解過程，教師將學生說出的四個方程“15＝20t-5t2”“20＝20t-5t2”“20.5＝20t-5t2”“0＝20t-5t2”逐一板書，并將解方程的過程和答案也分別寫在黑板上.不一會兒，黑板又滿了.為了板書根據四個方程歸納出的“一次函數與一元二次方程的關系”，四個方程的解答過程很快被擦去.接下來，教師用投影呈現了“鞏固練習”，為了讓學生能將解題過程展示出來，教師將板書再次擦去，“騰”出地方給學生板演.整個課堂教學過程中，板書四度更新，到最后留下的是學生鞏固練習的過程.教師在一次次擦除與重寫中，努力引領學生回顧舊知、呈現新知并進行鞏固應用.這種沒有規劃的“寫擦交替”，學生所能感知到的知識在不斷更新，但他們無法感知到知識間的關聯，著實對知識的網絡化建構不利.

二、信息技術下板書的教學功能分析

信息技術的引入，為學生獲取數學知識增加了一條途徑.大容量的教學課件進入課堂，豐富了教學內容和教學方式，看似弱化了板書的作用，實則對教師教學板書的設計提出了更高的要求，迫使教師呈現在黑板上的內容“字字重要”，每一個板書都指向教學目標，服務于學生的學習，為他們獲取知識與應用知識提供了充足的便利.

1.固定核心知識，便于學生提取應用

課件演示是即時的，翻過一個頁面，前面的知識就成為了“歷史”.隨著頁面不停翻動，教學進程不斷向前推進，一些核心概念和核心方法也會隨之逐漸“淡出”學生的視野，此時，適時將一些核心知識和方法板書，將會讓它們在黑板上“定格”，確保學生在課堂學習中后續應用時“有據可依”.

案例1：一位老師在教學“4.1.2直線、射線、線段”時，在學生自主“作圖”探究歸納出“經過兩點有一條直線，并且只有一條直線”的基本事實后，教師立即將這一結論及其簡述“兩點確定一條直線”用板書呈現.接下來，投影植樹、射擊、砌墻等生活中的實例，讓學生感知“先定兩點，再定直線”的基本事實的應用，在逐次呈現完整的“直線植樹”“筆直砌墻”“精準射擊”后，教師追問：這么做的數學道理是什么？學生立即想到了黑板上的基本事實，在師生的互動交流中，這一核心知識被不斷強化，接下來的“用兩點表示直線”的早期表象自此建立起來.

案例分析：本課的教學內容很多，知識十分碎，既有直線、射線、線段的抽象過程，又有基本事實的生成過程，加之三種線的符號表示，但教者緊扣核心主線（即“兩點確定一條直線”的基本事實），將全課知識圍繞其展開.板書，讓這一核心知識及時“定格”，給學生進一步獲取新知和對新知的鞏固應用帶來了極大便利.如此板書，符合學生的認知需求，順應了教學方向，值得推廣.

2.展示解題過程，強化范例摹寫與個案矯正

基于課件演示過程中頁面的稍縱即逝，讓學生對一些解題范例的認知與摹寫不能十分到位.此時，用板書將例題的解題過程展示出來，恰好能彌補信息技術應用的不足.通過在黑板上的范例展示，規范的過程完整地固定在黑板上，一方面有利于學生對照范例進行摹寫，呈現出與范例相近的解題過程，另一方面，還能讓學生對比范例矯正自己的過程.

案例2：“22.2.1配方法”教學片斷.

探究：怎樣解方程x2+6x+4=0？

在師生互動交流下，教師將解題過程進行了板書，如圖1.

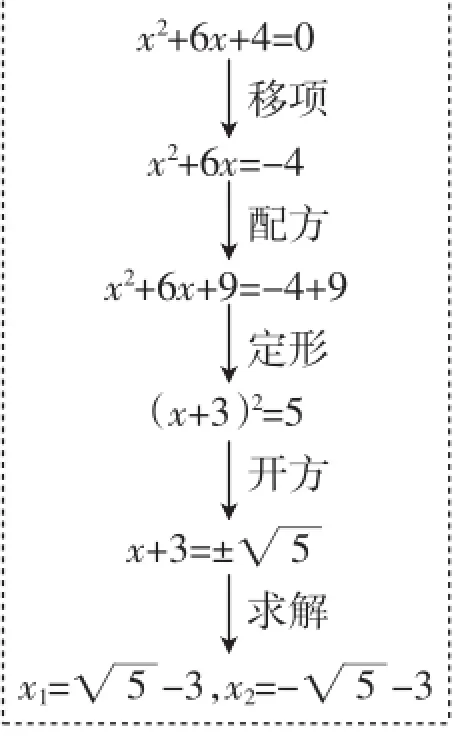
圖1

板書結束后，教師請學生仿照圖1中的解題過程用配方法解方程x2-8x+1=0.學生參照板書的范例自主解方程，并在小組中交流.5分鐘后，組內交流結束，部分學生再度參照范例矯正自己的解題過程.

案例分析：配方法是解一元二次方程的重要方法，用這種方法解方程有著規定的流程.因此，在教學中，借助板書“易于定格”的特點，教者將“用配方法解系數為1的一元二次方程”的過程完整呈現在黑板上，為學生提供了一個解題“參照”.這樣的展示，學生可以參照“范例”進行“摹寫”，按部就班地給出用配方法解x2-8x+1=0的過程.除此之外，組內交流時，板書還是學生評價的參照，他們可以對照范例對同組同學的過程進行評價；自主訂正時，板書還是出錯的學生自我矯正的范本.

3.逐步呈現新知，推動知識融合與網絡建構

新知的生成必須建立在舊知的基礎之上，板書作為信息技術的重要補充，它是學生獲取數學知識的重要途徑，“必要的板書有利于實現學生的思維與教學過程的同步，有利于學生更好地把握教學內容的脈絡”.因此，在教學過程中，我們應“遞進”呈現教學板書，以便學生逐步將新知與舊知關聯起來，促進知識間的融合，建構出有效的知識網絡.

案例3：“相似三角形的性質”教學片斷.

本課是基于相似三角形判斷基礎之上對相似三角形的再認知，學生已經獲得“相似三角形的對應邊成比例，對應角相等”的性質.課上，教師首先引導學生回憶相似三角形的判定方法及已獲得的性質，并將兩個性質進行了板書.接下來，投影圖2，并讓學生探究圖中的相似三角形ABC和A1B1C1的兩條高AD和A1D1的關系.

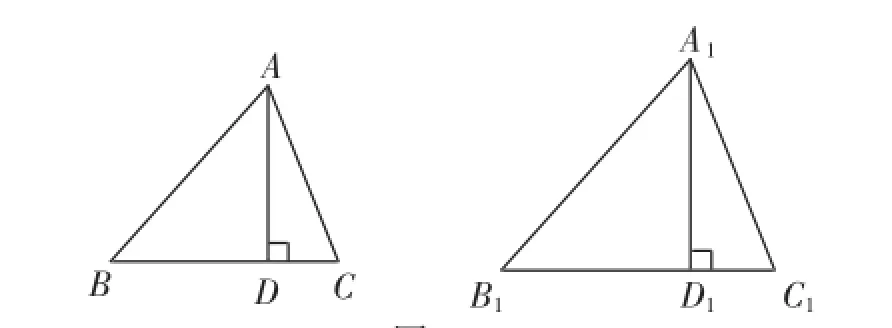
圖2

學生根據已有的知識進行探究，并迅速給出了結論.此時，教師在原有性質的下方，補充板書“相似三角形對應高的比等于相似比”.

按照同樣的教學流程，通過師生互動，教師先后將相似三角形對應中線、對應角平分線的性質進行了板書，并提出問題：你能用一句話概括出相似三角形中這些對應線段的性質嗎？學生歸納，教師板書：相似三角形對應線段的比等于相似比.

案例分析：“相似三角形對應邊的比相等，都等于相似比”，這是學生的舊知，本節探究的其他性質均建立在性質基礎之上.因此，教師首先將這一性質板書，并以此為起點探究了其他性質.教師的板書從學生的認知起點出發，在知識的獲得過程中，將新知與舊知的關聯在黑板上呈現出來.這樣的板書，讓學生在獲得單一知識過程中，快速融合相似三角形的性質與判定的知識，有效促進了相似三角形板塊的知識網絡的建構.這種循序漸進式的板書，順應了學生獲得知識的需求，取得了很好的教學效果.

三、寫在最后

板書，是數學課堂教學的重要組成部分，信息技術進入課堂后，對教學板書的設計提出了更高的要求，板書數量不斷減少，但質量卻不斷提升.教師通過有限的教學板書，呈現給學生的應該是課堂教學最重要的，也是數學認知最核心的知識，不僅要有利于學生獲得數學知識，同時還要為他們提取和應用這些知識提供便利，促進這些數學知識的網絡化建構.因此，我們要立足學情，緊扣教學內容，合理設計板書，力求板書精品化，用少量的文圖，呈現易于被學生記憶、模仿及應用的知識與情境，全面提升學生獲取數學知識與應用數學知識的能力！