理解“三個(gè)理解”凸顯數(shù)學(xué)思想

☉浙江省紹興市上虞區(qū)實(shí)驗(yàn)中學(xué) 黃文光

☉浙江省紹興市上虞區(qū)教體局教研室 酈興江

理解“三個(gè)理解”凸顯數(shù)學(xué)思想

☉浙江省紹興市上虞區(qū)實(shí)驗(yàn)中學(xué) 黃文光

☉浙江省紹興市上虞區(qū)教體局教研室 酈興江

人民教育出版社中數(shù)室章建躍先生提出的“三個(gè)理解”是指“理解數(shù)學(xué)、理解學(xué)生、理解教學(xué)”，其具體要義詳見(jiàn)文1.理解數(shù)學(xué)是提高教學(xué)質(zhì)量的前提，只有理解數(shù)學(xué)，才能準(zhǔn)確地確定教學(xué)目標(biāo)與任務(wù)，從而在目標(biāo)的驅(qū)動(dòng)下，準(zhǔn)確解析教學(xué)任務(wù)中所蘊(yùn)含的數(shù)學(xué)思想；理解學(xué)生是實(shí)現(xiàn)有效教學(xué)的基礎(chǔ)，只有理解學(xué)生，才能立足于學(xué)生的“最近發(fā)展區(qū)”，用學(xué)生的眼光對(duì)待數(shù)學(xué)教學(xué)，向?qū)W生有機(jī)滲透數(shù)學(xué)思想和方法；理解教學(xué)是實(shí)施有效教學(xué)的關(guān)鍵，只有理解教學(xué)，才能有效實(shí)現(xiàn)教與學(xué)的和諧統(tǒng)一，在這個(gè)統(tǒng)一體中努力實(shí)踐數(shù)學(xué)思想的感悟與內(nèi)化.本文擬以對(duì)“三個(gè)理解”的理解為討論視角，對(duì)文中所引用的案例進(jìn)行剖析與微議，以此來(lái)反觀在“三個(gè)理解”視角下的數(shù)學(xué)思想在教學(xué)中的重要地位與作用.

一、理解數(shù)學(xué)內(nèi)涵，著意解析數(shù)學(xué)思想

數(shù)學(xué)思想具有比較隱喻的特點(diǎn)，它蘊(yùn)含于知識(shí)內(nèi)部，要經(jīng)過(guò)反復(fù)地體驗(yàn)與揣摩才能領(lǐng)悟和運(yùn)用.數(shù)學(xué)思想方法的教學(xué)，必須要對(duì)教學(xué)內(nèi)容進(jìn)行細(xì)致的分析，對(duì)教材文本進(jìn)行深度的解讀，分析出其中所蘊(yùn)含的數(shù)學(xué)思想方法.比如“數(shù)軸”一課的教學(xué)，這是學(xué)生進(jìn)入初中首次遇到的有關(guān)數(shù)形結(jié)合的一個(gè)好載體、好工具.浙教版教材是用生活中的溫度計(jì)作為教學(xué)實(shí)例來(lái)引入的.在教學(xué)中，一方面教師要引導(dǎo)學(xué)生進(jìn)行高度抽象：將實(shí)物形狀抽象成直線，零攝氏度處的點(diǎn)抽象成原點(diǎn)，每攝氏度兩條刻度線之間的距離抽象成單位長(zhǎng)度，溫度計(jì)刻度的正、負(fù)度數(shù)分別抽象成相應(yīng)的正數(shù)與負(fù)數(shù)；另一方面，教師要引導(dǎo)學(xué)生將生活實(shí)際問(wèn)題（溫度計(jì)測(cè)溫度過(guò)程）化歸成數(shù)學(xué)問(wèn)題（在數(shù)軸上找出表示相應(yīng)數(shù)的點(diǎn)和將表示數(shù)的點(diǎn)表示在數(shù)軸上）來(lái)研究.同時(shí)在這一過(guò)程中，還要有意識(shí)地滲透一一對(duì)應(yīng)的思想（數(shù)軸上的每一個(gè)點(diǎn)與這個(gè)點(diǎn)所表示的數(shù)之間的關(guān)系）.另外，在相關(guān)習(xí)題的教學(xué)中，要引導(dǎo)學(xué)生充分發(fā)揮數(shù)形結(jié)合的威力，由數(shù)思考點(diǎn)的具體位置，由具體的點(diǎn)考慮它表示哪一個(gè)數(shù)，將數(shù)與形緊密地聯(lián)系起來(lái).又如平面直角坐標(biāo)系，這是由“一維”世界走向“二維”平面的數(shù)學(xué)工具，它在許多實(shí)際問(wèn)題的解決中發(fā)揮了巨大的作用.教學(xué)中教師要有意識(shí)地將這個(gè)工具所蘊(yùn)含的數(shù)學(xué)思想（抽象、數(shù)形結(jié)合、化歸、一一對(duì)應(yīng)、對(duì)稱等）自覺(jué)滲透并應(yīng)用于問(wèn)題解決的全過(guò)程中.因此在理解數(shù)學(xué)的前提下，在對(duì)教材知識(shí)的解讀與研究中，要有意識(shí)地解析感悟出教學(xué)內(nèi)容所蘊(yùn)含的數(shù)學(xué)思想與方法，在理解內(nèi)容所反映的思想方法的基礎(chǔ)上，在教學(xué)中有機(jī)地向?qū)W生進(jìn)行滲透與影響.

二、理解學(xué)生學(xué)情，突出滲透數(shù)學(xué)思想

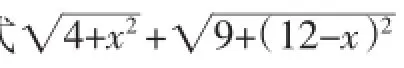
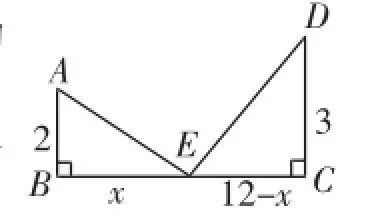
圖1

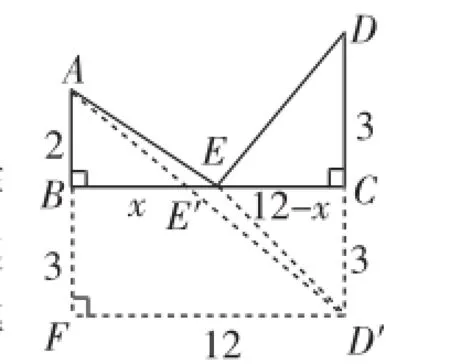
圖2

三、理解教學(xué)實(shí)施，刻意提煉數(shù)學(xué)思想

數(shù)學(xué)思想與方法的教學(xué)是一個(gè)循序漸進(jìn)、日積月累的過(guò)程，它不可能一蹴而就.數(shù)學(xué)思想方法蘊(yùn)含于知識(shí)的發(fā)生、發(fā)展過(guò)程中，數(shù)學(xué)概念和原理的形成過(guò)程是進(jìn)行數(shù)學(xué)思想方法教學(xué)的好載體，沒(méi)有“過(guò)程”就沒(méi)有“思想”.教學(xué)中要注意適時(shí)提出恰當(dāng)?shù)摹?duì)學(xué)生數(shù)學(xué)思維有啟發(fā)的、能充分激發(fā)學(xué)生積極探究的一些好問(wèn)題，讓學(xué)生在問(wèn)題的解決過(guò)程中經(jīng)歷思想方法的滲透與形成過(guò)程.同時(shí)也要充分關(guān)注課堂小結(jié)環(huán)節(jié)，利用課堂點(diǎn)睛這一載體，讓學(xué)生習(xí)得的思想方法納入已有的認(rèn)知系統(tǒng)中.如在“勾股定理”一課教學(xué)中，在定理的猜想環(huán)節(jié)提出：用四張全等的等腰直角三角形紙片拼成正方形，如何由等腰直角三角形的直角邊長(zhǎng)a來(lái)表示正方形（正方形的邊長(zhǎng)為x）的面積？嘗試建立x與a之間的數(shù)量關(guān)系.如何由矩形的一組鄰邊長(zhǎng)a、b來(lái)表示其對(duì)角線長(zhǎng)c？在定理的應(yīng)用鞏固環(huán)節(jié)提出：已知直角三角形兩邊長(zhǎng)分別為3、4，試求斜邊的長(zhǎng).在定理的應(yīng)用拓展環(huán)節(jié)提出：將Rt△ABC的較短直角邊CB繞頂點(diǎn)C按逆時(shí)針（見(jiàn)圖3）或順時(shí)針（見(jiàn)圖4）方向旋轉(zhuǎn)到CB′，連接AB′.仿照勾股定理，試探究邊AB′與邊AC、B′C間的數(shù)量關(guān)系.通過(guò)上述幾問(wèn)的提出與解決，促使學(xué)生從中感悟、體會(huì)聯(lián)想、類比、方程、數(shù)形結(jié)合、分類討論等思想.而在課堂小結(jié)環(huán)節(jié)則以寓樂(lè)于教的編唱歌曲呈現(xiàn)出來(lái).《勾股之歌》：學(xué)習(xí)勾股大定理，尋覓追蹤直角形；面積分割又巧補(bǔ)，探究三邊導(dǎo)關(guān)系；構(gòu)建弦圖巧得證，方法思路人嘆絕；聯(lián)想類比和轉(zhuǎn)化，數(shù)形結(jié)合顯威力；方程建模細(xì)分類，數(shù)學(xué)思想來(lái)引領(lǐng)；究竟勾股多少事，快樂(lè)學(xué)習(xí)無(wú)止境！因此從某種意義上來(lái)說(shuō)，只有理解了教學(xué)，數(shù)學(xué)思想的教學(xué)才成為可能.

數(shù)學(xué)思想是對(duì)數(shù)學(xué)知識(shí)、方法、規(guī)律的一種本質(zhì)性方面的高度概括與提煉，而數(shù)學(xué)知識(shí)則是數(shù)學(xué)思想的載體，它們的內(nèi)涵是極其豐富的.“三個(gè)理解”所承載的教育、教學(xué)功能具有舉足輕重的地位與作用.在日常教學(xué)中，如何在“三個(gè)理解”的視角下更好地創(chuàng)設(shè)有效的教學(xué)載體，將數(shù)學(xué)思想潛移默化地滲透于教學(xué)中，藉以提升學(xué)生的數(shù)學(xué)修養(yǎng)與思想內(nèi)涵，更值得廣大數(shù)學(xué)教師作進(jìn)一步的探索與研究.

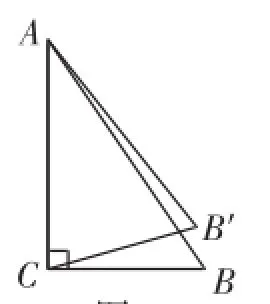
圖3

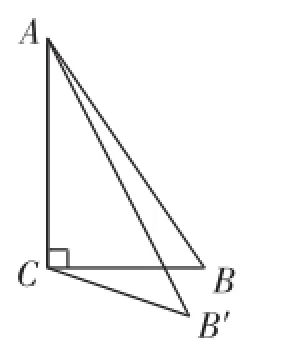
圖4

1.章建躍.理解數(shù)學(xué)理解學(xué)生理解教學(xué)［J］.中國(guó)數(shù)學(xué)教育（高中版），2010（12）.

2.卜以樓.基于“三個(gè)理解”下“圓周角”的教學(xué)預(yù)設(shè)［J］.中學(xué)數(shù)學(xué)（下），2013（11）.

3.酈興江.簡(jiǎn)案3：勾股定理（第1課時(shí)）［J］.中學(xué)數(shù)學(xué)教學(xué)參考（中），2013（11）.WG